科学空间|Scientific Spaces

在《VQ的旋转技巧：梯度直通估计的一般推广》中，我们介绍了VQ（Vector Quantization）的Rotation Trick，它的思想是通过推广VQ的STE（Straight-Through Estimator）来为VQ设计更好的梯度，从而缓解VQ的编码表坍缩、编码表利用率低等问题。

无独有偶，昨天发布在arXiv上的论文《Addressing Representation Collapse in Vector Quantized Models with One Linear Layer》提出了改善VQ的另一个技巧：给编码表加一个线性变换。这个技巧单纯改变了编码表的参数化方式，不改变VQ背后的理论框架，但实测效果非常优异，称得上是简单有效的经典案例。

点击阅读全文...

上一篇文章《当Batch Size增大时，学习率该如何随之变化？》我们从多个角度讨论了学习率与Batch Size之间的缩放规律，其中对于Adam优化器我们采用了SignSGD近似，这是分析Adam优化器常用的手段。那么一个很自然的问题就是：用SignSGD来近似Adam究竟有多科学呢？

我们知道，Adam优化器的更新量分母会带有一个$\epsilon$，初衷是预防除零错误，所以其值通常很接近于零，以至于我们做理论分析的时候通常选择忽略掉它。然而，当前LLM的训练尤其是低精度训练，我们往往会选择偏大的$\epsilon$，这导致在训练的中、后期$\epsilon$往往已经超过梯度平方大小，所以$\epsilon$的存在事实上已经不可忽略。

因此，这篇文章我们试图探索$\epsilon$如何影响Adam的学习率与Batch Size的Scaling Law，为相关问题提供一个参考的计算方案。

点击阅读全文...

随着LLM时代的到来，学术界对于优化器的研究热情似乎有所减退。这主要是因为目前主流的AdamW已经能够满足大多数需求，而如果对优化器“大动干戈”，那么需要巨大的验证成本。因此，当前优化器的变化，多数都只是工业界根据自己的训练经验来对AdamW打的一些小补丁。

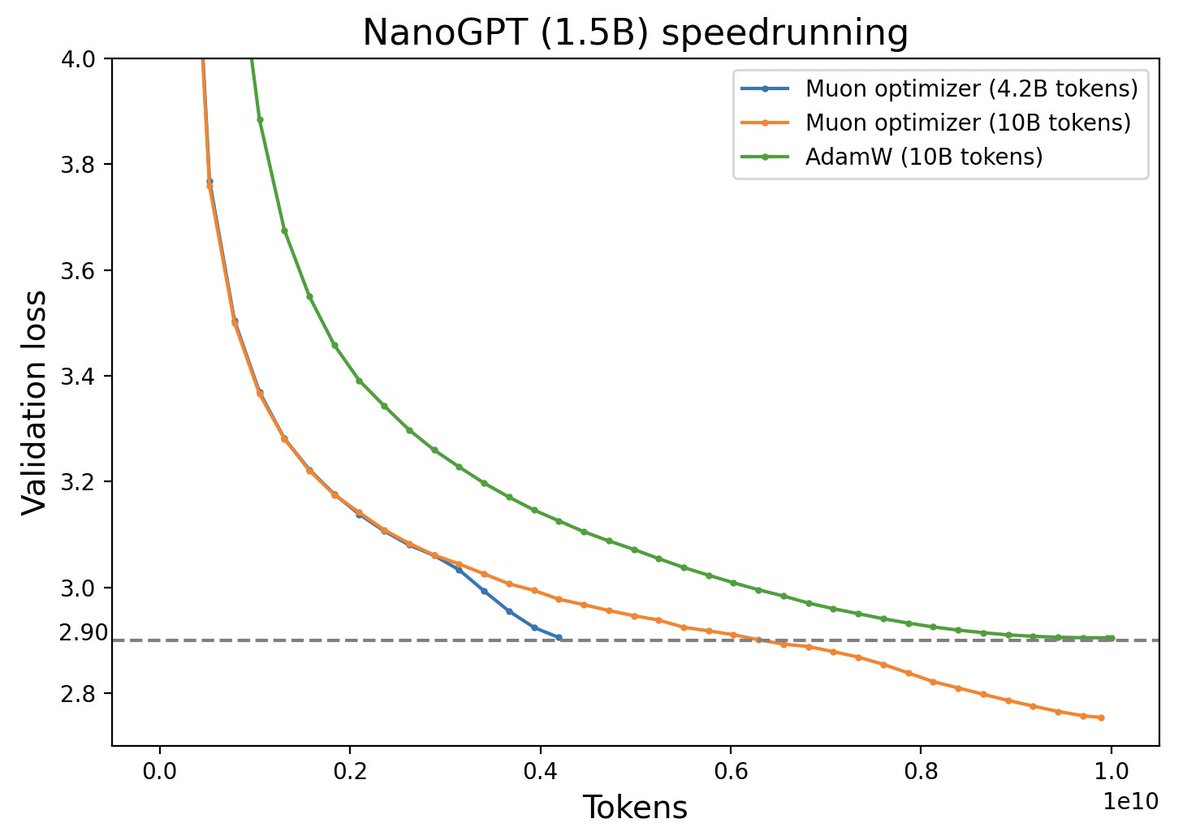
不过，最近推特上一个名为“Muon”的优化器颇为热闹，它声称比AdamW更为高效，且并不只是在Adam基础上的“小打小闹”，而是体现了关于向量与矩阵差异的一些值得深思的原理。本文让我们一起赏析一番。

Muon与AdamW效果对比（来源：推特@Yuchenj_UW）

点击阅读全文...

我们知道，梯度裁剪（Gradient Clipping）是让模型训练更加平稳的常用技巧。常用的梯度裁剪是根据所有参数的梯度总模长来对梯度进行裁剪，其运算可以表示为
\begin{equation}\text{clip}(\boldsymbol{g},\tau)=\left\{\begin{aligned}&\boldsymbol{g}, &\Vert\boldsymbol{g}\Vert\leq \tau \\
&\frac{\tau}{\Vert\boldsymbol{g}\Vert}\boldsymbol{g},&\Vert\boldsymbol{g}\Vert > \tau
\end{aligned}\right.\end{equation}
这样一来，$\text{clip}(\boldsymbol{g},\tau)$保持跟$\boldsymbol{g}$相同的方向，但模长不超过$\tau$。注意这里的$\Vert\boldsymbol{g}\Vert$是整个模型所有的参数梯度放在一起视为单个向量所算的模长，也就是所谓的Global Gradient Norm。

不知道大家有没有留意到一个细节：不管是数百万参数还是数百亿参数的模型，$\tau$的取值在很多时候都是1。这意味着什么呢？是单纯地复用默认值，还是背后隐含着什么深刻的原理呢？

点击阅读全文...

在文章《Muon优化器赏析：从向量到矩阵的本质跨越》中，我们介绍了一个名为“Muon”的新优化器，其中一个理解视角是作为谱范数正则下的最速梯度下降，这似乎揭示了矩阵参数的更本质的优化方向。众所周知，对于矩阵参数我们经常也会加权重衰减（Weight Decay），它可以理解为$F$范数平方的梯度，那么从Muon的视角看，通过谱范数平方的梯度来构建新的权重衰减，会不会能起到更好的效果呢？

那么问题来了，谱范数的梯度或者说导数长啥样呢？用它来设计的新权重衰减又是什么样的？接下来我们围绕这些问题展开。

基础回顾

谱范数（Spectral Norm），又称“$2$范数”，是最常用的矩阵范数之一，相比更简单的$F$范数（Frobenius Norm），它往往能揭示一些与矩阵乘法相关的更本质的信号，这是因为它定义上就跟矩阵乘法相关：对于矩阵参数$\boldsymbol{W}\in\mathbb{R}^{n\times m}$，它的谱范数定义为

点击阅读全文...

氯化氢（HCl），一种无色气体，当它溶于水后变成为了我们常用的盐酸（hydrochloric acid），学名“氢氯酸”。这是一种具有高强度腐蚀性的无机酸，在工业上具有重要的用途。我们胃中的酸也是胃酸。气态的HCl被称为海洋酸性气体。

盐酸是一种一元酸，在水中会发生以下反应：
$$HCl + H_2O=H_3O^+ + Cl^-$$

因此，盐酸可以用来制作其他氯化物（如NaCl）。盐酸是一种强酸，它在水中基本上能够完全解离。

点击阅读全文...

图片说明：酷似鲸鱼和曲棍球棒的星系，版权：Josef Poepsel, Stefan Binnewies&Capella 天文台)

点击阅读全文...

据美国宇航局太空网报道，人类首次登陆月球40周年庆典已经结束，但是美国宇航局能否把人类送上火星仍是一个谜。

休斯顿美国宇航局约翰逊太空中心月球和火星综合研究部研究人员布雷特·德雷克(Bret Drake)说：“目前我们仍把人类探索火星看成是未来的最高目标。人类踏上另一颗行星的风险可能最大，但它也是最有历史纪念意义的事情。”

当前的科技水平可能刚刚达到，也有可能还远远不及前往火星的载人任务所需的技术水平。因此前往这颗红色行星的载人任务仍是一个巨大挑战。但是美国宇航局仍坚持远征火星，而且有关火星探索的新想法层出不穷。德雷克说：“火星是长期以来我们一直向往的地方。”

点击阅读全文...