(原创)切抛物线法解方程
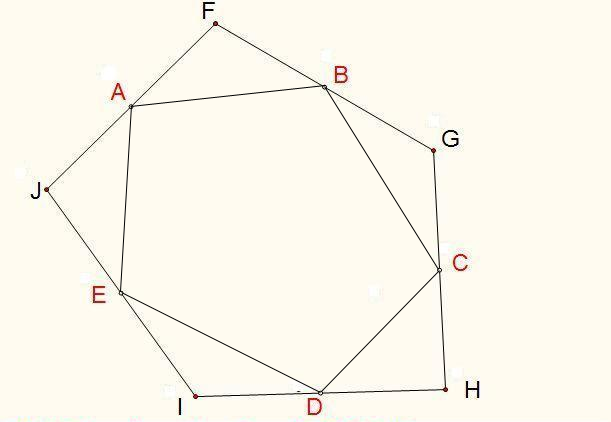
By 苏剑林 | 2010-03-06 | 35729位读者 | 引用已知中心五边形,作五边形
By 苏剑林 | 2010-07-25 | 34874位读者 | 引用外出集训,网站暂停更新...
By 苏剑林 | 2010-07-07 | 33773位读者 | 引用唠叨下,关于三体问题周期轨道
By 苏剑林 | 2011-01-26 | 35134位读者 | 引用我们在研究地球附近的小天体运动时,如果把天体和地球看作一个二体系统,那最多只能算上一个零级近似,如果使用“地球+月球+小天体”组成的圆形限制性三体问题模型,那可以算上一个二级近似了。那么,一级近似又是什么了。BoJone认为,它就是本文将要讲的“双固定引力中心问题”了,也叫“双不动中心问题”,英文名是two fixed-center problem。这是一种特殊的限制性三体问题。在这个三体系统中,两个主天体(或称有限质量天体)固定不动,第三个小天体在两个固定的主天体吸引下运动。欧拉、拉格朗日、勒让德、雅可比等人很早就研究过这个问题。其中,欧拉最先成功地求出了这个系统的积分。[引用]
另外,双固定引力中心问题还有另外一个应用,在研究人造卫星的运动时,可以只考虑地球引力,但是由于地球不是完美的球体,把其看成一个质点其实不十分精确,要是把它拆分为两个引力源,就可以很大程度上提高精确度。毕竟双固定引力中心问题是完全可以积分的,可以作为一个比较好的中间轨道(介乎圆锥曲线和精确轨道之间的)。
看完了“双不动中心”问题,我们不妨再来看一个貌似简单一点的力学问题,在一个固定质点的引力吸引的基础上,增加一个恒力作用,研究这样的力场中小天体的运动。
咋看上去这个问题比“双不动中心”简单多了,至少运动方程也显得更简单:
¨vecr=−GM→r|→r|3+→F
其中→F是一个常向量。不过让人比较意外的是,这个问题本质上和“双不动中心”是一样的,它可以看作是双不动中心问题的一个极限情况。而且它们的解法也是惊人地相似,下面我们就来分析这一个过程。
首先很容易写出这个方程的能量守恒积分:
1/2˙vecr2−GM1|→r|−→F⋅→r=h









最近评论