24
Apr
用RecomposIt简单给图片换背景
By 苏剑林 | 2010-04-24 | 29740位读者 | 引用
17
Apr
Lamost被冠名为“郭守敬望远镜”
By 苏剑林 | 2010-04-17 | 57930位读者 | 引用
9
Feb
【NASA每日一图】夜晚发射的“奋进号”
By 苏剑林 | 2010-02-09 | 19794位读者 | 引用
14
May
奔向固原,追逐梦想...
By 苏剑林 | 2010-05-14 | 56799位读者 | 引用
25
Jul
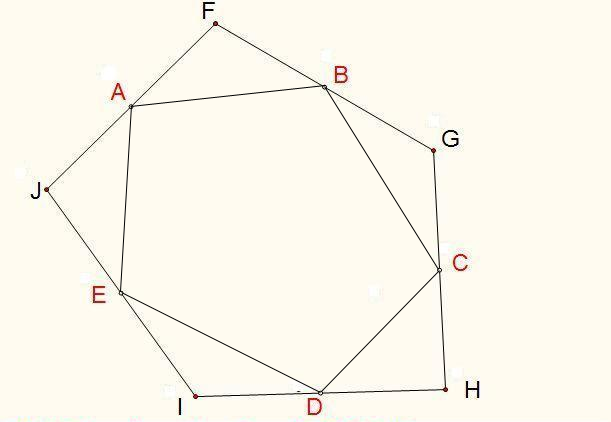
已知中心五边形,作五边形
By 苏剑林 | 2010-07-25 | 35210位读者 | 引用
26
Jun
再次错过了“食”...
By 苏剑林 | 2010-06-26 | 32796位读者 | 引用
15
Jul
《向量》系列——1.向心力公式证明
By 苏剑林 | 2010-07-15 | 64232位读者 | 引用向量在几何和物理中都有极其重要的作用,现在就让我们来看如何用向量研究物理中的圆周运动。
首先我们必须了解一些基础:
1.在向量中,只要一条“向径”(→r)就可以描述出物体的运动,而不需要建立坐标系。这就是向量应用于物理的原因:物理定律不应该依赖于坐标系,而向量恰恰也不依赖于坐标系!
2.牛顿第二定律:→F=m→a
3.以及一些向量的微积分运算等(可以查阅维基百科或者相关资料)
在下面及以后的文章描述中,为了大家的阅读方便,把向量写成→r的形式,而非把字母加粗。一般情况下,在本站的描述中,有|→r|=r,|˙→r|=v,|¨→r|=a。但是,˙r=d|→r|dt!=|˙→r|
24
Jul













最近评论