AdaX优化器浅析(附开源实现)
By 苏剑林 | 2020-05-11 | 44386位读者 | Kimi 引用这篇文章简单介绍一个叫做AdaX的优化器,来自《AdaX: Adaptive Gradient Descent with Exponential Long Term Memory》。介绍这个优化器的原因是它再次印证了之前在《AdaFactor优化器浅析(附开源实现)》一文中提到的一个结论,两篇文章可以对比着阅读。
Adam & AdaX
AdaX的更新格式是
\begin{equation}\left\{\begin{aligned}&g_t = \nabla_{\theta} L(\theta_t)\\
&m_t = \beta_1 m_{t-1} + \left(1 - \beta_1\right) g_t\\
&v_t = (1 + \beta_2) v_{t-1} + \beta_2 g_t^2\\
&\hat{v}_t = v_t\left/\left(\left(1 + \beta_2\right)^t - 1\right)\right.\\
&\theta_t = \theta_{t-1} - \alpha_t m_t\left/\sqrt{\hat{v}_t + \epsilon}\right.
\end{aligned}\right.\end{equation}
其中$\beta_2$的默认值是$0.0001$。对了,顺便附上自己的Keras实现:https://github.com/bojone/adax
变分自编码器(五):VAE + BN = 更好的VAE
By 苏剑林 | 2020-05-06 | 297020位读者 | Kimi 引用本文我们继续之前的变分自编码器系列,分析一下如何防止NLP中的VAE模型出现“KL散度消失(KL Vanishing)”现象。本文受到参考文献是ACL 2020的论文《A Batch Normalized Inference Network Keeps the KL Vanishing Away》的启发,并自行做了进一步的完善。
值得一提的是,本文最后得到的方案还是颇为简洁的——只需往编码输出加入BN(Batch Normalization),然后加个简单的scale——但确实很有效,因此值得正在研究相关问题的读者一试。同时,相关结论也适用于一般的VAE模型(包括CV的),如果按照笔者的看法,它甚至可以作为VAE模型的“标配”。
最后,要提醒读者这算是一篇VAE的进阶论文,所以请读者对VAE有一定了解后再来阅读本文。
VAE简单回顾
这里我们简单回顾一下VAE模型,并且讨论一下VAE在NLP中所遇到的困难。关于VAE的更详细介绍,请读者参考笔者的旧作《变分自编码器(一):原来是这么一回事》、《变分自编码器(二):从贝叶斯观点出发》等。
VAE的训练流程
VAE的训练流程大概可以图示为
节省显存的重计算技巧也有了Keras版了
By 苏剑林 | 2020-04-29 | 62401位读者 | Kimi 引用不少读者最近可能留意到了公众号文章《BERT重计算:用22.5%的训练时间节省5倍的显存开销(附代码)》,里边介绍了一个叫做“重计算”的技巧,简单来说就是用来省显存的方法,让平均训练速度慢一点,但batch_size可以增大好几倍。该技巧首先发布于论文《Training Deep Nets with Sublinear Memory Cost》,其实在2016年就已经提出了,只不过似乎还没有特别流行起来。
探索
公众号文章提到该技巧在pytorch和paddlepaddle都有原生实现了,但tensorflow还没有。但事实上从tensorflow 1.8开始,tensorflow就已经自带了该功能了,当时被列入了tf.contrib这个子库中,而从tensorflow 1.15开始,它就被内置为tensorflow的主函数之一,那就是tf.recompute_grad。
找到tf.recompute_grad之后,笔者就琢磨了一下它的用法,经过一番折腾,最终居然真的成功地用起来了,居然成功地让batch_size从48增加到了144!然而,在继续整理测试的过程中,发现这玩意居然在tensorflow 2.x是失效的...于是再折腾了两天,查找了各种资料并反复调试,最终算是成功地补充了这一缺陷。
最后是笔者自己的开源实现:
该实现已经内置在bert4keras中,使用bert4keras的读者可以升级到最新版本(0.7.5+)来测试该功能。
将“Softmax+交叉熵”推广到多标签分类问题
By 苏剑林 | 2020-04-25 | 499912位读者 | Kimi 引用(注:本文的相关内容已整理成论文《ZLPR: A Novel Loss for Multi-label Classification》,如需引用可以直接引用英文论文,谢谢。)
一般来说,在处理常规的多分类问题时,我们会在模型的最后用一个全连接层输出每个类的分数,然后用softmax激活并用交叉熵作为损失函数。在这篇文章里,我们尝试将“Softmax+交叉熵”方案推广到多标签分类场景,希望能得到用于多标签分类任务的、不需要特别调整类权重和阈值的loss。
单标签到多标签
一般来说,多分类问题指的就是单标签分类问题,即从$n$个候选类别中选$1$个目标类别。假设各个类的得分分别为$s_1,s_2,
\dots,s_n$,目标类为$t\in\{1,2,\dots,n\}$,那么所用的loss为
\begin{equation}-\log \frac{e^{s_t}}{\sum\limits_{i=1}^n e^{s_i}}= - s_t + \log \sum\limits_{i=1}^n e^{s_i}\label{eq:log-softmax}\end{equation}
这个loss的优化方向是让目标类的得分$s_t$变为$s_1,s_2,\dots,s_t$中的最大值。关于softmax的相关内容,还可以参考《寻求一个光滑的最大值函数》、《函数光滑化杂谈:不可导函数的可导逼近》等文章。
EAE:自编码器 + BN + 最大熵 = 生成模型
By 苏剑林 | 2020-04-20 | 79381位读者 | Kimi 引用生成模型一直是笔者比较关注的主题,不管是NLP和CV的生成模型都是如此。这篇文章里,我们介绍一个新颖的生成模型,来自论文《Batch norm with entropic regularization turns deterministic autoencoders into generative models》,论文中称之为EAE(Entropic AutoEncoder)。它要做的事情给变分自编码器(VAE)基本一致,最终效果其实也差不多(略优),说它新颖并不是它生成效果有多好,而是思路上的新奇,颇有别致感。此外,借着这个机会,我们还将学习一种统计量的估计方法——$k$邻近方法,这是一种很有用的非参数估计方法。
自编码器vs生成模型
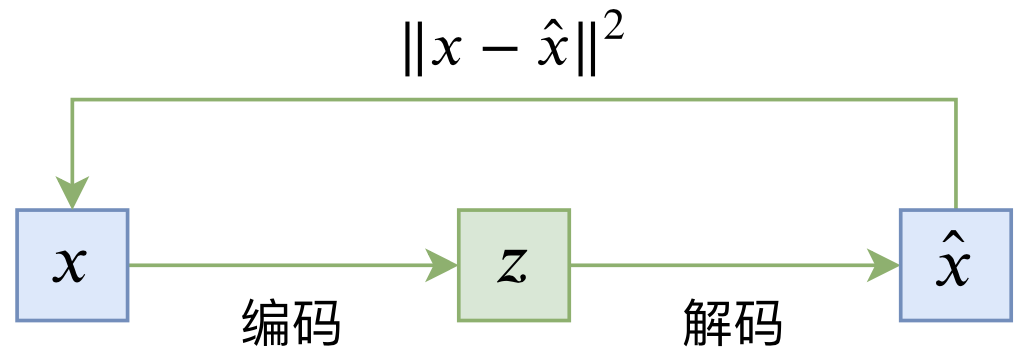
普通的自编码器是一个“编码-解码”的重构过程,如下图所示:
其loss一般为
\begin{equation}L_{AE} = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - \hat{x}\right\Vert^2\right] = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - D(E(x))\right\Vert^2\right]\end{equation}
突破瓶颈,打造更强大的Transformer
By 苏剑林 | 2020-04-13 | 191314位读者 | Kimi 引用自《Attention is All You Need》一文发布后,基于Multi-Head Attention的Transformer模型开始流行起来,而去年发布的BERT模型更是将Transformer模型的热度推上了又一个高峰。当然,技术的探索是无止境的,改进的工作也相继涌现:有改进预训练任务的,比如XLNET的PLM、ALBERT的SOP等;有改进归一化的,比如Post-Norm向Pre-Norm的改变,以及T5中去掉了Layer Norm里边的beta参数等;也有改进模型结构的,比如Transformer-XL等;有改进训练方式的,比如ALBERT的参数共享等;...
以上的这些改动,都是在Attention外部进行改动的,也就是说它们都默认了Attention的合理性,没有对Attention本身进行改动。而本文我们则介绍关于两个新结果:它们针对Multi-Head Attention中可能存在建模瓶颈,提出了不同的方案来改进Multi-Head Attention。两篇论文都来自Google,并且做了相当充分的实验,因此结果应该是相当有说服力的了。
再小也不能小key_size
第一个结果来自文章《Low-Rank Bottleneck in Multi-head Attention Models》,它明确地指出了Multi-Head Attention里边的表达能力瓶颈,并提出通过增大key_size的方法来缓解这个瓶颈。
bert4keras在手,baseline我有:百度LIC2020
By 苏剑林 | 2020-04-02 | 127301位读者 | Kimi 引用百度的“2020语言与智能技术竞赛”开赛了,今年有五个赛道,分别是机器阅读理解、推荐任务对话、语义解析、关系抽取、事件抽取。每个赛道中,主办方都给出了基于PaddlePaddle的baseline模型,这里笔者也基于bert4keras给出其中三个赛道的个人baseline,从中我们可以看到用bert4keras搭建baseline模型的方便快捷与简练。
思路简析
这里简单分析一下这三个赛道的任务特点以及对应的baseline设计。
GELU的两个初等函数近似是怎么来的
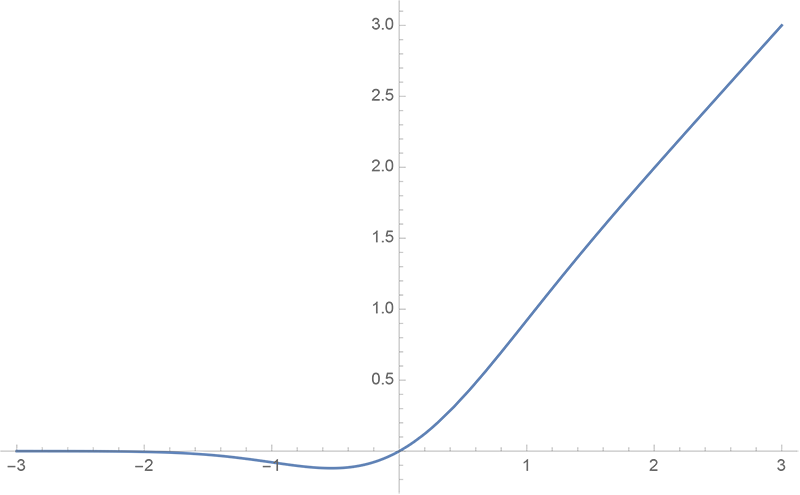
By 苏剑林 | 2020-03-26 | 80164位读者 | Kimi 引用GELU,全称为Gaussian Error Linear Unit,也算是RELU的变种,是一个非初等函数形式的激活函数。它由论文《Gaussian Error Linear Units (GELUs)》提出,后来被用到了GPT中,再后来被用在了BERT中,再再后来的不少预训练语言模型也跟着用到了它。随着BERT等预训练语言模型的兴起,GELU也跟着水涨船高,莫名其妙地就成了热门的激活函数了。
在GELU的原始论文中,作者不仅提出了GELU的精确形式,还给出了两个初等函数的近似形式,本文来讨论它们是怎么得到的。







 感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持!
感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持! 科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。
科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。 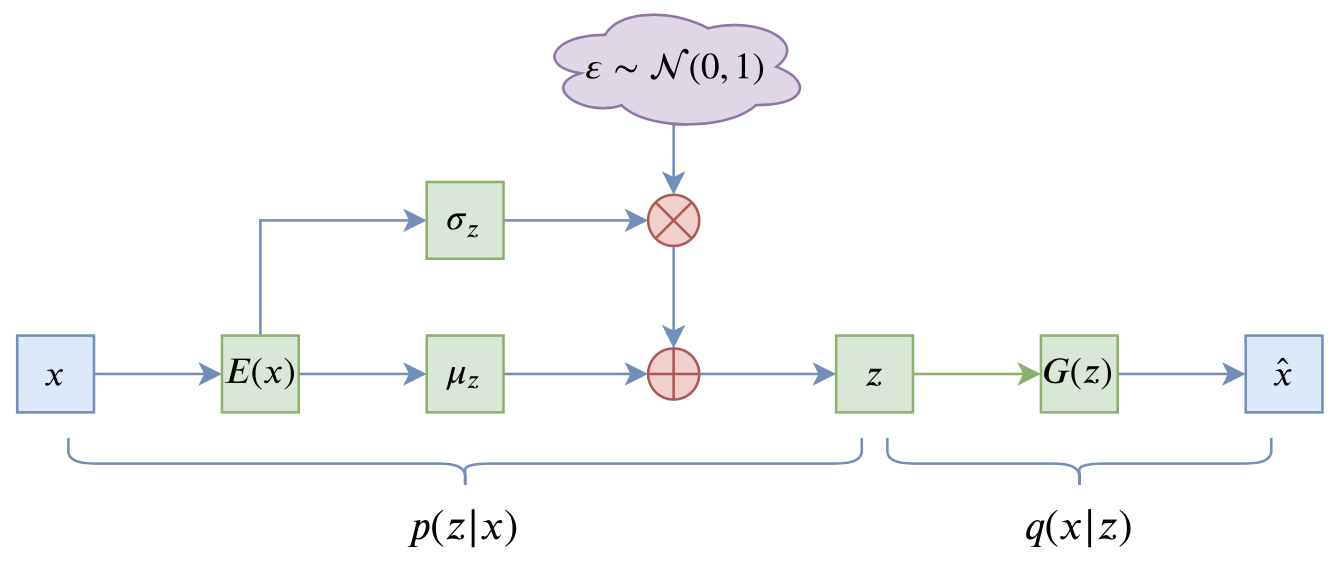


最近评论