两个惊艳的python库:tqdm和retry
By 苏剑林 | 2016-08-13 | 79957位读者 | 引用Python基本是我目前工作、计算、数据挖掘的唯一编程语言(除了符号计算用Mathematica外)。当然,基本的Python功能并不是很强大,但它胜在有巨量的第三方扩展库。在选用Python的第三方库时,我都会经过仔细考虑,希望能挑选出最简单的、最直观的一个(因为本人比较笨,太复杂用不了)。在数据处理方面,我用得最多的是Numpy和Pandas,这两个绝对称得上王者级别的库,当然不能不提的是Scipy,但我很少直接用它,一般会通过Pandas间接调用了;可视化方面不用说是Matplotlib了;在建模方面,我会用Keras,直接上深度学习模型,Keras已经成为相当流行的深度学习框架了,如果做文本挖掘,通常还会用到jieba(分词)、Gensim(主题建模,包含了诸如word2vec之类的模型),机器学习库还有流行的Scikit Learn,但我很少用;网络方面,写爬虫我用requests,这是个人性化的网络库,如果写网站,我会用bottle,这是个单文件版的迷你框架,一切由自己定义,当然,我也不会去写什么大型网站,我就写一个简单的的接口那样而已;最后如果要并行的话,一般直接用multiprocessing。
不过,以上都不是本文要推荐的,本文要推荐的是两个可以渗透到日常写代码的库,它实现了我们平时很多时候都需要的功能,但是不用增加什么代码,绝对让人眼前一亮。
最近一直在考虑一些自然语言处理问题和一些非线性分析问题,无暇总结发文,在此表示抱歉。本文要说的是对于一阶非线性差分方程(当然高阶也可以类似地做)的一种摄动格式,理论上来说,本方法可以得到任意一阶非线性差分方程的显式渐近解。
非线性差分方程
对于一般的一阶非线性差分方程
$$\begin{equation}\label{chafenfangcheng}x_{n+1}-x_n = f(x_n)\end{equation}$$
通常来说,差分方程很少有解析解,因此要通过渐近分析等手段来分析非线性差分方程的性质。很多时候,我们首先会考虑将差分替换为求导,得到微分方程
$$\begin{equation}\label{weifenfangcheng}\frac{dx}{dn}=f(x)\end{equation}$$
作为差分方程$\eqref{chafenfangcheng}$的近似。其中的原因,除了微分方程有比较简单的显式解之外,另一重要原因是微分方程$\eqref{weifenfangcheng}$近似保留了差分方程$\eqref{chafenfangcheng}$的一些比较重要的性质,如渐近性。例如,考虑离散的阻滞增长模型:
$$\begin{equation}\label{zuzhizengzhang}x_{n+1}=(1+\alpha)x_n -\beta x_n^2\end{equation}$$
对应的微分方程为(差分替换为求导):
$$\begin{equation}\frac{dx}{dn}=\alpha x -\beta x^2\end{equation}$$
此方程解得
$$\begin{equation}x_n = \frac{\alpha}{\beta+c e^{-\alpha n}}\end{equation}$$
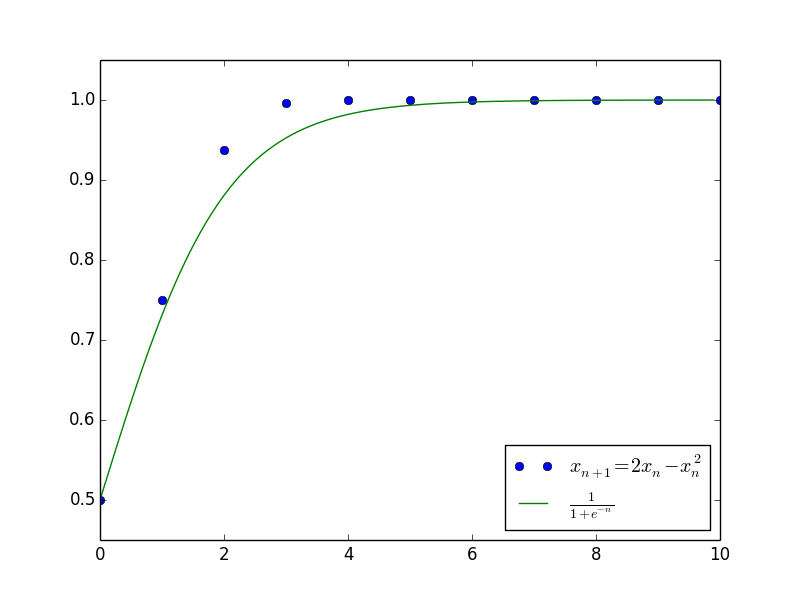
其中$c$是任意常数。上述结果已经大概给出了原差分方程$\eqref{zuzhizengzhang}$的解的变化趋势,并且成功给出了最终的渐近极限$x_n \to \frac{\alpha}{\beta}$。下图是当$\alpha=\beta=1$且$c=1$(即$x_0=\frac{1}{2}$)时,微分方程的解与差分方程的解的值比较。
现在的问题是,既然微分方程的解可以作为一个形态良好的近似解了,那么是否可以在微分方程的解的基础上,进一步加入修正项提高精度?
运动相机测试:家乡的星空
By 苏剑林 | 2016-08-03 | 45829位读者 | 引用记得很早之前就想尝试一下拍星空,无奈一直都没有设备。以前只知道单反可以拍星空,因此,一直以来的想法就是有钱了就去买台单反。因为各种原因一拖再拖,最后慢慢觉得,对于我这种三分钟热度的人来说,单反的意义还真的不是很大。
这两年,在小米的鼓吹下,小蚁运动相机在国内算是慢慢掀起了一股运动相机潮。这种相机的特点是小巧、灵活,价格也不贵(相比单反)。灵活不仅仅是说它便于携带,而且还是功能上的灵活,比如一代小蚁还支持编程拍摄!(写程序控制快门、ISO、拍摄间隔,并实现定时拍摄等)这样当然很快就吸引了我,在小蚁2代众筹之时,我也咬咬牙,入了一台。
前两天回到家,刚好晴夜,马上就试了一下拍星空的效果。下面是在我家楼顶拍的,用ISO400曝光30秒的效果:
从Boosting学习到神经网络:看山是山?
By 苏剑林 | 2016-07-01 | 88524位读者 | 引用前段时间在潮州给韩师的同学讲文本挖掘之余,涉猎到了Boosting学习算法,并且做了一番头脑风暴,最后把Boosting学习算法的一些本质特征思考清楚了,而且得到一些意外的结果,比如说AdaBoost算法的一些理论证明也可以用来解释神经网络模型这么强大。
AdaBoost算法
Boosting学习,属于组合模型的范畴,当然,与其说它是一个算法,倒不如说是一种解决问题的思路。以有监督的分类问题为例,它说的是可以把弱的分类器(只要准确率严格大于随机分类器)通过某种方式组合起来,就可以得到一个很优秀的分类器(理论上准确率可以100%)。AdaBoost算法是Boosting算法的一个例子,由Schapire在1996年提出,它构造了一种Boosting学习的明确的方案,并且从理论上给出了关于错误率的证明。
以二分类问题为例子,假设我们有一批样本$\{x_i,y_i\},i=1,2,\dots,n$,其中$x_i$是样本数据,有可能是多维度的输入,$y_i\in\{1,-1\}$为样本标签,这里用1和-1来描述样本标签而不是之前惯用的1和0,只是为了后面证明上的方便,没有什么特殊的含义。接着假设我们已经有了一个弱分类器$G(x)$,比如逻辑回归、SVM、决策树等,对分类器的唯一要求是它的准确率要严格大于随机(在二分类问题中就是要严格大于0.5),所谓严格大于,就是存在一个大于0的常数$\epsilon$,每次的准确率都不低于$\frac{1}{2}+\epsilon$。
文本情感分类(三):分词 OR 不分词
By 苏剑林 | 2016-06-29 | 520362位读者 | 引用去年泰迪杯竞赛过后,笔者写了一篇简要介绍深度学习在情感分析中的应用的博文《文本情感分类(二):深度学习模型》。虽然文章很粗糙,但还是得到了不少读者的反响,让我颇为意外。然而,那篇文章中在实现上有些不清楚的地方,这是因为:1、在那篇文章以后,keras已经做了比较大的改动,原来的代码不通用了;2、里边的代码可能经过我随手改动过,所以发出来的时候不是最适当的版本。因此,在近一年之后,我再重拾这个话题,并且完成一些之前没有完成的测试。
为什么要用深度学习模型?除了它更高精度等原因之外,还有一个重要原因,那就是它是目前唯一的能够实现“端到端”的模型。所谓“端到端”,就是能够直接将原始数据和标签输入,然后让模型自己完成一切过程——包括特征的提取、模型的学习。而回顾我们做中文情感分类的过程,一般都是“分词——词向量——句向量(LSTM)——分类”这么几个步骤。虽然很多时候这种模型已经达到了state of art的效果,但是有些疑问还是需要进一步测试解决的。对于中文来说,字才是最低粒度的文字单位,因此从“端到端”的角度来看,应该将直接将句子以字的方式进行输入,而不是先将句子分好词。那到底有没有分词的必要性呢?本文测试比较了字one hot、字向量、词向量三者之间的效果。
模型测试
本文测试了三个模型,或者说,是三套框架,具体代码在文末给出。这三套框架分别是:
1、one hot:以字为单位,不分词,将每个句子截断为200字(不够则补空字符串),然后将句子以“字-one hot”的矩阵形式输入到LSTM模型中进行学习分类;
2、one embedding:以字为单位,不分词,,将每个句子截断为200字(不够则补空字符串),然后将句子以“字-字向量(embedding)“的矩阵形式输入到LSTM模型中进行学习分类;
3、word embedding:以词为单位,分词,,将每个句子截断为100词(不够则补空字符串),然后将句子以“词-词向量(embedding)”的矩阵形式输入到LSTM模型中进行学习分类。
OCR技术浅探:9. 代码共享(完)
By 苏剑林 | 2016-06-26 | 89314位读者 | 引用OCR技术浅探:8. 综合评估
By 苏剑林 | 2016-06-26 | 36374位读者 | 引用数据验证
尽管在测试环境下模型工作良好,但是实践是检验真理的唯一标准. 在本节中,我们通过自己的模型,与京东的测试数据进行比较验证.
衡量OCR系统的好坏有两部分内容:(1)是否成功地圈出了文字;(2)对于圈出来的文字,有没有成功识别. 我们采用评分的方法,对每一张图片的识别效果进行评分. 评分规则如下:
如果圈出的文字区域能够跟京东提供的检测样本的box文件中匹配,那么加1分,如果正确识别出文字来,另外加1分,最后每张图片的分数是前面总分除以文字总数.
按照这个规则,每张图片的评分最多是2分,最少是0分. 如果评分超过1,说明识别效果比较好了. 经过京东的测试数据比较,我们的模型平均评分大约是0.84,效果差强人意。
OCR技术浅探:7. 语言模型
By 苏剑林 | 2016-06-26 | 63186位读者 | 引用由于图像质量等原因,性能再好的识别模型,都会有识别错误的可能性,为了减少识别错误率,可以将识别问题跟统计语言模型结合起来,通过动态规划的方法给出最优的识别结果.这是改进OCR识别效果的重要方法之一.
转移概率
在我们分析实验结果的过程中,有出现这一案例.由于图像不清晰等可能的原因,导致“电视”一词被识别为“电柳”,仅用图像模型是不能很好地解决这个问题的,因为从图像模型来看,识别为“电柳”是最优的选择.但是语言模型却可以很巧妙地解决这个问题.原因很简单,基于大量的文本数据我们可以统计“电视”一词和“电柳”一词的概率,可以发现“电视”一词的概率远远大于“电柳”,因此我们会认为这个词是“电视”而不是“电柳”.
从概率的角度来看,就是对于第一个字的区域的识别结果$s_1$,我们前面的卷积神经网络给出了“电”、“宙”两个候选字(仅仅选了前两个,后面的概率太小),每个候选字的概率$W(s_1)$分别为0.99996、0.00004;第二个字的区域的识别结果$s_2$,我们前面的卷积神经网络给出了“柳”、“视”、“规”(仅仅选了前三个,后面的概率太小),每个候选字的概率$W(s_2)$分别为0.87838、0.12148、0.00012,因此,它们事实上有六种组合:“电柳”、“电视”、“电规”、“宙柳”、“宙视”、“宙规”.









最近评论