“熵”不起：从熵、最大熵原理到最大熵模型（二）

上集回顾 #

在第一篇中，笔者介绍了“熵”这个概念，以及它的一些来龙去脉。熵的公式为
$$S=-\sum_x p(x)\log p(x)\tag{1}$$
或
$$S=-\int p(x)\log p(x) dx\tag{2}$$
并且在第一篇中，我们知道熵既代表了不确定性，又代表了信息量，事实上它们是同一个概念。

说完了熵这个概念，接下来要说的是“最大熵原理”。最大熵原理告诉我们，当我们想要得到一个随机事件的概率分布时，如果没有足够的信息能够完全确定这个概率分布（可能是不能确定什么分布，也可能是知道分布的类型，但是还有若干个参数没确定），那么最为“保险”的方案是选择使得熵最大的分布。

最大熵原理 #

承认我们的无知 #

很多文章在介绍最大熵原理的时候，会引用一句著名的句子——“不要把鸡蛋放在同一个篮子里”——来通俗地解释这个原理。然而，笔者窃以为这句话并没有抓住要点，并不能很好地体现最大熵原理的要义。笔者认为，对最大熵原理更恰当的解释是：承认我们的无知！

如何理解这句话跟最大熵原理的联系呢？我们已经知道，熵是不确定性的度量，最大熵，意味着最大的不确定性，那么很显然，我们要选取熵最大的分布，也就意味着我们选择了我们对它最无知的分布。换言之，承认我们对问题的无知，不要自欺欺人，也许我们可以相互欺骗，但是我们永远也欺骗不了大自然。

举例来说，抛一枚硬币，我们一般会认为正反两面的概率是一样的，这时候熵最大，我们对这个硬币处于最无知的状态；假如有一个人，很自信正面向上的概率是60%，反面是40%，那么他肯定是知道了硬币做过手脚，使得正面向上的概率大一些。因此，那个人对硬币的了解程度肯定比我们要高，而我们如果不了解这个信息，那么还是老老实实地承认我们的无知，只好认为正反面概率一样，不要做主观臆测（因为可以主观臆测的东西太多了，如果我们错误地认为反面的概率更高，那么将会使得我们更加血本无归。）

因此，选取熵最大的模型，意味着我们对自然的坦诚，而我们相信我们对自然坦诚了，自然也不会亏待我们。这边是最大熵原理的哲学意义所在。另外，承认我们的无知，也就意味着我们假设能从中获得最大的信息量，这在某种意义上，也符合最经济的法则。

估算概率 #

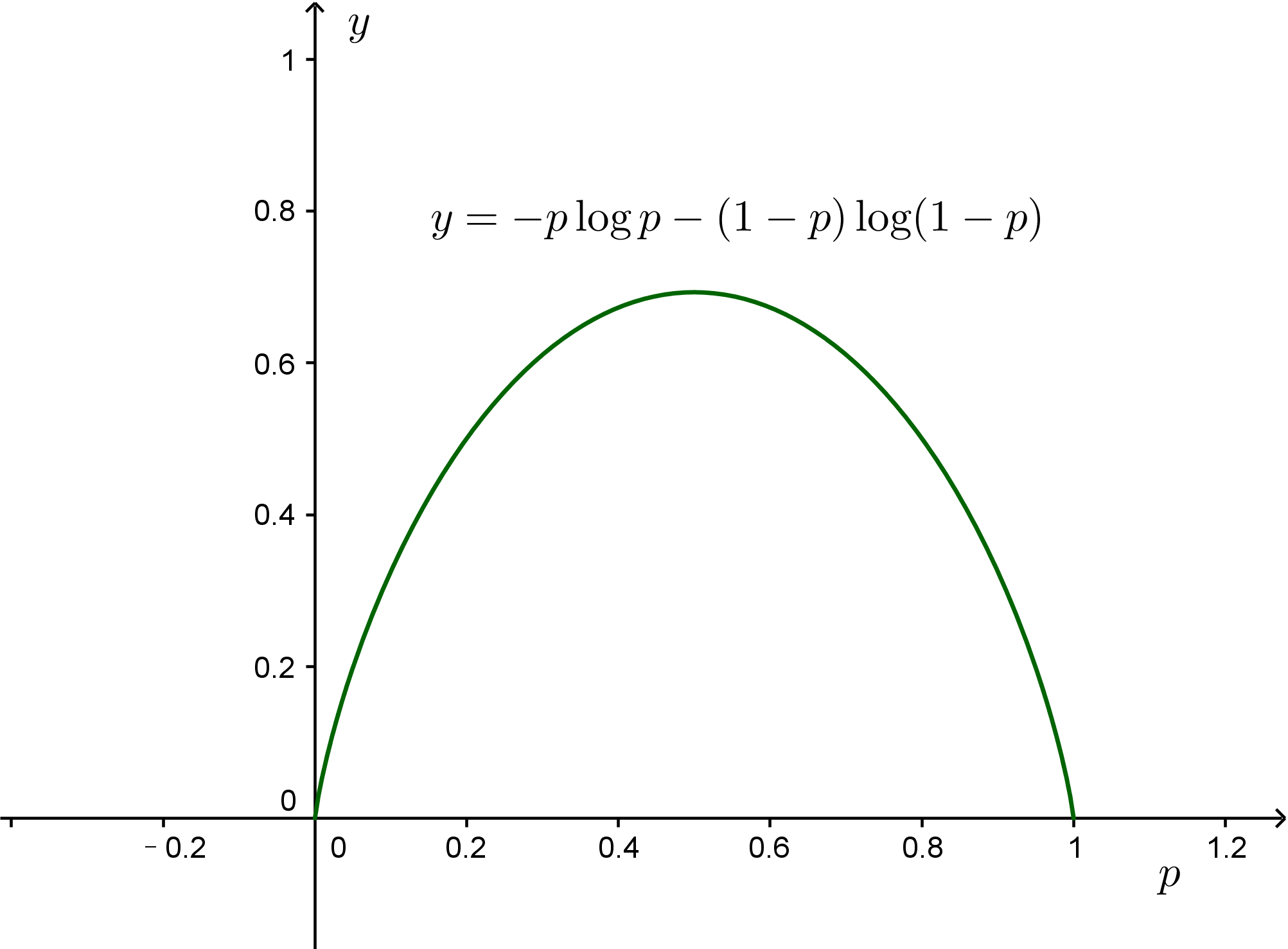
说了那么多，还没有真正动手算些什么，显然单靠文字是很难有说服力的。首先，我们来解决最简单的一个问题，根据最大熵原理说明为什么我们认为抛硬币时，正负两面的概率都是$\frac{1}{2}$。假设正面的概率为$p$，则熵为
$$S(p) = -p \log p - (1-p)\log (1-p)\tag{15}$$
求导可以算得，当$p=\frac{1}{2}$时，$S(p)$最大，所以我们猜测每个面的概率都是$\frac{1}{2}$。类似地，可以证明，根据最大熵原理得抛骰子的时候，每个面的概率应该是$\frac{1}{6}$，这是一个多元微积分的问题；如果有$n$种可能性，每种可能性的概率的概率应该是$\frac{1}{n}$。

最大熵原理

要注意，以上都是假设我们是完全无知的情况下作出的估计。事实上，很多时候我们并没有那么无知，我们可以根据大量的统计，得出一些信息，来完善我们的认识。比如下面的例子：

一个快餐店提供3种食品：汉堡(1)、鸡肉(2)、鱼(3)。价格分别是1元、2元、3元。已知人们在这家店的平均消费是1.75元，求顾客购买这3种食品的概率。

这里“人们在这家店的平均消费是1.75元”就是我们根据大量统计得到的一个结果。如果我们假设我们是完全无知的，那么就得到购买每种食物的概率是$\frac{1}{3}$，但是这样平均消费应该是2元，并不符合“人们在这家店的平均消费是1.75元”这个事实。换言之，我们对这个快餐店的购买情况并不至于完全无知，至少我们知道了“人们在这家店的平均消费是1.75元”，这个事实有助于我们更准确地估计概率。

估计框架 #

离散型概率 #

这些有助于我们更准确估计概率的“事实”，有可能是我们的生活经验，也有可能是某种先验信息，但是不管怎样，它必然是统计出来的结果，数学的描述就是以期望形式给出的约束：
$$E[f(x)]=\sum_{x} p(x)f(x) = \tau\tag{16}$$
要注意，虽然现在我们并不至于完全无知，但是我们还是得承认自己是无知的，这种无知，实在已知一些事实的前提下的无知。用数学的语言说，就是现在问题变成了，在$k$个形如$(16)$式的约束之下，求$(1)$式的最大值。对于快餐店的例子，$f(x)=x$，即
$$\sum_{x=1,2,3}p(x)x=1.75\tag{17}$$
求$-\sum_x p(x)\log p(x)$的最大值。这种题目其实就是微积分中的带有约束的极值问题，方法就是拉格朗日乘子法，即引入参数$\lambda$，那么原问题等价于求下式的极值
$$-\sum_x p(x)\log p(x)-\lambda_0\left(\sum_x p(x) -1\right)-\lambda_1\left(\sum_x p(x)x -1.75\right)\tag{18}$$
在$(18)$式中，我们引入了两个约束，第一个约束是通用的，即所有$p(x)$之和为1；第二个就是我们所认识到的“事实”。求导解得极值点为$p(1) = 0.466,p(2) = 0.318,p(3)=0.216$，这时候熵最大。

更一般地，假设有$k$个约束，那么就要求以下问题的极值：
$$\begin{aligned}-\sum_x p(x)\log p(x)&-\lambda_0\left(\sum_x p(x) -1\right)-\lambda_1\left(\sum_x p(x)f_1(x) -\tau_1\right)\\
&-\dots-\lambda_k\left(\sum_x p(x)f_k(x) -\tau_k\right)\end{aligned}\tag{19}$$
$(19)$式容易解得
$$p(x)=\frac{1}{Z}\exp\left(-\sum_{i=1}^k \lambda_i f_i (x)\right)\tag{20}$$
这里的$Z$是归一化因子，即
$$Z=\sum_x \exp\left(-\sum_{i=1}^k \lambda_i f_i (x)\right)\tag{21}$$
将$(20)$式代入
$$\sum_x p(x)f_i(x) -\tau_i=0,\quad (i=1,2,\dots,k)\tag{22}$$
就可以解出各个未知的$\lambda_i$（遗憾的是，对于一般的$f_i(x)$，上式并没有简单解，甚至数值求解都不容易，这使得最大熵相关的模型都比较难使用。）

连续型概率 #

要注意，$(19),(20),(21),(22)$式是基于离散型概率推导的结果，连续型概率的结果类似，如$(19)$式对应于
$$\begin{aligned}-\int p(x)\log p(x)dx &-\lambda_0\left(\int p(x)dx -1\right)-\lambda_1\left(\int p(x)f_1(x)dx -\tau_1\right)\\
&-\dots-\lambda_k\left(\int p(x)f_k(x)dx -\tau_k\right)\end{aligned}\tag{23}$$
求$(23)$式的最大值事实上是一个变分问题，但是由于没有出现导数项，因此这个变分问题跟普通的求导没有多大区别，结果仍是
$$p(x)=\frac{1}{Z}\exp\left(-\sum_{i=1}^k \lambda_i f_i (x)\right)\tag{24}$$
而
$$Z=\int \exp\left(-\sum_{i=1}^k \lambda_i f_i (x)\right)dx\tag{25}$$
同样需要将式$(24)$代入
$$\int p(x)f_i(x)dx -\tau_i=0,\quad (i=1,2,\dots,k)\tag{26}$$
解得各个参数$\lambda_i$。

连续型的例子 #

连续型的求解有时候会容易一些。比如假如只有一个约束，$f(x)=x$，即知道变量的平均值，那么概率分布为指数分布
$$p(x)=\frac{1}{Z}\exp\left(-\lambda x\right)\tag{27}$$
归一化因子为
$$\int_0^{\infty} \exp\left(-\lambda x\right) dx = \frac{1}{\lambda}\tag{28}$$
所以概率分布为
$$p(x)=\lambda \exp\left(-\lambda x\right)\tag{29}$$
还有一个约束为
$$\tau=\int_0^{\infty} \lambda \exp\left(-\lambda x\right) x dx =\frac{1}{\lambda}\tag{30}$$
所以结果为
$$p(x)=\frac{1}{\tau} \exp\left(-\frac{x}{\tau}\right)\tag{31}$$

还有，如果有两个约束，分别是$f_1 (x)=x,f_2(x)=x^2$，这相当于知道变量的平均值和方差，那么概率分布为正态分布（注意，正态分布又出现了）
$$p(x)=\frac{1}{Z}\exp\left(-\lambda_1 x-\lambda_2 x^2\right)\tag{32}$$
归一化因子为
$$\int_{-\infty}^{\infty} \exp\left(-\lambda_1 x-\lambda_2 x^2\right) dx = \sqrt{\frac{\pi}{\lambda_2}}\exp\left(\frac{\lambda_1^2}{4\lambda_2}\right)\tag{33}$$
所以概率分布为
$$p(x)=\sqrt{\frac{\lambda_2}{\pi}}\exp\left(-\frac{\lambda_1^2}{4\lambda_2}\right) \exp\left(-\lambda_1 x-\lambda_2 x^2\right)\tag{34}$$
两个约束为
$$\begin{aligned}&\tau_1=\int_{-\infty}^{\infty} \sqrt{\frac{\lambda_2}{\pi}}\exp\left(-\frac{\lambda_1^2}{4\lambda_2}\right) \exp\left(-\lambda_1 x-\lambda_2 x^2\right) x dx =-\frac{\lambda_1}{2\lambda_2}\\
&\tau_2=\int_{-\infty}^{\infty} \sqrt{\frac{\lambda_2}{\pi}}\exp\left(-\frac{\lambda_1^2}{4\lambda_2}\right) \exp\left(-\lambda_1 x-\lambda_2 x^2\right) x^2 dx =\frac{\lambda_1^2+2 \lambda_2}{4 \lambda_2^2}
\end{aligned}\tag{35}$$
将所解得的结果代入$(34)$式得到
$$p(x)=\sqrt{\frac{1}{2\pi(\tau_2-\tau_1^2)}}\exp\left(-\frac{(x-\tau_1)^2}{2(\tau_2-\tau_1^2)}\right)\tag{36}$$
注意$\tau_2-\tau_1^2$正好是方差，因此结果正好是均值为$\tau_1$、方差为$\tau_2-\tau_1^2$的正态分布！！这又成为了正态分布的一个来源！

转载到请包括本文地址：https://spaces.ac.cn/archives/3552

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。