科学空间|Scientific Spaces

这是笔者参加今年的泰迪杯C题的论文简化版。虽然最后只评上了一个安慰奖，但个人感觉里边有些思路对爬虫工作还是有些参加价值的。所以还是放出来供大家参考一下。

简介

一个爬虫可以分为两个步骤：1.把网页下载下来；2.从网页中把所需要的信息抽取出来。这两个步骤都存在相应的技术难点。对于第一个步骤，难度在于如何应对各大网站的反爬虫措施，如访问频率过高则封IP或者给出验证码等，这需要根据不同网站的不同反爬虫措施来设计，理论上不存在通用的可能性。对于第二个步骤，传统的做法是设计对应的正则表达式，随着网站设计上日益多样化，正则表达式的写法也相应变得困难。

显然，想要得到一个通用的爬虫方案，用传统的正则表达式的方案是相当困难的。但如果我们跳出正则表达式的思维局限，从全局的思维来看网站，结合DOM树来解析，那么可以得到一个相当通用的方案。因此，本文的主要内容，是围绕着爬虫的第二个步骤进行展开。本文的工作分为两个部分进行：首先，提出了一个适用于一般网站的信息抽取方案，接着，将这个方案细化，落实到论坛的信息抽取上。

点击阅读全文...

警告

以下内容包含诸多高危动作，请勿随意模仿。未成年人请在父母的陪同下观看～(^_^）

自杀式

Linux系统（下面内容同时适用于Mac OS）以开源自由闻名，然而有些时候它也开放过头了，而笔者也被它无比开发的特性坑了好几次（当然，主要是笔者使用习惯不好），遂总结分享，供大家娱乐。

最经典的例子就是，通过以下命令就可以实现“自杀”：

sudo rm / -rf

这就把你的Linux系统给毁了。显然，如果是在Windows中，这相当于在操作系统中格式化系统盘，这是绝对不允许的。

点击阅读全文...

baidu_jingsai

前两年百度的大数据竞赛都是自然语言处理方面的，今年画风一转，变成了图像的细颗粒度分类，赛题内容就是将宠物狗归为100类中的其中一类。这个任务本身是很平凡的，做法也很常规，无外乎就是数据扩增、imagenet模型的fine tune、模型集成三个方面。笔者并不擅长于模型集成，只做了前面两个步骤，成绩也非常一般（准确率80%上下）。但感觉里边的某些代码可能对读者有帮助，遂共享一翻。下面结合着代码来讲解。

比赛官网（随时有失效的可能）：http://js.baidu.com

模型

模型主要用tensorflow+keras实现。首先自然是导入各种模块

#! -*- coding:utf-8 -*-

import numpy as np
from scipy import misc
import tensorflow as tf
from keras.applications.xception import Xception,preprocess_input
from keras.layers import Input,Dense,Lambda,Embedding
from keras.layers.merge import multiply
from keras import backend as K
from keras.models import Model
from keras.optimizers import SGD
from tqdm import tqdm
import glob
np.random.seed(2017)
tf.set_random_seed(2017)

点击阅读全文...

最后，我们来看一下词向量模型$(15)$会有什么好的性质，或者说，如此煞费苦心去构造一个新的词向量模型，会得到什么回报呢？

模长的含义

似乎所有的词向量模型中，都很少会关心词向量的模长。有趣的是，我们上述词向量模型得到的词向量，其模长还能在一定程度上代表着词的重要程度。我们可以从两个角度理解这个事实。

在一个窗口内的上下文，中心词重复出现概率其实是不大的，是一个比较随机的事件，因此可以粗略地认为
\[P(w,w) \sim P(w)\tag{24}\]
所以根据我们的模型，就有
\[e^{\langle\boldsymbol{v}_{w},\boldsymbol{v}_{w}\rangle} =\frac{P(w,w)}{P(w)P(w)}\sim \frac{1}{P(w)}\tag{25}\]
所以
\[\Vert\boldsymbol{v}_{w}\Vert^2 \sim -\log P(w)\tag{26}\]
可见，词语越高频（越有可能就是停用词、虚词等），对应的词向量模长就越小，这就表明了这种词向量的模长确实可以代表词的重要性。事实上，$-\log P(w)$这个量类似IDF，有个专门的名称叫ICF，请参考论文《TF-ICF: A New Term Weighting Scheme for Clustering Dynamic Data Streams》。

点击阅读全文...

Geoffrey Hinton在谷歌多伦多办公室

由深度学习先驱Hinton开源的Capsule论文《Dynamic Routing Between Capsules》，无疑是去年深度学习界最热点的消息之一。得益于各种媒体的各种吹捧，Capsule被冠以了各种神秘的色彩，诸如“抛弃了梯度下降”、“推倒深度学习重来”等字眼层出不穷，但也有人觉得Capsule不外乎是一个新的炒作概念。

本文试图揭开让人迷惘的云雾，领悟Capsule背后的原理和魅力，品尝这一顿Capsule盛宴。同时，笔者补做了一个自己设计的实验，这个实验能比原论文的实验更有力说明Capsule的确产生效果了。

菜谱一览：

1、Capsule是什么？

2、Capsule为什么要这样做？

3、Capsule真的好吗？

4、我觉得Capsule怎样？

5、若干小菜。

点击阅读全文...

在本文中，我们再次对Capsule进行一次分析。

整体上来看，Capsule算法的细节不是很复杂，对照着它的流程把Capsule用框架实现它基本是没问题的。所以，困难的问题是理解Capsule究竟做了什么，以及为什么要这样做，尤其是Dynamic Routing那几步。

为什么我要反复对Capsule进行分析？这并非单纯的“炒冷饭”，而是为了得到对Capsule原理的理解。众所周知，Capsule给人的感觉就是“有太多人为约定的内容”，没有一种“虽然我不懂，但我相信应该就是这样”的直观感受。我希望尽可能将Capsule的来龙去脉思考清楚，使我们能觉得Capsule是一个自然、流畅的模型，甚至对它举一反三。

在《揭开迷雾，来一顿美味的Capsule盛宴》中，笔者先分析了动态路由的结果，然后指出输出是输入的某种聚类，这个“从结果到原因”的过程多多少少有些望文生义的猜测成分；这次则反过来，直接确认输出是输入的聚类，然后反推动态路由应该是怎样的，其中含糊的成分大大减少。两篇文章之间有一定的互补作用。

点击阅读全文...

事实上，在论文《Dynamic Routing Between Capsules》发布不久后，一篇新的Capsule论文《Matrix Capsules with EM Routing》就已经匿名公开了（在ICLR 2018的匿名评审中），而如今作者已经公开，他们是Geoffrey Hinton, Sara Sabour, Nicholas Frosst。不出大家意料，作者果然有Hinton。

大家都知道，像Hinton这些“鼻祖级”的人物，发表出来的结果一般都是比较“重磅”的。那么，这篇新论文有什么特色呢？

在笔者的思考过程中，文章《Understanding Matrix capsules with EM Routing 》给了我颇多启示，知乎上各位大神的相关讨论也加速了我的阅读，在此表示感谢。

论文摘要

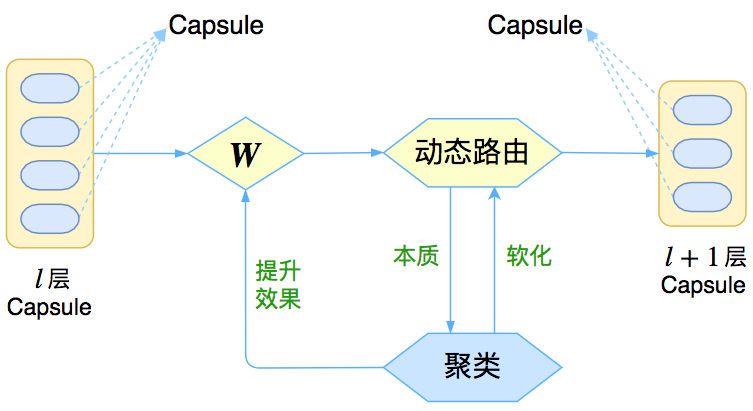
让我们先来回忆一下上一篇介绍《再来一顿贺岁宴：从K-Means到Capsule》中的那个图

Capsule框架的简明示意图

这个图表明，Capsule事实上描述了一个建模的框架，这个框架中的东西很多都是可以自定义的，最明显的是聚类算法，可以说“有多少种聚类算法就有多少种动态路由”。那么这次Hinton修改了什么呢？总的来说，这篇新论文有以下几点新东西：

1、原来用向量来表示一个Capsule，现在用矩阵来表示；

2、聚类算法换成了GMM（高斯混合模型）；

3、在实验部分，实现了Capsule版的卷积。

点击阅读全文...

最近在思考NLP的无监督学习和概率图相关的一些内容，于是重新把一些参数估计方法理了一遍。在深度学习中，参数估计是最基本的步骤之一了，也就是我们所说的模型训练过程。为了训练模型就得有个损失函数，而如果没有系统学习过概率论的读者，能想到的最自然的损失函数估计是平均平方误差，它也就是对应于我们所说的欧式距离。而理论上来讲，概率模型的最佳搭配应该是“交叉熵”函数，它来源于概率论中的最大似然函数。

最大似然

合理的存在

何为最大似然？哲学上有句话叫做“存在就是合理的”，最大似然的意思是“存在就是最合理的”。具体来说，如果事件$X$的概率分布为$p(X)$，如果一次观测中具体观测到的值分别为$X_1,X_2,\dots,X_n$，并假设它们是相互独立，那么
$$\mathcal{P} = \prod_{i=1}^n p(X_i)\tag{1}$$
是最大的。如果$p(X)$是一个带有参数$\theta$的概率分布式$p_{\theta}(X)$，那么我们应当想办法选择$\theta$，使得$\mathcal{L}$最大化，即
$$\theta = \mathop{\text{argmax}}_{\theta} \mathcal{P}(\theta) = \mathop{\text{argmax}}_{\theta}\prod_{i=1}^n p_{\theta}(X_i)\tag{2}$$

点击阅读全文...