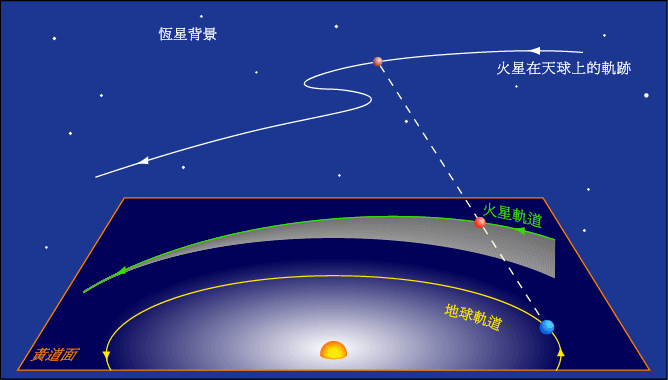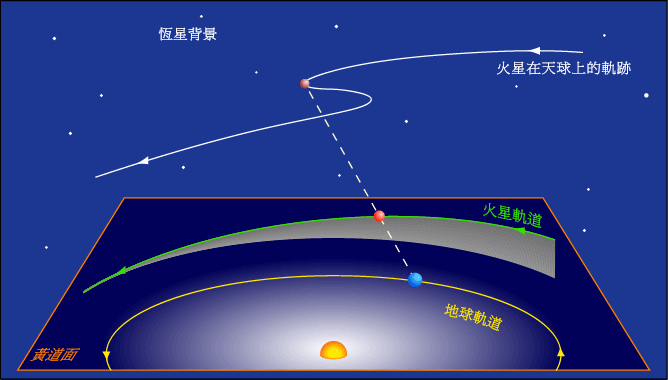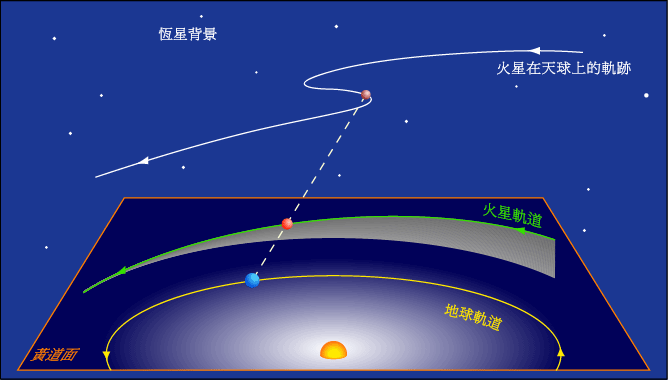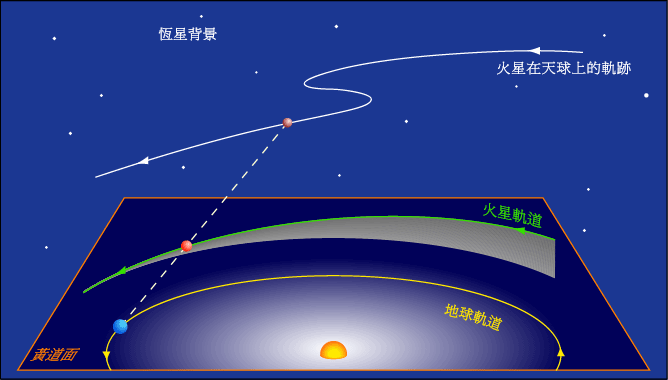
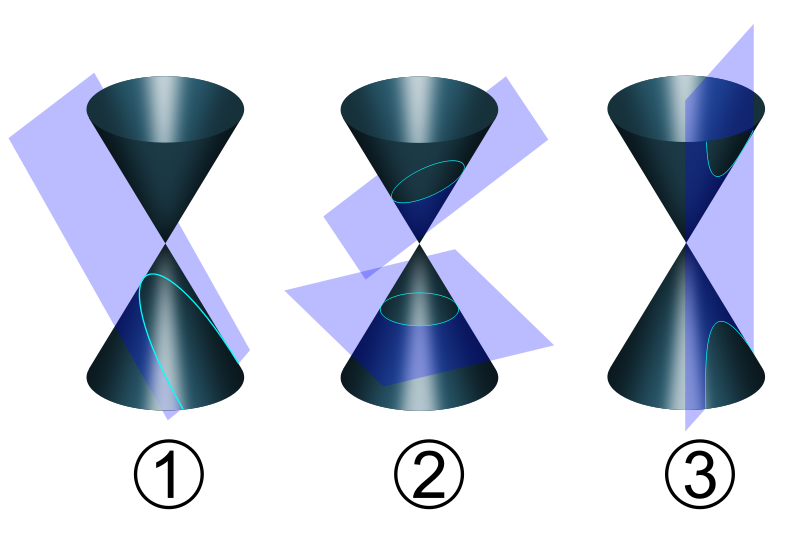
行星的逆行,顺行和留(计算公式)
By 苏剑林 | 2010-04-18 | 69785位读者 | 引用《方程与宇宙》:二体问题的来来去去(一)
By 苏剑林 | 2010-03-20 | 102906位读者 | 引用为了让大家能够查询到“天体力学”方面的内容,同时锻炼我的表达和计算能力,BoJone构思了《方程与宇宙》这个主题,主要是写一些关于使用数学相对深入地讨论一些天文问题。其实我一直觉得,不用公式是无法完美地描述科学的(当然也不能纯公式),我记得霍金的《时间简史》以及《果壳中的宇宙》等之类的书,都力求不用或者尽可能少用数学公式来表达自己的观点。这种模式对于对于公众来说是很好的,但是对于希望深入研究的朋友来说却难以进行。所以我主张:宇宙是算出来的!
这个主题每一个字都是由BoJone敲击出来的,其中包括引用了《天体力学引论》里面的一些内容,以及加入了BoJone个人的一些见解。由于篇幅长及时间有限问题,BoJone打算分若干次撰写发布,并且尽可能写得通俗一点,力求让有一点微积分基础的朋友就可以弄懂。这里首先发布第一部分。由于时间匆忙等原因,可能会出现一些疏忽,欢迎大家挑错!
谷歌搜索退出中国内地
By 苏剑林 | 2010-03-23 | 22139位读者 | 引用站长:Google终究还是退出了中国...当然,我们依旧能够使用它,尽管以后也许对中文的支持不会那么好。但是,值得思考的是,这是Google的RP问题,还是中国的政策问题?
北京时间3月23日凌晨3时零3分,谷歌公司高级副总裁、首席法律官大卫·德拉蒙德德(David Drummond)在一个博客中公开发表声明,宣布停止对谷歌中国搜索服务的“过滤审查”,并将搜索服务由中国内地转至香港。
他表示,登录google.cn的中国内地用户将被自动导向谷歌香港页面,使用服务器设在香港的未经审查的谷歌搜索(Google Search)、谷歌新闻(Google News)和谷歌图片(Google Images)服务。
声明还表示,谷歌公司并不会撤出中国内地,将保留在中国的销售和研发业务,保留未经审查的谷歌地图(Google Maps)等服务。谷歌600名中国雇员的去向仍未确定,他们有可能会被改派。
《方程与宇宙》:活力积分和开普勒方程(二)
By 苏剑林 | 2010-03-27 | 63244位读者 | 引用《方程与宇宙》:抛物线与双曲线轨道(三)
By 苏剑林 | 2010-04-03 | 55279位读者 | 引用关于自由落体公式的简单修正
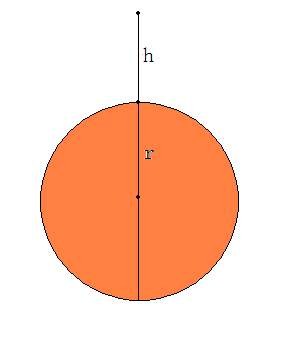
By 苏剑林 | 2010-04-04 | 73857位读者 | 引用自由落体的一般定义是:只考虑吸引天体和被吸引天体的引力因素,忽略其他的运动和大气摩擦等因素,物体从静止(相对于吸引天体)开始接近吸引天体的运动。根据这个定义,假设地球为一个均匀球体,半径为r,质量为M,物体从距离地表h高度处自由落下。求落到地面的时间t,或者根据时间t求h。
令s为t时刻物体左右下落的物体与地表的距离,忽略物体的小质量,那么可以列出微分方程:
d2sdt2=−GM(r+s)2并且初始条件是t=0,s=h,˙s=v=0
在实际应用中,我们不必求出这道微分方程的精确解,因为这个解极其麻烦,在之前曾经讨论过。我们只需要求出一个有足够精确度的近似解就行。










最近评论