有限内存下全局打乱几百G文件(Python)
By 苏剑林 | 2021-09-08 | 83834位读者 | 引用这篇文章我们来做一道编程题:
如何在有限内存下全局随机打乱(Shuffle)几百G的文本文件?
题目背景其实很明朗,现在预训练模型动辄就几十甚至几百G语料了,为了让模型能更好地进行预训练,对训练语料进行一次全局的随机打乱是很有必要的。但对于很多人来说,几百G的语料往往比内存还要大,所以如何能在有限内存下做到全局的随机打乱,便是一个很值得研究的问题了。
已有工具
假设我们的文件是按行存储的,也就是一行代表一个样本,我们要做的就是按行随机打乱文件。假设我们只有一个文件,并且这个文件大小明显小于内存,那么我们可以用linux自带的shuf命令:
shuf input.txt -o output.txt曾被嫌弃的预训练任务NSP,做出了优秀的Zero Shot效果
By 苏剑林 | 2021-09-10 | 61191位读者 | 引用在五花八门的预训练任务设计中,NSP通常认为是比较糟糕的一种,因为它难度较低,加入到预训练中并没有使下游任务微调时有明显受益,甚至RoBERTa的论文显示它会带来负面效果。所以,后续的预训练工作一般有两种选择:一是像RoBERTa一样干脆去掉NSP任务,二是像ALBERT一样想办法提高NSP的难度。也就是说,一直以来NSP都是比较“让人嫌弃”的。
不过,反转来了,NSP可能要“翻身”了。最近的一篇论文《NSP-BERT: A Prompt-based Zero-Shot Learner Through an Original Pre-training Task--Next Sentence Prediction》(下面简称NSP-BERT)显示NSP居然也可以做到非常不错的Zero Shot效果!这又是一个基于模版(Prompt)的Few/Zero Shot的经典案例,只不过这一次的主角是NSP。
背景回顾
曾经我们认为预训练纯粹就是预训练,它只是为下游任务的训练提供更好的初始化,像BERT的预训练任务有MLM(Masked Language Model和NSP(Next Sentence Prediction),在相当长的一段时间内,大家都不关心这两个预训练任务本身,而只是专注于如何通过微调来使得下游任务获得更好的性能。哪怕是T5将模型参数训练到了110亿,走的依然是“预训练+微调”这一路线。
GPLinker:基于GlobalPointer的事件联合抽取
By 苏剑林 | 2022-02-21 | 89175位读者 | 引用大约两年前,笔者在百度的“2020语言与智能技术竞赛”中首次接触到了事件抽取任务,并在文章《bert4keras在手,baseline我有:百度LIC2020》中分享了一个转化为BERT+CRF做NER的简单baseline。不过,当时的baseline更像是一个用来凑数的半成品,算不上一个完整的事件抽取模型。而这两年来,关系抽取的模型层见迭出,SOTA一个接一个,但事件抽取似乎没有多亮眼的设计。
最近笔者重新尝试了事件抽取任务,在之前的关系抽取模型GPLinker的基础上,结合完全子图搜索,设计一个比较简单但相对完备的事件联合抽取模型,依然称之为GPLinker,在此请大家点评一番。
任务简介
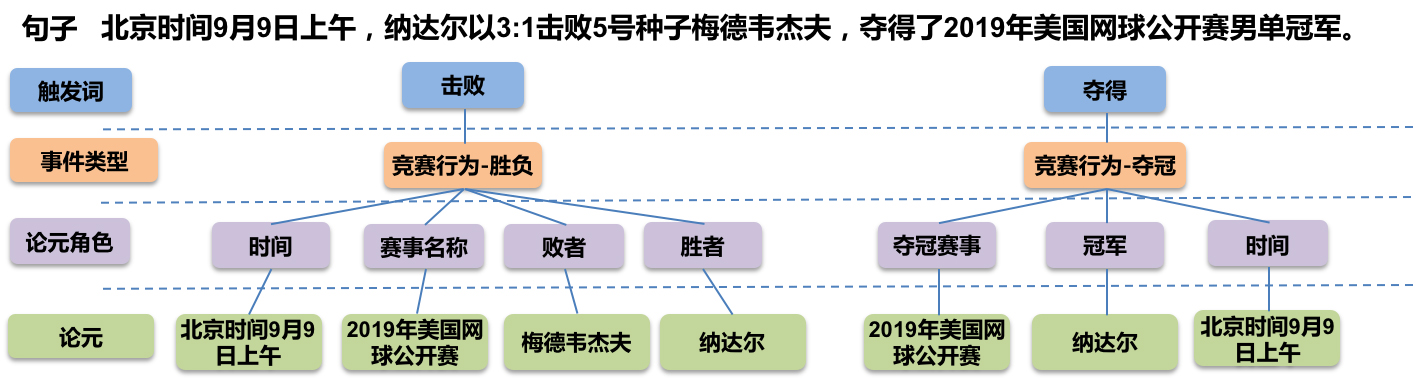
事件抽取是一个比较综合的任务。一个标准的事件抽取样本如下:
Ladder Side-Tuning:预训练模型的“过墙梯”
By 苏剑林 | 2022-06-20 | 83191位读者 | 引用如果说大型的预训练模型是自然语言处理的“张良计”,那么对应的“过墙梯”是什么呢?笔者认为是高效地微调这些大模型到特定任务上的各种技巧。除了直接微调全部参数外,还有像Adapter、P-Tuning等很多参数高效的微调技巧,它们能够通过只微调很少的参数来达到接近全量参数微调的效果。然而,这些技巧通常只是“参数高效”而并非“训练高效”,因为它们依旧需要在整个模型中反向传播来获得少部分可训练参数的梯度,说白了,就是可训练的参数确实是少了很多,但是训练速度并没有明显提升。
最近的一篇论文《LST: Ladder Side-Tuning for Parameter and Memory Efficient Transfer Learning》则提出了一个新的名为“Ladder Side-Tuning(LST)”的训练技巧,它号称同时达到了参数高效和训练高效。是否真有这么理想的“过墙梯”?本来就让我们一起来学习一下。
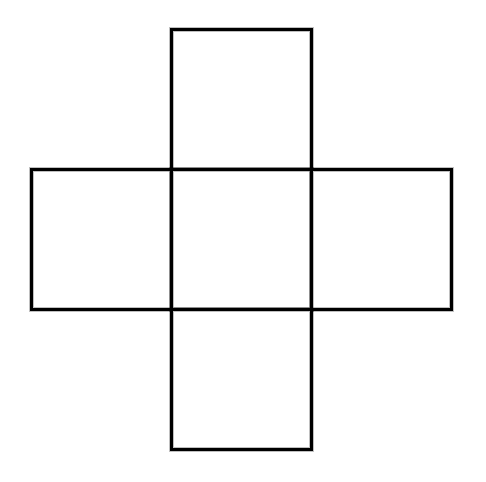
“十字架”组合计数问题浅试
By 苏剑林 | 2022-10-09 | 23989位读者 | 引用注意力和Softmax的两点有趣发现:鲁棒性和信息量
By 苏剑林 | 2023-04-25 | 37822位读者 | 引用【生活杂记】炒锅的尽头是铁锅
By 苏剑林 | 2023-11-13 | 66298位读者 | 引用很多会下厨的同学估计都纠结过一件事情,那就是炒锅的选择。
对于炒锅的纠结,归根结底是不粘与方便的权衡。最简单的不粘锅自然是带涂层的不粘锅,如果家里的热源只有电磁炉,并且炒菜习惯比较温和,那么涂层不粘锅往往是最佳选择了。不过,一旦有了明火的燃气灶,又或者是比较喜欢爆炒,那么涂层锅可能就不是那么适合了,毕竟温度过高涂层总有脱落的风险,此时一般就考虑无涂层不粘锅。
无涂层不粘锅也有五花八门的选择,比如朴素的铁锅、带蜂窝纹的不锈钢锅、有钛锅、纯钛锅等等,价格大体上也单调递增。不过用到最后,我觉得大部分人都会回归到朴素的铁锅。










最近评论