让MathJax更好地兼容谷歌翻译和延时加载
By 苏剑林 | 2024-08-15 | 30057位读者 | Kimi 引用很早之前,就有读者提出希望把Cool Papers上面的数学公式渲染一下,因为很多偏数学的论文,它们的摘要甚至标题上都带有LaTeX代码写的数学公式,如果不把这些公式渲染出来,那么看上去就像是一堆乱码,确实会比较影响阅读体验。然而,之前的测试显示,负责渲染公式的MathJax跟谷歌翻译和延时加载都不大兼容,所以尽管需求存在已久,但笔者一直没有把它加上去。
不过好消息是,经过反复查阅和调试,这两天笔者总算把兼容性问题解决了,所以现在大家看到的Cool Papers已经能够渲染数学公式了。这篇文章总结一下解决方案,供大家参考。
“Cool Papers + 站内搜索”的一些新尝试
By 苏剑林 | 2024-08-12 | 27398位读者 | Kimi 引用在《Cool Papers更新:简单搭建了一个站内检索系统》这篇文章中,我们介绍了Cool Papers新增的站内搜索系统。搜索系统的目的,自然希望能够帮助用户快速找到他们需要的论文。然而,如何高效地检索到对自己有价值的结果,并不是一件简单的事情,这里边往往需要一些技巧,比如精准提炼关键词。
这时候算法的价值就体现出来了,有些步骤人工来做会比较繁琐,但用算法来却很简单。所以接下来,我们将介绍几点通过算法来提高Cool Papers的搜索和筛选论文效率的新尝试。
相关论文
站内搜索背后的技术是全文检索引擎(Full-text Search Engine),简单来说,这就是一个基于关键词匹配的搜索算法,其相似度指标是BM25。
通向最优分布之路:概率空间的最小化
By 苏剑林 | 2024-08-06 | 35077位读者 | Kimi 引用当要求函数的最小值时,我们通常会先求导函数然后寻找其零点,比较幸运的情况下,这些零点之一正好是原函数的最小值点。如果是向量函数,则将导数改为梯度并求其零点。当梯度零点不易求得时,我们可以使用梯度下降来逐渐逼近最小值点。
以上这些都是无约束优化的基础结果,相信不少读者都有所了解。然而,本文的主题是概率空间中的优化,即目标函数的输入是一个概率分布,这类目标的优化更为复杂,因为它的搜索空间不再是无约束的,如果我们依旧去求解梯度零点或者执行梯度下降,所得结果未必能保证是一个概率分布。因此,我们需要寻找一种新的分析和计算方法,以确保优化结果能够符合概率分布的特性。
对此,笔者一直以来也感到颇为头疼,所以近来决定”痛定思痛“,针对概率分布的优化问题系统学习了一番,最后将学习所得整理在此,供大家参考。
对齐全量微调!这是我看过最精彩的LoRA改进(二)
By 苏剑林 | 2024-07-29 | 48256位读者 | Kimi 引用前两周笔者写了《对齐全量微调!这是我看过最精彩的LoRA(一)》(当时还没有编号“一”),里边介绍了一个名为“LoRA-GA”的LoRA变体,它通过梯度SVD来改进LoRA的初始化,从而实现LoRA与全量微调的对齐。当然,从理论上来讲,这样做也只能尽量对齐第一步更新后的$W_1$,所以当时就有读者提出了“后面的$W_2,W_3,\cdots$不管了吗?”的疑问,当时笔者也没想太深入,就单纯觉得对齐了第一步后,后面的优化也会严格一条较优的轨迹走。
有趣的是,LoRA-GA才出来没多久,arXiv上就新出了《LoRA-Pro: Are Low-Rank Adapters Properly Optimized?》,其所提的LoRA-Pro正好能回答这个问题!LoRA-Pro同样是想着对齐全量微调,但它对齐的是每一步梯度,从而对齐整条优化轨迹,这正好是跟LoRA-GA互补的改进点。
对齐全量
本文接着上一篇文章的记号和内容进行讲述,所以这里仅对上一节的内容做一个简单回顾,不再详细重复介绍。LoRA的参数化方式是
\begin{equation}W = (W_0 - A_0 B_0) + AB\end{equation}
Monarch矩阵:计算高效的稀疏型矩阵分解
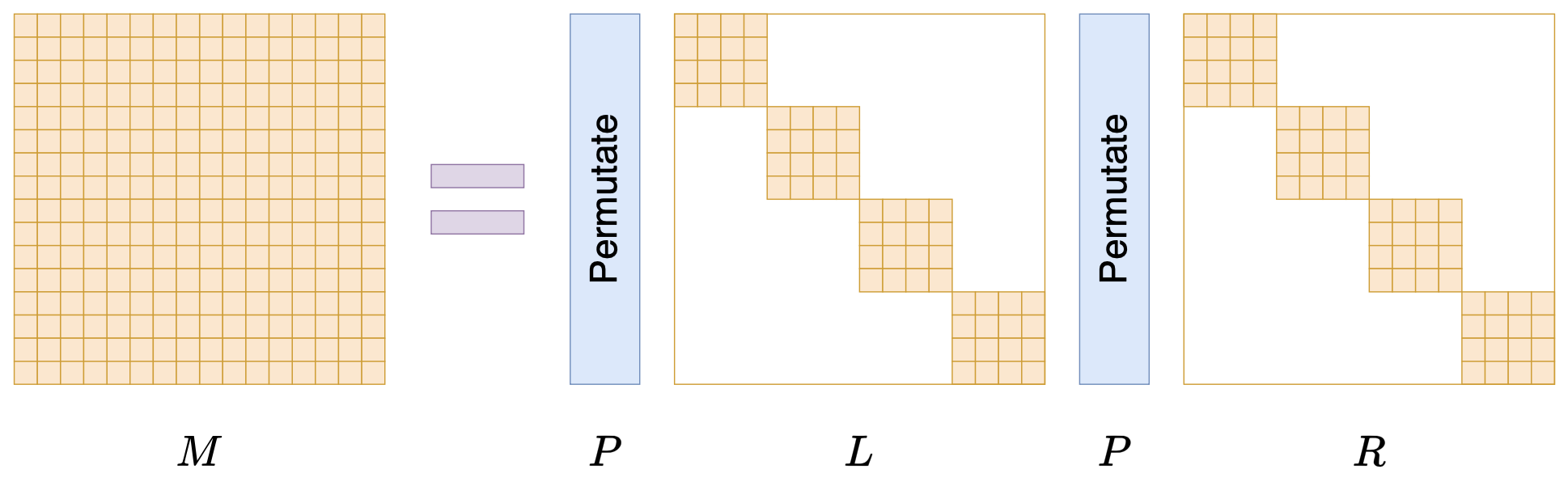
By 苏剑林 | 2024-07-24 | 51428位读者 | Kimi 引用在矩阵压缩这个问题上,我们通常有两个策略可以选择,分别是低秩化和稀疏化。低秩化通过寻找矩阵的低秩近似来减少矩阵尺寸,而稀疏化则是通过减少矩阵中的非零元素来降低矩阵的复杂性。如果说SVD是奔着矩阵的低秩近似去的,那么相应地寻找矩阵稀疏近似的算法又是什么呢?
接下来我们要学习的是论文《Monarch: Expressive Structured Matrices for Efficient and Accurate Training》,它为上述问题给出了一个答案——“Monarch矩阵”,这是一簇能够分解为若干置换矩阵与稀疏矩阵乘积的矩阵,同时具备计算高效且表达能力强的特点,论文还讨论了如何求一般矩阵的Monarch近似,以及利用Monarch矩阵参数化LLM来提高LLM速度等内容。
值得指出的是,该论文的作者也正是著名的Flash Attention的作者Tri Dao,其工作几乎都在致力于改进LLM的性能,这篇Monarch也是他主页上特意展示的几篇论文之一,单从这一点看就非常值得学习一番。
【生活杂记】用电饭锅来煮米汤
By 苏剑林 | 2024-07-17 | 24625位读者 | Kimi 引用对齐全量微调!这是我看过最精彩的LoRA改进(一)
By 苏剑林 | 2024-07-12 | 117631位读者 | Kimi 引用众所周知,LoRA是一种常见的参数高效的微调方法,我们在《梯度视角下的LoRA:简介、分析、猜测及推广》做过简单介绍。LoRA利用低秩分解来降低微调参数量,节省微调显存,同时训练好的权重可以合并到原始权重上,推理架构不需要作出改变,是一种训练和推理都比较友好的微调方案。此外,我们在《配置不同的学习率,LoRA还能再涨一点?》还讨论过LoRA的不对称性,指出给$A,B$设置不同的学习率能取得更好的效果,该结论被称为“LoRA+”。
为了进一步提升效果,研究人员还提出了不少其他LoRA变体,如AdaLoRA、rsLoRA、DoRA、PiSSA等,这些改动都有一定道理,但没有特别让人深刻的地方觉。然而,前两天的《LoRA-GA: Low-Rank Adaptation with Gradient Approximation》,却让笔者眼前一亮,仅扫了摘要就有种必然有效的感觉,仔细阅读后更觉得它是至今最精彩的LoRA改进。
究竟怎么个精彩法?LoRA-GA的实际含金量如何?我们一起来学习一下。
“闭门造车”之多模态思路浅谈(二):自回归
By 苏剑林 | 2024-07-08 | 153963位读者 | Kimi 引用这篇文章我们继续来闭门造车,分享一下笔者最近对多模态学习的一些新理解。
在前文《“闭门造车”之多模态思路浅谈(一):无损输入》中,我们强调了无损输入对于理想的多模型模态的重要性。如果这个观点成立,那么当前基于VQ-VAE、VQ-GAN等将图像离散化的主流思路就存在能力瓶颈,因为只需要简单计算一下信息熵就可以表明离散化必然会有严重的信息损失,所以更有前景或者说更长远的方案应该是输入连续型特征,比如直接将图像的原始像素特征Patchify后输入到模型中。
然而,连续型输入对于图像理解自然简单,但对图像生成来说则引入了额外的困难,因为非离散化无法直接套用文本的自回归框架,多少都要加入一些新内容如扩散,这就引出了本文的主题——如何进行多模态的自回归学习与生成。当然,非离散化只是表面的困难,更艰巨的部份还在后头...
无损含义
首先我们再来明确一下无损的含义。无损并不是指整个计算过程中一丁点损失都不能有,这不现实,也不符合我们所理解的深度学习的要义——在2015年的文章《闲聊:神经网络与深度学习》我们就提到过,深度学习成功的关键是信息损失。所以,这里无损的含义很简单,单纯是希望作为模型的输入来说尽可能无损。







 感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持!
感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持! 科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。
科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。 


最近评论