低秩近似之路(三):CR
By 苏剑林 | 2024-10-11 | 35776位读者 | Kimi 引用在《低秩近似之路(二):SVD》中,我们证明了SVD可以给出任意矩阵的最优低秩近似。那里的最优近似是无约束的,也就是说SVD给出的结果只管误差上的最小,不在乎矩阵的具体结构,而在很多应用场景中,出于可解释性或者非线性处理等需求,我们往往希望得到具有某些特殊结构的近似分解。
因此,从这篇文章开始,我们将探究一些具有特定结构的低秩近似,而本文将聚焦于其中的CR近似(Column-Row Approximation),它提供了加速矩阵乘法运算的一种简单方案。
问题背景
矩阵的最优$r$秩近似的一般提法是
\begin{equation}\mathop{\text{argmin}}_{\text{rank}(\tilde{\boldsymbol{M}})\leq r}\Vert \tilde{\boldsymbol{M}} - \boldsymbol{M}\Vert_F^2\label{eq:loss-m2}\end{equation}
低秩近似之路(二):SVD
By 苏剑林 | 2024-10-01 | 36716位读者 | Kimi 引用上一篇文章中我们介绍了“伪逆”,它关系到给定矩阵$\boldsymbol{M}$和$\boldsymbol{A}$(或$\boldsymbol{B}$)时优化目标$\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2$的最优解。这篇文章我们来关注$\boldsymbol{A},\boldsymbol{B}$都不给出时的最优解,即
\begin{equation}\mathop{\text{argmin}}_{\boldsymbol{A},\boldsymbol{B}}\Vert \boldsymbol{A}\boldsymbol{B} - \boldsymbol{M}\Vert_F^2\label{eq:loss-ab}\end{equation}
其中$\boldsymbol{A}\in\mathbb{R}^{n\times r}, \boldsymbol{B}\in\mathbb{R}^{r\times m}, \boldsymbol{M}\in\mathbb{R}^{n\times m},r < \min(n,m)$。说白了,这就是要寻找矩阵$\boldsymbol{M}$的“最优$r$秩近似(秩不超过$r$的最优近似)”。而要解决这个问题,就需要请出大名鼎鼎的“SVD(奇异值分解)”了。虽然本系列把伪逆作为开篇,但它的“名声”远不如SVD,听过甚至用过SVD但没听说过伪逆的应该大有人在,包括笔者也是先了解SVD后才看到伪逆。
接下来,我们将围绕着矩阵的最优低秩近似来展开介绍SVD。
结论初探
对于任意矩阵$\boldsymbol{M}\in\mathbb{R}^{n\times m}$,都可以找到如下形式的奇异值分解(SVD,Singular Value Decomposition):
\begin{equation}\boldsymbol{M} = \boldsymbol{U}\boldsymbol{\Sigma} \boldsymbol{V}^{\top}\end{equation}
利用“熄火保护 + 通断器”实现燃气灶智能关火
By 苏剑林 | 2024-09-26 | 32900位读者 | Kimi 引用Softmax后传:寻找Top-K的光滑近似
By 苏剑林 | 2024-09-19 | 69522位读者 | Kimi 引用Softmax,顾名思义是“soft的max”,是$\max$算子(准确来说是$\text{argmax}$)的光滑近似,它通过指数归一化将任意向量$\boldsymbol{x}\in\mathbb{R}^n$转化为分量非负且和为1的新向量,并允许我们通过温度参数来调节它与$\text{argmax}$(的one hot形式)的近似程度。除了指数归一化外,我们此前在《通向概率分布之路:盘点Softmax及其替代品》也介绍过其他一些能实现相同效果的方案。
我们知道,最大值通常又称Top-1,它的光滑近似方案看起来已经相当成熟,那读者有没有思考过,一般的Top-$k$的光滑近似又是怎么样的呢?下面让我们一起来探讨一下这个问题。
问题描述
设向量$\boldsymbol{x}=(x_1,x_2,\cdots,x_n)\in\mathbb{R}^n$,简单起见我们假设它们两两不相等,即$i\neq j \Leftrightarrow x_i\neq x_j$。记$\Omega_k(\boldsymbol{x})$为$\boldsymbol{x}$最大的$k$个分量的下标集合,即$|\Omega_k(\boldsymbol{x})|=k$以及$\forall i\in \Omega_k(\boldsymbol{x}), j \not\in \Omega_k(\boldsymbol{x})\Rightarrow x_i > x_j$。我们定义Top-$k$算子$\mathcal{T}_k$为$\mathbb{R}^n\mapsto\{0,1\}^n$的映射:
\begin{equation}
[\mathcal{T}_k(\boldsymbol{x})]_i = \left\{\begin{aligned}1,\,\, i\in \Omega_k(\boldsymbol{x}) \\ 0,\,\, i \not\in \Omega_k(\boldsymbol{x})\end{aligned}\right.
\end{equation}
说白了,如果$x_i$属于最大的$k$个元素之一,那么对应的位置变成1,否则变成0,最终结果是一个Multi-Hot向量,比如$\mathcal{T}_2([3,2,1,4]) = [1,0,0,1]$。
低秩近似之路(一):伪逆
By 苏剑林 | 2024-09-15 | 51877位读者 | Kimi 引用可能很多读者跟笔者一样,对矩阵的低秩近似有种熟悉而又陌生的感觉。熟悉是因为,低秩近似的概念和意义都不难理解,加之目前诸如LoRA等基于低秩近似的微调技术遍地开花,让低秩近似的概念在耳濡目染间就已经深入人心;然而,低秩近似所覆盖的内容非常广,在低秩近似相关的论文中时常能看到一些不熟悉但又让我们叹为观止的新技巧,这就导致了一种似懂非懂的陌生感。
因此,在这个系列文章中,笔者将试图系统梳理一下矩阵低秩近似相关的理论内容,以补全对低秩近似的了解。而在第一篇文章中,我们主要介绍低秩近似系列中相对简单的一个概念——伪逆。
优化视角
伪逆(Pseudo Inverse),也称“广义逆(Generalized Inverse)”,顾名思义就是“广义的逆矩阵”,它实际上是“逆矩阵”的概念对于不可逆矩阵的推广。
“闭门造车”之多模态思路浅谈(三):位置编码
By 苏剑林 | 2024-09-06 | 122699位读者 | Kimi 引用在前面的文章中,我们曾表达过这样的观点:多模态LLM相比纯文本LLM的主要差异在于,前者甚至还没有形成一个公认为标准的方法论。这里的方法论,不仅包括之前讨论的生成和训练策略,还包括一些基础架构的设计,比如本文要谈的“多模态位置编码”。
对于这个主题,我们之前在《Transformer升级之路:17、多模态位置编码的简单思考》就已经讨论过一遍,并且提出了一个方案(RoPE-Tie)。然而,当时笔者对这个问题的思考仅处于起步阶段,存在细节考虑不周全、认识不够到位等问题,所以站在现在的角度回看,当时所提的方案与完美答案还有明显的距离。
因此,本文我们将自上而下地再次梳理这个问题,并且给出一个自认为更加理想的结果。
多模位置
多模态模型居然连位置编码都没有形成共识,这一点可能会让很多读者意外,但事实上确实如此。对于文本LLM,目前主流的位置编码是RoPE(RoPE就不展开介绍了,假设读者已经熟知),更准确来说是RoPE-1D,因为原始设计只适用于1D序列。后来我们推导了RoPE-2D,这可以用于图像等2D序列,按照RoPE-2D的思路我们可以平行地推广到RoPE-3D,用于视频等3D序列。
Decoder-only的LLM为什么需要位置编码?
By 苏剑林 | 2024-09-01 | 88726位读者 | Kimi 引用众所周知,目前主流的LLM,都是基于Causal Attention的Decoder-only模型(对此我们在《为什么现在的LLM都是Decoder-only的架构?》也有过相关讨论),而对于Causal Attention,已经有不少工作表明它不需要额外的位置编码(简称NoPE)就可以取得非平凡的结果。然而,事实是主流的Decoder-only LLM都还是加上了额外的位置编码,比如RoPE、ALIBI等。
那么问题就来了:明明说了不加位置编码也可以,为什么主流的LLM反而都加上了呢?不是说“多一事不如少一事”吗?这篇文章我们从三个角度给出笔者的看法:
1、位置编码对于Attention的作用是什么?
2、NoPE的Causal Attention是怎么实现位置编码的?
3、NoPE实现的位置编码有什么不足?
近乎完美地解决MathJax与Marked的冲突
By 苏剑林 | 2024-08-26 | 22587位读者 | Kimi 引用在《让MathJax更好地兼容谷歌翻译和延时加载》我们提到Cool Papers加入了MathJax来解析LaTeX公式,不过万万没想到引发了诸多兼容性问题,虽然部分问题纯粹是笔者的强迫症作祟,但一个尽可能完美的解决方案终究是让人赏心悦目的,所以还是愿意在上面花一点心思。
上一篇文章我们已经解决了MathJax与谷歌翻译、延时加载的兼容性,这篇文章我们则来解决MathJax与Marked的冲突。
问题简述
Markdown是一种轻量级标记语言,允许人们使用易读易写的纯文本格式编写文档,可谓是目前最流行的写作语法之一,Cool Papers中的[Kimi]功能,基本上也是按照Markdown语法输出。然而。Markdown并不是直接面向浏览器的语言,面向浏览器的语言叫做HTML,所以在展示给用户之前,有一个Markdown转HTML的过程(渲染)。







 感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持!
感谢国家天文台LAMOST项目之“宇宙驿站”提供网络空间和数据库资源! 感谢国家天文台崔辰州博士等人的多方努力和技术支持! 科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。
科学空间致力于知识分享,所以欢迎您转载本站文章,但转载本站内容必须遵循 署名-非商业用途-保持一致 的创作共用协议。 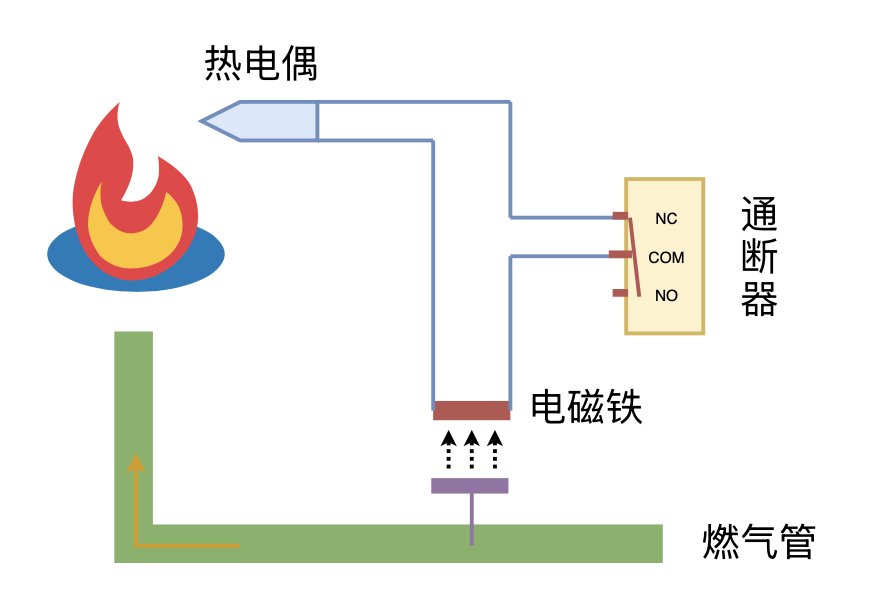

最近评论