外出集训,网站暂停更新...
By 苏剑林 | 2010-07-07 | 38635位读者 | 引用第114号化学元素再次被实验确认
By 苏剑林 | 2010-06-28 | 20503位读者 | 引用威力巨大的“有向线段”
By 苏剑林 | 2010-06-27 | 25421位读者 | 引用再次错过了“食”...
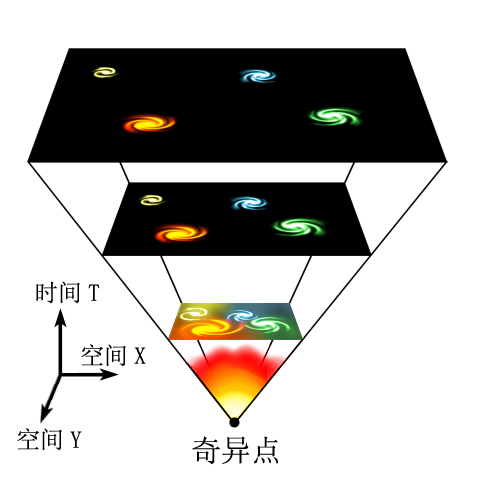
By 苏剑林 | 2010-06-26 | 38063位读者 | 引用从牛顿力学角度研究宇宙学
By 苏剑林 | 2010-06-17 | 70337位读者 | 引用不少天文爱好者对宇宙学这方面的内容“听而生畏”,觉得没有爱因斯坦的广义相对论等复杂理论基础是不可理解的。的确,这种观点没有错,当前的宇宙学对宇宙的精确描述,的确是建立在广义相对论和量子力学等理论的基础之上的。BoJone也只是在书上略略浏览,根本谈不上有什么了解。但是,对于一般的天文爱好者来说,只要对牛顿力学和微积分有一定的了解,就可以对我们的宇宙有一个大概的描述,也能够得出很多令人惊喜的结论。相信进行了这项工作之后,很多爱好者都会改观:原来宇宙学也并不是那么难...并且能够得出这样的一个结论:广义相对论虽然对牛顿引力理论进行了彻底的改革,但是从数学的角度来讲,它仅仅对牛顿力学进行了修正。
捉弄计划的失败——单摆周期
By 苏剑林 | 2010-06-09 | 54825位读者 | 引用“滴答滴答,滴答滴答——”当我们看到家里的摆钟来回摆动,并且能够准确地报时的时候,有没有想过其中的奥妙呢?
有一天,你想捉弄一下妈妈,把钟摆系上一个重物,心想着钟一定会走得更快,妈妈就会乱套了。可是很快你会失望地发现,摆钟依然准时地走着,没有任何异常,时间仿佛在宣告他的不可控制。你感到非常纳闷:为什么我的计划会失败呢?
据说,世界上第一个研究单摆的人是伽利略,他通过多次实验得出结论:单摆的周期只取决于摆绳的长度,和摆的重量无关。这是你明白了,原来要捉弄妈妈,应该要增加钟摆长度才对...^_^
现在我们来分析一下这个单摆....
高三高考用考场,我们就放假了。无奈高三正兴致勃勃地写着作文的同时,我们这群“低年级”也得写作文。这一次作文是标题作文——《人与路》
人与路的关系是什么?是人在走路,还是路在指引着人?
不同的人会有不同的答案。但是在我看来,智者总在走路,而愚者却在“被走路”。走路的人清楚自己的方向,敢于追逐自己所喜欢的,拥有无畏的精神;“被走路”的人无法找到心中的罗盘,就好比云雾中的星光,飘忽不定。两个人的路的终点都是一样的,只是一个人走到了,一个人没有走到。
当我们在人生的大海中航行时,我们是否能够认识到,我们究竟在“走路”还是“被走路”呢?只有自己走路,才能够更好地追逐自己的梦想,使自己的人生更上一层楼!













最近评论