Google新作试图“复活”RNN:RNN能否再次辉煌?
By 苏剑林 | 2023-03-28 | 90677位读者 |当前,像ChatGPT之类的LLM可谓是“风靡全球”。有读者留意到,几乎所有LLM都还是用最初的Multi-Head Scaled-Dot Attention,近年来大量的Efficient工作如线性Attention、FLASH等均未被采用。是它们版本效果太差,还是根本没有必要考虑效率?其实答案笔者在《线性Transformer应该不是你要等的那个模型》已经分析过了,只有序列长度明显超过hidden size时,标准Attention才呈现出二次复杂度,在此之前它还是接近线性的,它的速度比很多Efficient改进都快,而像GPT3用到了上万的hidden size,这意味着只要你的LLM不是面向数万长度的文本生成,那么用Efficient改进是没有必要的,很多时候速度没提上去,效果还降低了。
那么,真有数万甚至数十万长度的序列处理需求时,我们又该用什么模型呢?近日,Google的一篇论文《Resurrecting Recurrent Neural Networks for Long Sequences》重新优化了RNN模型,特别指出了RNN在处理超长序列场景下的优势。那么,RNN能否再次辉煌?
线性化 #
文章提出的RNN叫做LRU(Linear Recurrent Unit,线性循环单元),它是既可以并行又可以串行的极简线性RNN,训练和推断都具备高效的优势。LRU跟SSM(Structured State Model)、RWKV等工作有颇多相似之处。事实上,LRU的出发点就是发现SSM在LRA上表现很好,于是想办法将原生的RNN也能在LRA表现良好,其结果就是LRU。遗憾的是,原论文只在LRA(Long Range Arena,一个测试远程依赖能力的榜单)上做了实验,本文最后则会补充一些自己在语言模型上的实验结果。
原论文的介绍从SSM出发,并且花了不少篇幅描写LRU与SSM的关联。而在本文中,我们略过这些关联的描写,直接将LRU作为一个独立的RNN模型进行推演介绍。我们知道,最简单的RNN可以写为
\begin{equation}x_t = f(Ax_{t-1} + u_t)\end{equation}
其中$x_t,u_t\in\mathbb{R}^d,A\in\mathbb{R}^{d\times d}$,$f$是激活函数。一般情况下$u_t$之前、$x_t$之后都还有一个投影矩阵,但这里我们重点关注循环本身,因此就不把它显式写出来了。
传统的认知中,激活函数是非线性的,常见的选择有$\text{sigmoid},\tanh,\text{relu}$等,特别是有工作表明带有$\text{sigmoid}$或$\tanh$激活函数的单层RNN是图灵完备的,这就让人坚信非线性激活函数的必要性。然而,在深度学习中,实验才是检验真理的唯一标准,作者发现,如果将Transformer的Self Attention替换为RNN的话,线性RNN效果才是最好的:
这是一个让人意外的好消息。“意外”是因为可能会颠覆某些读者关于模型对非线性需求的认知;当然有些读者可能也不意外,因为MetaFormer等工作也表明过,得益于FFN层的强大,Self Attention等负责混合token的层的非线性可以很弱,甚至Pooling层都行。至于“好消息”,则是因为线性RNN有并行的实现算法,计算速度会大大快于非线性RNN。
于是,作者围绕线性RNN,进行了一系列探讨。
对角化 #
去掉激活函数,RNN就再次简化为
\begin{equation}x_t = Ax_{t-1} + u_t\label{eq:lr}\end{equation}
反复迭代得到
\begin{equation}x_0 = u_0\\ x_1 = Au_0 + u_1\\ x_2 = A^2 u_0 + Au_1 + u_2\\ \vdots \\ x_t = \sum_{k=0}^t A^{t-k}u_k\label{eq:lr-e}\end{equation}
可以看到,主要的计算量集中在矩阵$A$的幂运算上。这时候不难联想到矩阵对角化,它是计算矩阵幂的高效方法,然而一般的矩阵在实数域不一定能对角化。这时候我们该怎么办?格局打开点,既然实数域做不了,我们到复数域去!几乎所有矩阵都可以在复数域对角化,这意味着$A$总能写成
\begin{equation}A = P\Lambda P^{-1}\quad\Rightarrow\quad A^n = P\Lambda^n P^{-1}\end{equation}
其中$P,\Lambda\in\mathbb{C}^{d\times d}$,$\Lambda$是特征值组成的对角阵。代入式$\eqref{eq:lr-e}$我们得到:
\begin{equation}x_t = \sum_{k=0}^t P\Lambda^{t-k}P^{-1}u_k = P\left(\sum_{k=0}^t \Lambda^{t-k}(P^{-1}u_k)\right)\end{equation}
刚才我们说了,一般情况下$u_t$之前、$x_t$之后都还有一个投影矩阵,只要我们约定这两个投影矩阵都是复数矩阵,那么理论上$P$、$P^{-1}$都可以合并到它们的投影运算中,这就意味着,如果一切运算都在复数域中考虑,那么将线性RNN中的一般矩阵$A$换成对角阵$\Lambda$,模型能力不会有任何损失!所以我们只需考虑如下的极简RNN
\begin{equation}x_t = \Lambda x_{t-1} + u_t\quad\Rightarrow\quad x_t = \sum_{k=0}^t \Lambda^{t-k}u_k\label{eq:lr-x}\end{equation}
参数化 #
对角矩阵的好处是一切运算都是element-wise的,所以每个维度的运算可以充分并行,同时也意味着只要分析一个维度就相当于分析了所有维度,模型的分析只需要在一维空间进行。不妨设$\Lambda=\text{diag}(\lambda_1,\lambda_2,\cdots,\lambda_d)$,$\lambda$代表$\lambda_1,\lambda_2,\cdots,\lambda_d$中的一个,同时在不至于混淆的情况下,$x_t$、$u_t$同样也用来表示$\lambda$在它们之中对应的分量,于是$\eqref{eq:lr-x}$简化为标量运算:
\begin{equation}x_t = \lambda x_{t-1} + u_t\quad\Rightarrow\quad x_t = \sum_{k=0}^t \lambda^{t-k}u_k\label{eq:lr-xx}\end{equation}
注意别忘了,$\lambda$是复数,所以我们可以设$\lambda = re^{i\theta}$,其中$r \geq 0, \theta\in[0, 2\pi)$都是实数:
\begin{equation}x_t = \sum_{k=0}^t r^{t-k}e^{i(t-k)\theta}u_k\label{eq:lr-e-r-theta}\end{equation}
求和过程中$t-k$都是非负数,因此$r \leq 1$,要不然历史项的权重将会逐渐趋于无穷大,这跟直觉不符(直觉上对历史信息的依赖应该是逐步减弱的),也会梯度爆炸的风险;另一方面,如果$r \ll 1$,那么就会有梯度消失的风险。这就对$r$提出了两个要求:1、保证$r\in[0,1]$;2、初始化阶段$r$应该尽量接近1。
为此,我们先设$r = e^{-\nu}$,那么$r\in[0,1]$就要求$\nu\geq 0$,于是我们再设$\nu=e^{\nu^{\log}}$,这时候就有$\nu^{\log}\in\mathbb{R}$而转化为无约束优化了。这里的$\nu^{\log}$是另一个变量的记号,并非代表什么特殊的运算。而既然$\nu$被参数化为了$e^{\nu^{\log}}$,那么为了保持一致性,我们也将$\theta$参数化为$e^{\theta^{\log}}$。
可能读者要问,约束$r\in[0,1]$的方法有很多呀,为什么要搞这么复杂?直接加sigmoid不好吗?首先,将$r$参数化为$e^{-\nu}$后,幂运算可以跟$\theta$的结合在一起,即$r^k e^{ik\theta}=e^{k(-\nu+i\theta)}$,这样不管从实现角度还是计算角度都比较好;接着,因为$\nu\geq 0$,能将任何实数能映射为非负数的最简单的光滑函数,可能就是指数函数的,于是容易想到$\nu=e^{\nu^{\log}}$。SSM中采用的$\text{relu}$激活,即直接$r=e^{-\max(\nu,0)}$,但这会有个饱和区,可能不利于优化。
初始化 #
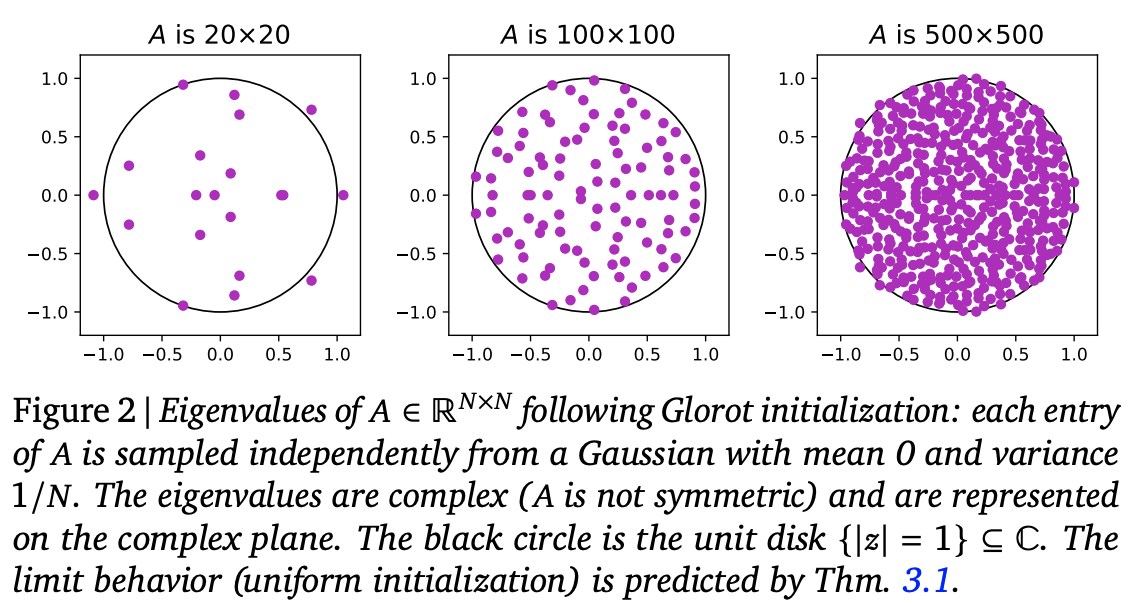
接下来考虑初始化问题。我们回到原始形式$\eqref{eq:lr}$,一个$d\times d$的实矩阵,标准的Glorot初始化是均值为0、方差为$1/d$的正态分布或者均匀分布(参考《从几何视角来理解模型参数的初始化策略》)。可以从理论或者实验上表明,这样的初始化矩阵,其特征值大致上均匀分布在复平面上的单位圆内:
由此,我们可以想到$\Lambda$的标准初始化方式是在复平面上的单位圆内均匀取点。而从笛卡尔坐标换到极坐标,我们有$dxdy=rdrd\theta=\frac{1}{2}d(r^2)d\theta$,这就告诉我们,要实现单位圆内均匀取点,只需要$\theta\sim U[0,2\pi]$以及$r^2\sim U[0,1]$。
然而,刚才我们说为了尽可能地预防梯度消失,我们至少要在初始化阶段让$r$尽量接近于1,所以改进方式是改在$r\in[r_{\min},r_{\max}]$的圆环内均匀采样,这样采样方式就变为$\theta\sim U[0,2\pi]$以及$r^2\sim U[r_{\min}^2,r_{\max}^2]$。原论文的实验结果显示,$r_{\min}=0.9,r_{\max}=0.999$对多数实验都有较好效果。
这里有一个问题,就是$r$初始化接近1,而初始阶段$u_t$也比较接近独立同分布的,那么式$\eqref{eq:lr-e-r-theta}$就接近若干个模长不变的求和(而不是平均),这就可能有爆炸风险。为了分析这一点,我们先写出
\begin{equation}|x_t|^2 = x_t x_t^* = \sum_{k=0}^t\sum_{l=0}^t r^{(t-k)+(t-l)}e^{i[(t-k)-(t-l)]\theta}u_k u_l^*\end{equation}
这里的$*$是复数的共轭运算,$|\cdot|$是复数的模。接着两端求期望,这里我们假设$u_k,u_l$独立地服从同一均值为0的分布,那么当$k\neq l$时,$\mathbb{E}[u_k u_l^*]=\mathbb{E}[u_k]\mathbb{E}[u_l^*]=0$,于是只剩下$k=l$的项非零,于是:
\begin{equation}\mathbb{E}[|x_t|^2] = \sum_{k=0}^t r^{2(t-k)}\mathbb{E}[u_k u_k^*] = \mathbb{E}[|u_k|^2]\sum_{k=0}^t r^{2(t-k)} = \frac{(1 - r^{2(t+1)})\mathbb{E}[|u_k|^2]}{1-r^2}\end{equation}
由于$r \in (0, 1)$,当$t$足够大时$r^{2(t+1)}\to 0$。这也就是说,当$t$比较大时,平均意义下$x_t$的模长与$u_k$的模长之比为$\frac{1}{\sqrt{1-r^2}}$,当$r$很接近1时,这个比例很大,也就是序列经过RNN后会膨胀得比较大,这不利于训练的稳定性。于是作者想了个简单的技巧,多引入一个element-wise的参数$\gamma$,初始化为$\sqrt{1-r^2}$,然后将式$\eqref{eq:lr-xx}$改为:
\begin{equation}x_t = \lambda x_{t-1} + \gamma u_t\quad\Rightarrow\quad x_t = \gamma\sum_{k=0}^t \lambda^{t-k} u_k\label{eq:lr-xxx}\end{equation}
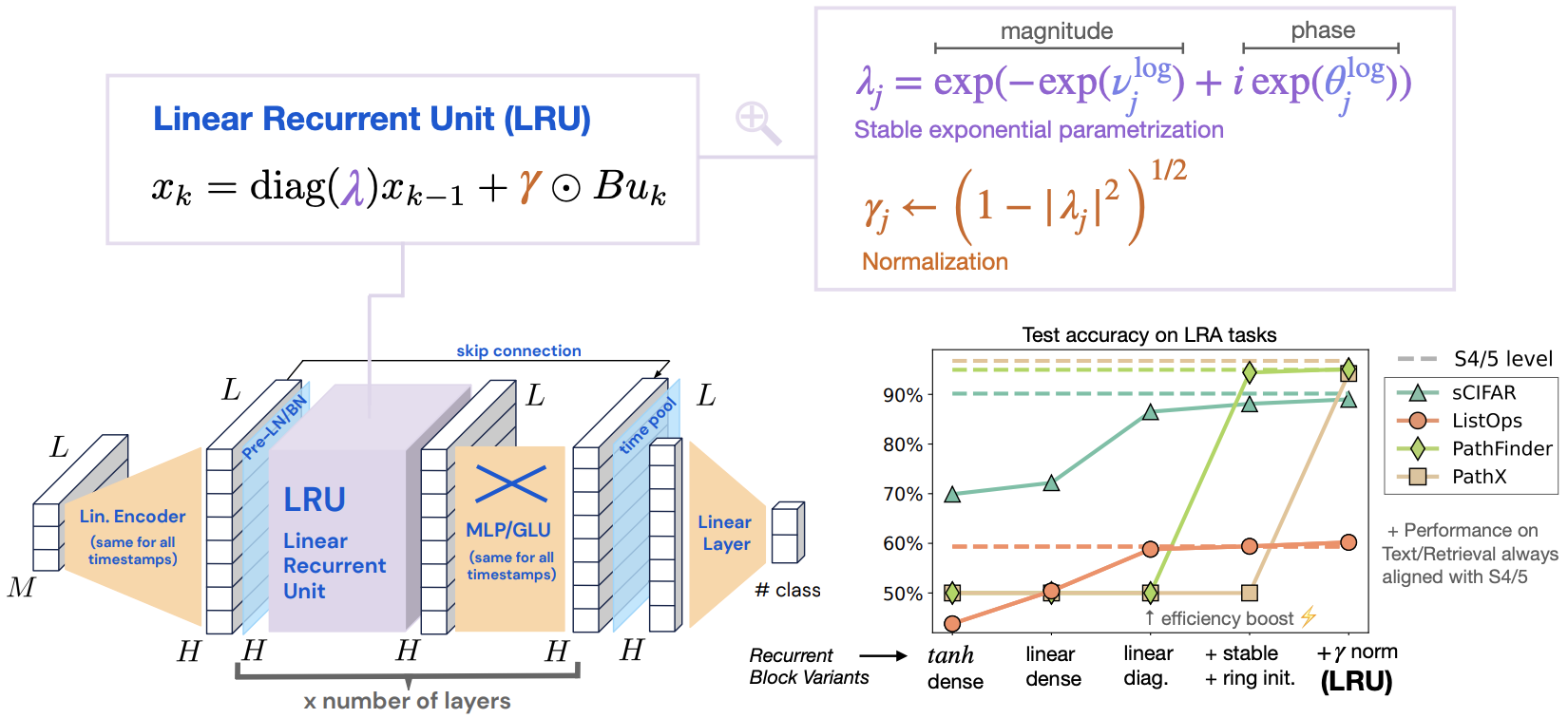
这样一来,至少在初始阶段模型的输出就稳定了,剩下就让模型自己学就好了。综合以上结果,就是原论文所提的LRU(Linear Recurrent Unit)模型了,如下图:
相关化 #
这里介绍LRU的两个相关变体。
SLRU #
LRU的出发点是对一般的线性RNN模型$\eqref{eq:lr}$进行简化,而为了在理论上达到一般矩阵的效果,就不得不引入复的投影矩阵,以及复的特征值对角阵$\Lambda$。如果我们不考虑达到一般矩阵的效果,纯粹关心$r$所带来的衰减作用,那么我们可以进一步简化LRU模型——假设投影矩阵和特征值对角阵都是实数——这个简化版我们称为SLRU(Simpler Linear Recurrent Unit)。
原论文并没有研究SLRU,但笔者感觉它更符合我们的直觉(主要是相位$\theta$的变化不容易从直觉上理解),所以在后面也补充了SLRU的实验。
RWKV #
谈到RNN,可能有读者听说过最近小有名气的RWKV,它可以看作SLRU/Hydra Attention和GLU(Gated Linear Unit)的结合。RWKV的RNN部分为:
\begin{equation}x_t = \sigma(r_t) \times\frac{y_t + (\gamma \lambda - 1)e^{k_t}v_t}{z_t + (\gamma \lambda - 1)e^{k_t}},\quad\begin{aligned}y_t =&\, \lambda y_{t-1} + e^{k_t}v_t \\ z_t =&\, \lambda z_{t-1} + e^{k_t}\end{aligned}\end{equation}
可以看到,递归部分就是两个SLRU,RWKV的特点是两个SLRU的结果相除,起到归一化的效果,所以就不需要LRU中的gamma技巧了。另外也许是为了跟Self Attention对齐参数量,或者是为了进一步提升效果,在归一化之后RWKV再添加了一个门$\sigma(r_t)$与之相乘。虽然作者在LM任务上已经验证过了RWKV的有效性,但它与常见模型的对照实验似乎没有出现过,本文也将补充这部分。
注:这里的RWKV特指负责token混合的RNN模块,并非指作者给出的完整模型(即没有用作者的Channel-Mix层、Time Shift等内容)。
代码化 #
这一节我们来讨论LRU的实现问题。原论文附录中给出了Jax版本的LRU参考代码,这里笔者也给出Keras版本的:
实现LRU有两个技术难点:复数化和并行化。
复数化 #
LRU的投影矩阵和特征值都是复的,作者给出的Jax版代码是直接使用复数矩阵的,换到Keras这意味着我们无法用回已有的Dense层,这未免有些遗憾。事实上,根据$(B+iC)u=Bu + iCu$我们可以看出,复数投影矩阵只不过是将投影维度增加一倍而已,所以投影部分我们就不用复数矩阵了,直接用两倍units的Dense层就行。
接着是$e^{i(t-k)}u_k$部分,这既可以直接展开为纯实数运算,也可以直接按照公式用复数运算。如果展开为实数运算的话,其形式跟RoPE是一样的,所以笔者刚开始看到LRU时就很激动,以为这不就是“RoPE is all you need”哈。不过笔者对比过速度,发现直接按照公式实现的复数版速度会稍快一些,所以建议还是用复数版的。
最后,就是复数输出投影回实矩阵问题,根据$\Re[(B+iC)(x+iy)]=Bx-Cy=[B,-C][x,y]^{\top}$,这意味着我们只需要将实部和虚部拼接起来,然后接一个Dense层就能实现了。
并行化 #
如果直接按照递归公式实现串行版的RNN,那么训练速度将会非常慢(预测都是串行的自回归,所以预测没问题)。前面说了,线性RNN的一个重要特性是它本身有并行算法,可以大大加快训练速度。
事实上,我们可以将$\eqref{eq:lr-xx}$改写为
\begin{equation}x_t = \lambda^t \sum_{k=0}^t \lambda^{-k} u_k\end{equation}
这其实已经告诉了我们一种快速的算法:每个$u_k$都乘以$\lambda^{-k}$,这是element-wise的,可以并行;然后$\sum\limits_{k=0}^t$这一步实际上就是cumsum运算,各个框架自带的实现都很快;最后就是cumsum的结果都乘以各自的$\lambda^t$,这一步也是element-wise的,可以并行。然而,因为$|\lambda| < 1$,所以当$k$很大时$\lambda^{-k}$几乎必定会爆炸,别说fp16精度了,在长序列时FP32甚至FP64都不一定能兜住。因此,这个看上去很简明的方案,理论上没有问题,实际上却没什么价值。
并行加速的关键,是留意到分解($T > t$)
\begin{equation}\begin{aligned}
x_T =&\, \sum_{k=0}^T \lambda^{T-k} u_k \\
=&\, \sum_{k=0}^t \lambda^{T-k} u_k + \sum_{k=t+1}^T \lambda^{T-k} u_k \\
=&\, \lambda^{T-t}\sum_{k=0}^t \lambda^{t-k} u_k + \sum_{k=t+1}^T \lambda^{T-k} u_k \\
\end{aligned}\end{equation}
这个分解告诉我们,对整个序列做$\eqref{eq:lr-xx}$的结果,等价于将序列分为两半各自做$\eqref{eq:lr-xx}$,然后将前一半的最后一个结果加权到后一半各个位置上,如下图左:
这里的关键是“分开两半各自做$\eqref{eq:lr-xx}$”这两半是可以并行的!于是递归下去,我们就将原本是$\mathcal{O}(L)$的循环步数改为了$\mathcal{O}(\log L)$,从而大大加快训练速度,如上图右。
事实上,这就是Prefix Sum问题的“Upper/Lower”并行算法,代码细节可以参考笔者上面给出的代码。因为Tensorflow 1.x不支持直接写递归,笔者是用tf.while_loop或者for从下到上实现的,训练时只能勉强接近Self Attention的速度。事实上如果将循环部分重写为CUDA内核的话,应该是可以超过Self Attention速度的(可惜笔者不会)。RWKV的作者只是将RWKV的RNN格式写成了CUDA内核,没有考虑并行化,但就这已经可以媲美Self Attention的速度了。
此外,Prefix Sum还有“Odd/Even”并行算法,理论上它的计算效率更高一些,但它的结构更复杂些,如果用tensorflow实现的话,它涉及到更多的循环步数以及更多的reshape和concat操作,实际效率未必比得上“Upper/Lower”并行算法,因此笔者就没有实现它了(主要还是tensorflow 1.x不支持递归导致的,如果用递归写倒不是太复杂)。
效果化 #
这一节我们将演示原论文在LRA上的实验结果,以及笔者在语言模型(LM)任务上的实验结果。
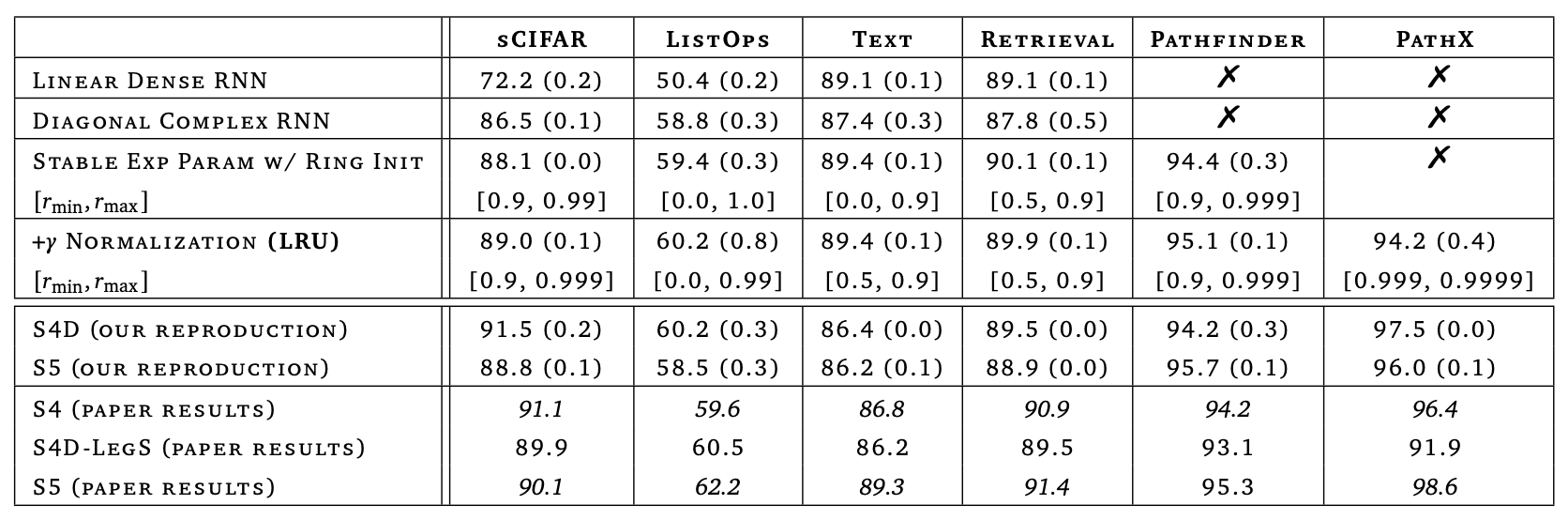
原论文中,作者主要是通过理论和实验相结合的方式,演示了如何一步步地优化普通的RNN,直到在LRA上取得接近SOTA的效果,这个分析和改进的过程可谓是引人入胜,值得反复品味。但由于原论文的实验都是在LRA上反复进行的,所以实验本身并无过多精彩之处,这里只演示论文中的Table 8:
对于本文的读者来说,可能更关心它在NLP尤其是近来很火的LM上的效果,可惜原论文没有这部分内容,笔者自己做了一些对比实验,供大家参考。对比的模型包括GAU(同GAU-α)、SA(同RoFormerV2)、LRU、SLRU和RWKV,其中LRU、SLRU、RWKV都只是将RoFormerV2中的Self Attention换成参数量和计算量相似的LRU、SLRU、RWKV。模型参数量均为1亿左右的base版,在当前算是小模型了,初始化均使用DeepNorm,优化器用的是Tiger,其他所有超参数都一致,基本上做到了比较严格的控制变量。
可以看到,从效果上排序,应该是
$$\text{GAU} > \text{SA} > \text{RWKV} > \text{LRU} > \text{SLRU}$$
从实验结果上我们可以得出:
1、LRU优于SLRU,表明引入复投影矩阵和复特征值确实是有帮助的,但计算效率会有一定损失(哪怕保持参数量不变);
2、当序列长度增加时,Attention系列(GAU、SA)的效果会变好,而RNN系列(LRU、SLRU、RWKV)的效果则会下降,这是两者的本质差异,原因应该是RNN的长程记忆能力受限于hidden_size;
3、RWKV确实有可能是目前最好的RNN模型,但跟Attention类(GAU、SA)模型还有明显的差距;
4、根据第2点,RNN系列需要追平Attention系列,那么应该需要继续放大hidden_size,所以在LM任务上RNN系列或许需要更大尺度才有优势;
5、结合第1点和第3点,下一个改进版的RNN是否就是复数版RWKV了?
此外,还有几点实验过程中的经验。由于GAU是单头的,因此在长序列、大尺度的场景下它的计算效率明显优于SA,并且它的效果也优于SA,所以GAU应该是在相当大的一个范围内是语言模型的最佳选择,拍脑袋想的话,百亿参数以内、序列长度5000以内,都建议优先考虑GAU。但不可否认,同尺度的RNN系列模型在推理效率上更优(每步递归的计算量和cache大小都一致),而训练效率上也不输于Attention系列,因此模型放大之后,应该还是有机会跟Attention系列一较高低的。
值得指出的是,RWKV虽然整体表现不错,但与GAU和SA的差距还是有的,所以公平比较之下,RWKV也没有传说中那么完美无暇。事实上,RWKV作者自己的实现中,就包含了一系列据说有助于增强LM效果但相当晦涩的trick(按照作者的意思,他这些trick才是“精华”),这些trick需要读作者给的源代码才能发现,它们没有考虑进笔者的实验中。不排除这些trick有助于更好训练一个LM的可能性,但笔者更多的是想做一个公平的对照实验而非实际训练一个LM模型,一旦引入这些trick,变量就太多了,笔者算力有限,无法一一对照。
当然,以上结论都只是在1亿级别的“小模型”中得出的,更大尺度的模型笔者还在尝试中,暂时没法给大家结论。
结论化 #
本文介绍了Google“拯救”RNN的一次尝试,自上而下地构建了一个在LRA上表现接近SOTA的高效RNN模型。除了原论文在LRA上的实验外,本文还给出了笔者自己在语言模型上的实验结果,包括与RWKV等相关模型的对比。总的来说,经过优化的RNN模型在训练效率上并不逊色于Attention类模型,同时有着更好的推理性能,但语言模型效果上离Attention类模型还有一定差距,也许需要将模型做得更大,才能进一步体现出RNN的优势。
转载到请包括本文地址:https://spaces.ac.cn/archives/9554
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Mar. 28, 2023). 《Google新作试图“复活”RNN:RNN能否再次辉煌? 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/9554
@online{kexuefm-9554,
title={Google新作试图“复活”RNN:RNN能否再次辉煌?},
author={苏剑林},
year={2023},
month={Mar},
url={\url{https://spaces.ac.cn/archives/9554}},
}












September 26th, 2023
[...]近年来,线性RNN由于其可并行训练以及常数推理成本等特性,吸引了一定研究人员的关注(例如笔者之前写的《Google新作试图“复活”RNN:RNN能否再次辉煌?》),这让RNN在Transformer遍地开花的潮流中仍有“一席之地”。然而,目前看来这“一席之地”只属于线性RNN,因为非线性RNN无法高效地并行训练,所以在架构之争中是“心有余而力不足”。[...]
October 4th, 2023
关于矩阵对角化的描述有误,绝大部分矩阵都是无法对角化的,也就是jordan标准型不是对角化的矩阵都无法对角化,比如矩阵[1, 1; 0, 1]就无法对角化
又思考了一下,从概率角度来看,出现相同特征值的概率为0,作者结论没问题,但是表述还是有问题,jordan标准型就是矩阵的最简表示,只是非对角的jordan矩阵出现的概率为0
再具体一点,jordan标准型本身就是在复数域才存在的分解方式,所以只是说作者的表述有些让人迷惑
没错误,在复数域中几乎所有方阵都可以对角化:https://en.wikipedia.org/wiki/Diagonalizable_matrix#Characterization
October 8th, 2023
是的, 结论是没错,只不过原文 "这时候我们该怎么办?考虑若当标准型?不,格局打开点,既然实数域做不了,我们到复数域去!" 表述存在问题, jordan标准型本身就是在复数域上成立的分解。
逻辑应该是 一个矩阵的jordan标准型是非对角矩阵 等价于 此矩阵的特征多项式存在重根,这在高维空间中出现的概率为0
原来如此,是我对若当标准型误解了,感谢指出,已更正。