多任务学习漫谈（二）：行梯度之事

在《多任务学习漫谈（一）：以损失之名》中，我们从损失函数的角度初步探讨了多任务学习问题，最终发现如果想要结果同时具有缩放不变性和平移不变性，那么用梯度的模长倒数作为任务的权重是一个比较简单的选择。我们继而分析了，该设计等价于将每个任务的梯度单独进行归一化后再相加，这意味着多任务的“战场”从损失函数转移到了梯度之上：看似在设计损失函数，实则在设计更好的梯度，所谓“以损失之名，行梯度之事”。

那么，更好的梯度有什么标准呢？如何设计出更好的梯度呢？本文我们就从梯度的视角来理解多任务学习，试图直接从设计梯度的思路出发构建多任务学习算法。

整体思路 #

我们知道，对于单任务学习，常用的优化方法就是梯度下降，那么它是怎么推导的呢？同样的思路能不能直接用于多任务学习呢？这便是这一节要回答的问题。

下降方向 #

其实第一个问题，我们在《从动力学角度看优化算法（三）：一个更整体的视角》就回答过。假设损失函数为$\mathcal{L}$，当前参数为$\boldsymbol{\theta}$，我们希望设计一个参数增量$\Delta\boldsymbol{\theta}$，它使得损失函数更小，即$\mathcal{L}(\boldsymbol{\theta}+\Delta\boldsymbol{\theta}) < \mathcal{L}(\boldsymbol{\theta})$。为此，我们考虑一阶展开：
\begin{equation}\mathcal{L}(\boldsymbol{\theta}+\Delta\boldsymbol{\theta})\approx \mathcal{L}(\boldsymbol{\theta}) + \langle \nabla_{\boldsymbol{\theta}}\mathcal{L}, \Delta\boldsymbol{\theta}\rangle \label{eq:approx-1}\end{equation}
假设这个近似的精度已经足够，那么$\mathcal{L}(\boldsymbol{\theta}+\Delta\boldsymbol{\theta}) < \mathcal{L}(\boldsymbol{\theta})$意味着$\langle \nabla_{\boldsymbol{\theta}}\mathcal{L}, \Delta\boldsymbol{\theta}\rangle < 0$，即更新量与梯度的夹角至少大于90度，而其中最自然的选择就是
\begin{equation}\Delta\boldsymbol{\theta} = -\eta \nabla_{\boldsymbol{\theta}}\mathcal{L}\end{equation}
这便是梯度下降，即更新量取梯度的反方向，其中$\eta > 0$即为学习率。

无一例外 #

回到多任务学习上，如果假设每个任务都同等重要，那么我们可以将这个假设理解为每一步更新的时候$\mathcal{L}_1,\mathcal{L}_2,\cdots,\mathcal{L}_n$都下降或保持不变。如果参数到达$\boldsymbol{\theta}^*$后，不管再怎么变化，都会导致某个$\mathcal{L}_i$上升，那么就说$\boldsymbol{\theta}^*$是帕累托最优解（Pareto Optimality）。说白了，帕累托最优意味着我们不能通过牺牲某个任务来换取另一个任务的提升，意味着任务之间没有相互“内卷”。

假设近似$\eqref{eq:approx-1}$依然成立，那么寻找帕累托最优意味着我们要寻找$\Delta\boldsymbol{\theta}$满足
\begin{equation}\left\{\begin{aligned}
&\langle \nabla_{\boldsymbol{\theta}}\mathcal{L}_1, \Delta\boldsymbol{\theta}\rangle \leq 0\\
&\langle \nabla_{\boldsymbol{\theta}}\mathcal{L}_2, \Delta\boldsymbol{\theta}\rangle \leq 0\\
&\quad \vdots \\
&\langle \nabla_{\boldsymbol{\theta}}\mathcal{L}_n, \Delta\boldsymbol{\theta}\rangle \leq 0\\
\end{aligned}\right.\end{equation}
注意到它存在平凡解$\Delta\boldsymbol{\theta}=\boldsymbol{0}$，所以上述不等式组的可行域肯定非空，我们主要关心可行域中是否存在非零解：如果有，则找出来作为更新方向；如果没有，则有可能已经达到了帕累托最优（必要不充分），我们称此时的状态为帕累托稳定点（Pareto Stationary）。

求解算法 #

方便起见，我们记$\boldsymbol{g}_i=\nabla_{\boldsymbol{\theta}}\mathcal{L}_i$，我们寻求一个向量$\boldsymbol{u}$，使得对所有的$i$都满足$\langle \boldsymbol{g}_i, \boldsymbol{u}\rangle \geq 0$，那么我们就可以像单任务梯度下降那样取$\Delta\boldsymbol{\theta}=-\eta\boldsymbol{u}$作为更新量。如果任务数只有两个，可以验证$\boldsymbol{u}=\boldsymbol{g}_1/\Vert\boldsymbol{g}_1\Vert + \boldsymbol{g}_2/\Vert\boldsymbol{g}_2\Vert$自动满足$\langle \boldsymbol{g}_1, \boldsymbol{u}\rangle \geq 0$和$\langle \boldsymbol{g}_2, \boldsymbol{u}\rangle \geq 0$，也就是说，双任务学习时，前面说的梯度归一化可以达到帕累托稳定点。

当任务数大于2时，问题开始变得有点复杂了，这里介绍两种求解方法，其中第一种思路是笔者自己给出的推导结果，第二种思路则是《Multi-Task Learning as Multi-Objective Optimization》给出的“标准答案”。

问题转化 #

首先我们对问题进行进一步的转化。留意到
\begin{equation}\forall i, \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle \geq 0\quad\Leftrightarrow\quad \min_i \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle \geq 0\label{eq:q-0}\end{equation}
所以我们只需要尽量最大化最小的那个$\langle \boldsymbol{g}_i, \boldsymbol{u}\rangle$，就能找出理想的$\boldsymbol{u}$，即问题变成了
\begin{equation}\max_{\boldsymbol{u}}\min_i \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle \end{equation}
不过这有点危险，因为一旦真的存在非零的$\boldsymbol{u}$使得$\min\limits_i \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle > 0$，那么让$\boldsymbol{u}$的模长趋于正无穷，那么最大值便会趋于正无穷。所以为了结果的稳定性，我们需要加个正则项，考虑
\begin{equation}\max_{\boldsymbol{u}}\min_i \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle - \frac{1}{2}\Vert \boldsymbol{u}\Vert^2\label{eq:q-1}\end{equation}
这样无穷大模长的$\boldsymbol{u}$就不可能是最优解了。注意到代入$\boldsymbol{u}=0$后有$\min\limits_i \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle - \frac{1}{2}\Vert \boldsymbol{u}\Vert^2=0$，所以假设对$\boldsymbol{u}$取$\max$的最优解为$\boldsymbol{u}^*$，那么必然有
\begin{equation}\min_i \langle \boldsymbol{g}_i, \boldsymbol{u}^*\rangle - \frac{1}{2}\Vert \boldsymbol{u}^*\Vert^2\geq 0\quad\Leftrightarrow\quad \min_i \langle \boldsymbol{g}_i, \boldsymbol{u}^*\rangle \geq \frac{1}{2}\Vert \boldsymbol{u}^*\Vert^2\geq 0\end{equation}
所以问题$\eqref{eq:q-1}$的解必然是满足条件$\eqref{eq:q-0}$的解，并且如果是非零解，那么其反方向必然是使得所有任务损失都下降的方向。

光滑近似 #

现在介绍问题$\eqref{eq:q-1}$的第一种求解方案，它假设读者像笔者一样不熟悉min-max问题的求解，那么我们可以将第一步的$\min$用光滑近似代替（参考《寻求一个光滑的最大值函数》），即
\begin{equation}\min_i \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle \approx -\frac{1}{\lambda}\log\sum_i e^{-\lambda \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle}\,\,\big(\text{对于足够大的}\lambda\big)\end{equation}
于是我们就可以先求解
\begin{equation}\max_{\boldsymbol{u}}-\frac{1}{\lambda}\log\sum_i e^{-\lambda \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle} - \frac{1}{2}\Vert \boldsymbol{u}\Vert^2\end{equation}
然后再让$\lambda\to\infty$。这样我们就将问题转化为了单个函数的无约束最大化问题，直接求梯度然后让梯度为零得到
\begin{equation}\frac{\sum\limits_i e^{-\lambda \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle} \boldsymbol{g}_i}{\sum\limits_i e^{-\lambda \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle}} = \boldsymbol{u}\end{equation}
假设各个$\langle \boldsymbol{g}_i, \boldsymbol{u}\rangle$的差距大于$\mathscr{O}(1/\lambda)$量级，那么当$\lambda\to\infty$时，上式实际上是
\begin{equation}\boldsymbol{u} = \boldsymbol{g}_{\tau},\quad \tau = \mathop{\arg\min}_i \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle\end{equation}
然而，如果直接按照$\boldsymbol{u}^{(k+1)} = \boldsymbol{g}_{\tau},\tau = \mathop{\arg\min}\limits_i \langle \boldsymbol{g}_i, \boldsymbol{u}^{(k)}\rangle$的格式迭代，那么大概率是会振荡的，因为它要我们找到让$\langle \boldsymbol{g}_i, \boldsymbol{u}^{(k)}\rangle$最小的$\boldsymbol{g}_i$作为$\boldsymbol{u}^{(k+1)}$，假设为$\boldsymbol{u}^{(k+1)}=\boldsymbol{g}_{i^*}$，那么下一步让$\langle \boldsymbol{g}_i, \boldsymbol{u}^{(k+1)}\rangle=\langle \boldsymbol{g}_i, \boldsymbol{g}_{i^*}\rangle$最小的$\boldsymbol{g}_i$就很可能不再是$\boldsymbol{g}_{i^*}$了，反而$\boldsymbol{g}_{i^*}$可能是最大的那个。

直观来想，上述算法虽然振荡，但应该也是围绕着最优点$\boldsymbol{u}^*$振荡的，所以如果我们把振荡过程中的所有结果都平均起来，就应该能得到最优点了，这意味着收敛到最优点的迭代格式是
\begin{equation}\boldsymbol{u}^{(k+1)} = \frac{k \boldsymbol{u}^{(k)} + \boldsymbol{g}_{\tau}}{k + 1},\quad \tau = \mathop{\arg\min}_i \langle \boldsymbol{g}_i, \boldsymbol{u}^{(k)}\rangle\label{eq:sol-1}\end{equation}
留意到每次叠加上去的都是某个$\boldsymbol{g}_i$，所以最终的$\boldsymbol{u}^*$必然是各个$\boldsymbol{g}_i$的加权平均，即存在$\alpha_1,\alpha_2,\cdots,\alpha_n\geq 0$且$\alpha_1 + \alpha_2 + \cdots + \alpha_n =1$，使得
\begin{equation}\boldsymbol{u}^* = \sum_i \alpha_i \boldsymbol{g}_i\end{equation}
我们也可以将$\alpha_1,\alpha_2,\cdots,\alpha_n$理解为各个$\mathcal{L}_i$的当前最优权重分配方案。

对偶问题 #

光滑近似技巧的好处是比较简单直观，不需要太多的优化算法基础，不过它终究只是“非主流”思路，有颇多不严谨之处（但结果倒是对的）。下面我们来介绍基于对偶思想的“标准答案”。

首先，定义$\mathbb{P}^n$为所有$n$元离散分布的集合，即
\begin{equation}\mathbb{P}^n = \left\{(\alpha_1,\alpha_2,\cdots,\alpha_n)\left|\alpha_1,\alpha_2,\cdots,\alpha_n\geq 0, \sum_i \alpha_i = 1\right.\right\}\end{equation}
那么容易检验
\begin{equation}\min_i \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle = \min_{\alpha\in\mathbb{P}^n}\left\langle \tilde{\boldsymbol{g}}(\alpha), \boldsymbol{u}\right\rangle,\quad \tilde{\boldsymbol{g}}(\alpha) = \sum_i \alpha_i \boldsymbol{g}_i\end{equation}
因此问题$\eqref{eq:q-1}$等价于
\begin{equation}\max_{\boldsymbol{u}}\min_{\alpha\in\mathbb{P}^n}\left\langle \tilde{\boldsymbol{g}}(\alpha), \boldsymbol{u}\right\rangle - \frac{1}{2}\Vert \boldsymbol{u}\Vert^2\label{eq:q-2}\end{equation}
上述函数关于$\boldsymbol{u}$是凹的，关于$\alpha$是凸的，并且$\boldsymbol{u},\alpha$的可行域都是凸集（集合中任意两点的加权平均仍然在集合中），所以根据冯·诺依曼的Minimax定理，式$\eqref{eq:q-2}$的$\min$和$\max$是可以交换的，即等价于
\begin{equation}\min_{\alpha\in\mathbb{P}^n}\max_{\boldsymbol{u}}\left\langle \tilde{\boldsymbol{g}}(\alpha), \boldsymbol{u}\right\rangle - \frac{1}{2}\Vert \boldsymbol{u}\Vert^2 = \min_{\alpha\in\mathbb{P}^n}\frac{1}{2}\left\Vert\tilde{\boldsymbol{g}}(\alpha)\right\Vert^2\label{eq:q-3}\end{equation}
等号右边是因为$\max$部分只是一个无约束的二次函数最大值问题，可以直接算出$\boldsymbol{u}^* = \tilde{\boldsymbol{g}}(\alpha)$，因此最后只剩下$\min$，问题变成了求$\boldsymbol{g}_1,\boldsymbol{g}_2,\cdots,\boldsymbol{g}_n$的一个加权平均，使得其模长最小。

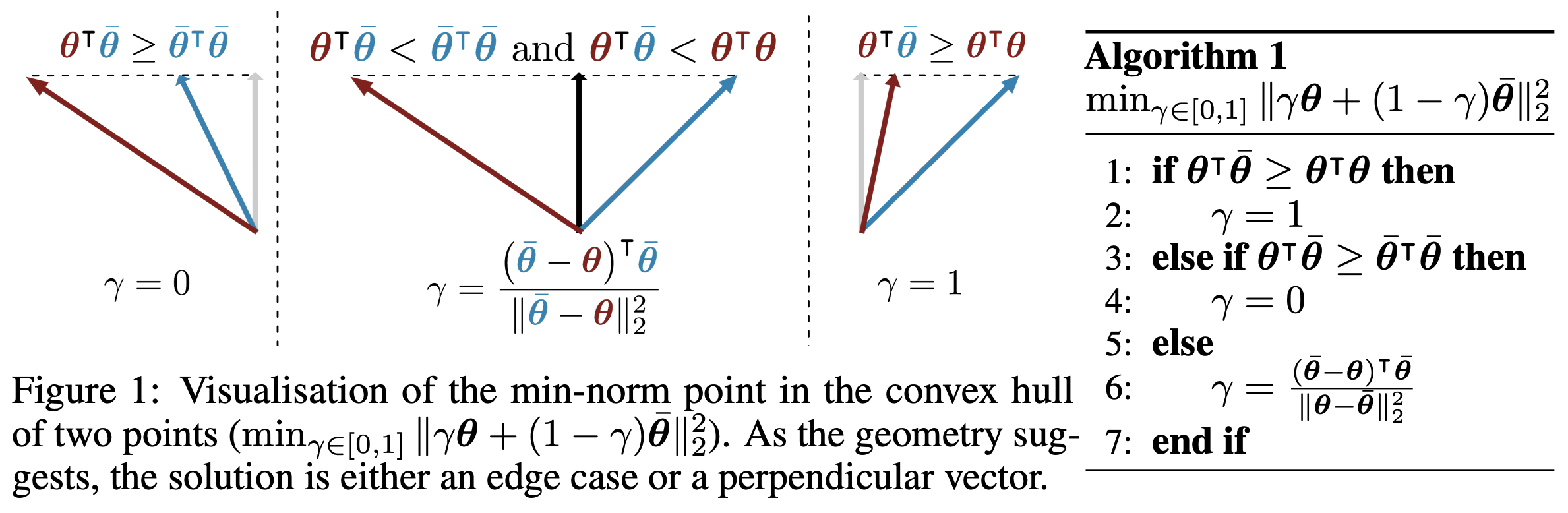
当$n=2$时，问题的求解比较简单，相当于作三角形的高，如下图所示：

当n=2时的求解算法及几何意义

当$n > 2$时，我们可以用Frank-Wolfe算法将它转化为多个$n=2$的情形进行迭代。对于Frank-Wolfe算法，我们可以将它理解为带约束的梯度下降算法，适合于参数的可行域为凸集的情形，但展开来介绍篇幅太大，这里就不详说了，请读者自行找资料学习。简单来说，Frank-Wolfe算法先通过线性化目标，找到下一步更新的方向为$e_{\tau}$，其中$\tau = \mathop{\arg\min}\limits_i \langle \boldsymbol{g}_i, \tilde{\boldsymbol{g}}(\alpha)\rangle$而$e_{\tau}$为$\tau$位置为1的one hot向量，然后求解在$\alpha$与$e_{\tau}$之间进行插值搜索，找出最优者作为迭代结果。所以，它的迭代过程为
\begin{equation}\left\{\begin{aligned}
&\tau = \mathop{\arg\min}_i \langle \boldsymbol{g}_i, \tilde{\boldsymbol{g}}(\alpha^{(k)})\rangle\\
&\gamma = \mathop{\arg\min}_{\gamma} \left\Vert\tilde{\boldsymbol{g}}((1-\gamma)\alpha^{(k)} + \gamma e_{\tau})\right\Vert^2 = \mathop{\arg\min}_{\gamma} \left\Vert(1-\gamma)\tilde{\boldsymbol{g}}(\alpha^{(k)}) + \gamma \boldsymbol{g}_{\tau}\right\Vert^2\\
&\alpha^{(k+1)} = (1-\gamma)\alpha^{(k)} + \gamma e_{\tau}
\end{aligned}\right.\end{equation}
其中$\gamma$的求解，正是$n=2$的特例，用上述截图中的算法即可。如果$\gamma$不通过搜索而得，而是固定为$1/(k+1)$，那么结果则等价于$\eqref{eq:sol-1}$，这也是Frank-Wolfe算法的一个简化版本。也就是说，我们通过光滑近似得到的结果，跟简化版Frank-Wolfe算法的结果是等价的。

去约束化 #

其实对于问题$\eqref{eq:q-3}$的求解，理论上我们也可以通过去约束的方式直接用梯度下降求解。比如直接设参数$\beta_1,\beta_2,\cdots,\beta_n\in\mathbb{R}$以及
\begin{equation}\alpha_i = \frac{e^{\beta_i}}{Z},\quad Z = \sum_i e^{\beta_i}\end{equation}
那么就可以转化为
\begin{equation}\min_{\beta} \frac{1}{2Z^2}\left\Vert \sum_i e^{\beta_i} \boldsymbol{g}_i\right\Vert^2\end{equation}
这是个无约束的优化问题，常规的梯度下降算法就可以求解。然而不知道为什么，笔者似乎没看到这样处理的（难道是不想调学习率？）。

一些技巧 #

在前一节中，我们给出了寻找帕累托稳定点的更新方向的两种方案，它们都要求我们在每一步的训练中，都要先通过另外的多步迭代来确定每个任务的权重，然后才能更新模型参数。由此不难想象，实际计算的时候计算量还是颇大的，所以我们需要想些技巧降低计算量。

梯度内积 #

可以看到，不管哪种方案，其关键步骤都有$\mathop{\arg\min}\limits_i \langle \boldsymbol{g}_i, \tilde{\boldsymbol{g}}(\alpha)\rangle$，这意味着我们要遍历梯度算内积。然而在深度学习场景下，模型参数量往往很大，所以梯度是一个非常大维度的向量，如果每一步迭代都要算一次内积，计算量很大。这时候我们可以利用展开式
\begin{equation}\langle \boldsymbol{g}_i, \tilde{\boldsymbol{g}}(\alpha)\rangle = \left\langle \boldsymbol{g}_i, \sum_j \alpha_j \boldsymbol{g}_j \right\rangle = \sum_j \alpha_j \langle \boldsymbol{g}_i, \boldsymbol{g}_j \rangle\end{equation}
每次迭代其实只有$\alpha$不同，所以其实在每一步训练中$\langle \boldsymbol{g}_i, \boldsymbol{g}_j \rangle$只需要计算一次存下来就行了，不用重复这种大维度向量内积的计算。

共享编码 #

然而，当模型大到一定程度的时候，要把每个任务的梯度都分别算出来然后进行迭代计算是难以做到的。如果我们假设多任务的各个模型共用同一个编码器，那么我们还可以进一步近似地简化算法。

具体来说，假设batch_size为$b$，第$j$个样本的编码输出为$\boldsymbol{h}_j$，那么由链式法则我们知道：
\begin{equation}\boldsymbol{g}_i = \nabla_{\boldsymbol{\theta}}\mathcal{L}_i = \sum_j (\nabla_{\boldsymbol{h}_j}\mathcal{L}_i)(\nabla_{\boldsymbol{\theta}}\boldsymbol{h}_j) = \underbrace{\big(\nabla_{\boldsymbol{h}_1}\mathcal{L}_i , \cdots , \nabla_{\boldsymbol{h}_b}\mathcal{L}_i\big)}_{\nabla_{\boldsymbol{H}}\mathcal{L}_i}\underbrace{\begin{pmatrix}\nabla_{\boldsymbol{\theta}}\boldsymbol{h}_b \\ \vdots \\ \nabla_{\boldsymbol{\theta}}\boldsymbol{h}_b\end{pmatrix}}_{\nabla_{\boldsymbol{\theta}}\boldsymbol{H}}\end{equation}
记$\boldsymbol{H} = (\boldsymbol{h}_1,\cdots,\boldsymbol{h}_b)$，那么就得到$\boldsymbol{g}_i = (\nabla_{\boldsymbol{H}}\mathcal{L}_i) (\nabla_{\boldsymbol{\theta}}\boldsymbol{H})$，利用矩阵范数不等式得到
\begin{equation}\left\Vert\sum_i \alpha_i \boldsymbol{g}_i\right\Vert^2 = \left\Vert\sum_i \alpha_i (\nabla_{\boldsymbol{H}}\mathcal{L}_i) (\nabla_{\boldsymbol{\theta}}\boldsymbol{H})\right\Vert^2 \leq \left\Vert\sum_i \alpha_i \nabla_{\boldsymbol{H}}\mathcal{L}_i\right\Vert^2 \big\Vert \nabla_{\boldsymbol{\theta}}\boldsymbol{H}\big\Vert^2 \end{equation}
不难想到，如果我们最小化$\left\Vert\sum\limits_i\alpha_i \nabla_{\boldsymbol{H}}\mathcal{L}_i\right\Vert^2$，那么计算量就会明显减少，因为这只需要我们对最后输出的编码向量的梯度，而不需要对全部参数的梯度。而上式告诉我们，最小化$\left\Vert\sum\limits_i\alpha_i \nabla_{\boldsymbol{H}}\mathcal{L}_i\right\Vert^2$实际上就是在最小化式$\eqref{eq:q-3}$的上界，像很多难以直接优化的问题一样，我们期望最小化上界也能获得类似的结果。

不过，这个上界虽然效率更高，但也有其局限性，它一般只适用于每一个样本都有多种标注信息的多任务学习，不适用于不同任务的训练数据无交集的场景（即每个任务是对不同的样本进行标注的，单个样本只有一种标注信息），因为对于后者来说，各个$\nabla_{\boldsymbol{H}}\mathcal{L}_i$是相互正交的，此时任务之间没有交互，上界没有体现出任务之间的相关性，也就是过于宽松而失去意义了。

错误证明 #

前面所提到的“标准答案”以及关于共享编码器时优化上界的结果，都来自论文《Multi-Task Learning as Multi-Objective Optimization》。接下来原论文试图证明当$\nabla_{\boldsymbol{\theta}}\boldsymbol{H}$满秩时，优化上界也能找到帕累托稳定点。但是很遗憾，原论文的证明是错误的。

证明位于原论文的附录A，里边用到了一个错误的结论：

如果$\boldsymbol{M}$是对称正定矩阵，那么$\boldsymbol{x}^{\top}\boldsymbol{y}\geq 0$当且仅当$\boldsymbol{x}^{\top}\boldsymbol{M}\boldsymbol{y}\geq 0$。

很容易举例证明该结论是错的，比如$\boldsymbol{x}=\begin{pmatrix}1 \\ -2\end{pmatrix},\boldsymbol{y}=\begin{pmatrix}1 \\ 1\end{pmatrix},\boldsymbol{M}=\begin{pmatrix}3 & 0\\ 0 & 1\end{pmatrix}$，此时$\boldsymbol{x}^{\top}\boldsymbol{y} < 0$但$\boldsymbol{x}^{\top}\boldsymbol{M}\boldsymbol{y} > 0$

经过思考，笔者认为原论文中的证明是难以修复的，即原论文的推测是不成立的，换言之，即便$\nabla_{\boldsymbol{\theta}}\boldsymbol{H}$满秩，优化上界得出的更新方向未必是能使得所有任务损失都不上升的方向，从而未必能找到帕累托稳定点。至于原论文中优化上界的实验效果也不错，只能说深度学习模型参数空间太大，可供“挪腾”的空间也很大，从而上界近似也能获得不错的结果了。

本文小结 #

在这篇文章中，我们从梯度的视角来理解多任务学习。在梯度视角下，多任务学习的主要工作是寻找一个尽可能与每个任务的梯度都反向的方向作为更新方向，从而使得每个任务的损失都能尽量下降，而不能通过牺牲某个任务来换取另一个任务的提升。这是任务之间无“内卷”的理想状态。

转载到请包括本文地址：https://spaces.ac.cn/archives/8896

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。