从DCGAN到SELF-MOD:GAN的模型架构发展一览
By 苏剑林 | 2019-04-19 | 100849位读者 |事实上,O-GAN的发现,已经达到了我对GAN的理想追求,使得我可以很惬意地跳出GAN的大坑了。所以现在我会试图探索更多更广的研究方向,比如NLP中还没做过的任务,又比如图神经网络,又或者其他有趣的东西。
不过,在此之前,我想把之前的GAN的学习结果都记录下来。
这篇文章中,我们来梳理一下GAN的架构发展情况,当然主要的是生成器的发展,判别器一直以来的变动都不大。还有,本文介绍的是GAN在图像方面的模型架构发展,跟NLP的SeqGAN没什么关系。
此外,关于GAN的基本科普,本文就不再赘述了。
话在前面 #
当然,从广义上来讲,图像领域的分类模型的任何进展,也算是判别器的进展(因为都是分类器,相关的技术都可能用到判别器中),而图像分类模型本质上从ResNet之后就没有质的变化,这也说明ResNet结构对判别器基本上是最优选择了。
但是生成器不一样,虽然从DCGAN之后GAN的生成器也形成了一些相对标准的架构设计,但远说不上定型,也说不上最优。直到最近也有不少工作在做生成器的新设计,比如SAGAN就是将Self Attention引入到了生成器(以及判别器)中,而大名鼎鼎的StyleGAN就是在PGGAN的基础上引入了一个风格迁移形式的生成器。
因此,很多工作都表明,GAN的生成器的结果还有一定的探索空间,好的生成器架构能加速GAN的收敛,或者提升GAN的效果。
DCGAN #
要谈到GAN架构发展史,肯定不得不说到DCGAN的,它在GAN史上称得上是一个标志性事件。
基本背景 #
众所周知,GAN起源于Ian Goodfellow的文章《Generative Adversarial Networks》中,但早期的GAN仅仅局限在MNIST这样的简单数据集中。这是因为GAN刚出来,虽然引起了一波人的兴趣,但依然还处于试错阶段,包括模型架构、稳定性、收敛性等问题都依然在探索中。而DCGAN的出现,为解决这一系列问题奠定了坚实的基础。
DCGAN出自文章《Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks》。要说它做了什么事情,其实也简单:它提出了一种生成器和判别器的架构,这个架构能极大地稳定GAN的训练,以至于它在相当长的一段时间内都成为了GAN的标准架构。
说起来简单,但事实上能做到这个事情很不容易,因为直观上“合理”的架构有很多,从各种组合中筛选出近乎最优的一种,显然是需要经过相当多的实验的。而正因为DCGAN几乎奠定了GAN的标准架构,所以有了DCGAN之后,GAN的研究者们可以把更多的精力放到更多样的任务之上,不再过多纠结于模型架构和稳定性上面,从而迎来了GAN的蓬勃发展。
架构描述 #
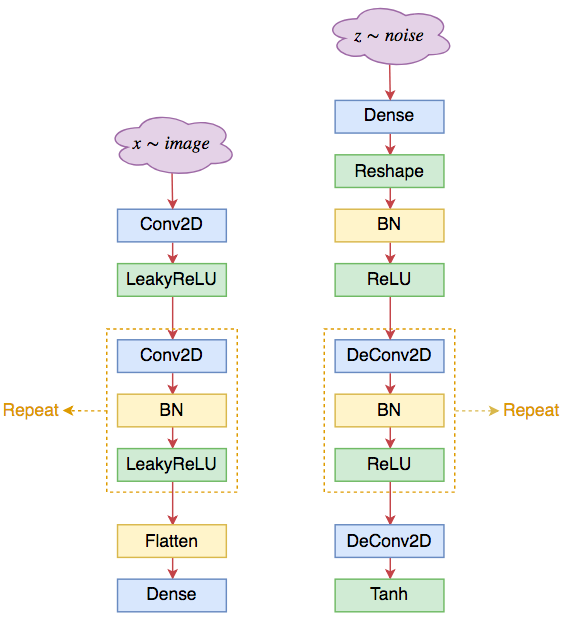
好了,说了这么多,我们回到架构本身的讨论之上。DCGAN所提出的模型架构大致如下:
1、生成器和判别器均不采用池化层,而采用(带步长的)的卷积层;其中判别器采用普通卷积(Conv2D),而生成器采用反卷积(DeConv2D);
2、在生成器和判别器上均使用Batch Normalization;
3、在生成器除输出层外的所有层上使用RelU激活函数,而输出层使用Tanh激活函数;
4、在判别器的所有层上使用LeakyReLU激活函数;
5、卷积层之后不使用全连接层;
6、判别器的最后一个卷积层之后也不用Global Pooling,而是直接Flatten
其实现在看来,这还是一种比较简单的结构,体现了大道至简的美感,进一步证明了好的必然是简洁的。
DCGAN的结构示意图如下:
个人总结 #
几个要点:
1、卷积和反卷积的卷积核大小为4*4或者5*5;
2、卷积和反卷积的stride一般都取为2;
3、对于判别器来说,第一层卷积后一般不用BN,而后面都是“Conv2D+BN+LeakyReLU”的组合模式,直到feature map的大小为4*4;
5、对于生成器来说,第一层是全连接,然后reshape为4*4大小,然后是“Conv2D+BN+ReLU”的组合模式,最后一层卷积则不用BN,改用tanh激活;相应地,输入图片都要通过除以255然后乘以2减去1,来缩放到-1~1之间。
虽然从参数量看可能很大,但事实上DCGAN很快,而且占显存不算多,所以很受大家欢迎。因此虽然看起来很老,但至今仍然很多任务都在用它。至少在快速实验上,它是一种优秀的架构。
ResNet #
随着GAN研究的日益深入,人们逐渐发现了DCGAN架构的一些不足之处。
DCGAN的问题 #
公认的说法是,由于DCGAN的生成器中使用了反卷积,而反卷积固有地存在“棋盘效应(Checkerboard Artifacts)”,这个棋盘效应约束了DCGAN的生成能力上限。关于棋盘效应,详细可以参考《Deconvolution and Checkerboard Artifacts》(强烈推荐,超多效果图示)。
准确来说,棋盘效应不是反卷积的问题,而是stride > 1的固有毛病,这导致了卷积无法“各向同性”地覆盖整张图片,而出现了交错效应,如同国际象棋的棋盘一般。而反卷积通常都要搭配stride > 1使用,因此通常认为是反卷积的问题。事实上,除了反卷积,膨胀卷积也会有棋盘效应,因为我们可以证明膨胀卷积在某种转化下,其实等价于stride > 1的普通卷积。
另一方面,笔者估计还有一个原因:DCGAN的非线性能力也许不足。分析过DCGAN结果的读者会留意到,如果输入的图片大小固定后,整个DCGAN的架构基本都固定的,包括模型的层数。唯一可以变化的似乎就只有卷积核大小(通道数也可以稍微调整,但其实调整空间不大),改变卷积核大小可以在一定程度上改变模型的非线性能力,但改变卷积核大小仅仅改变了模型的宽度,而对于深度学习来说深度可能比宽度更重要。问题就是对于DCGAN来说,没有一种自然而直接的方法来增加深度。
ResNet模型 #
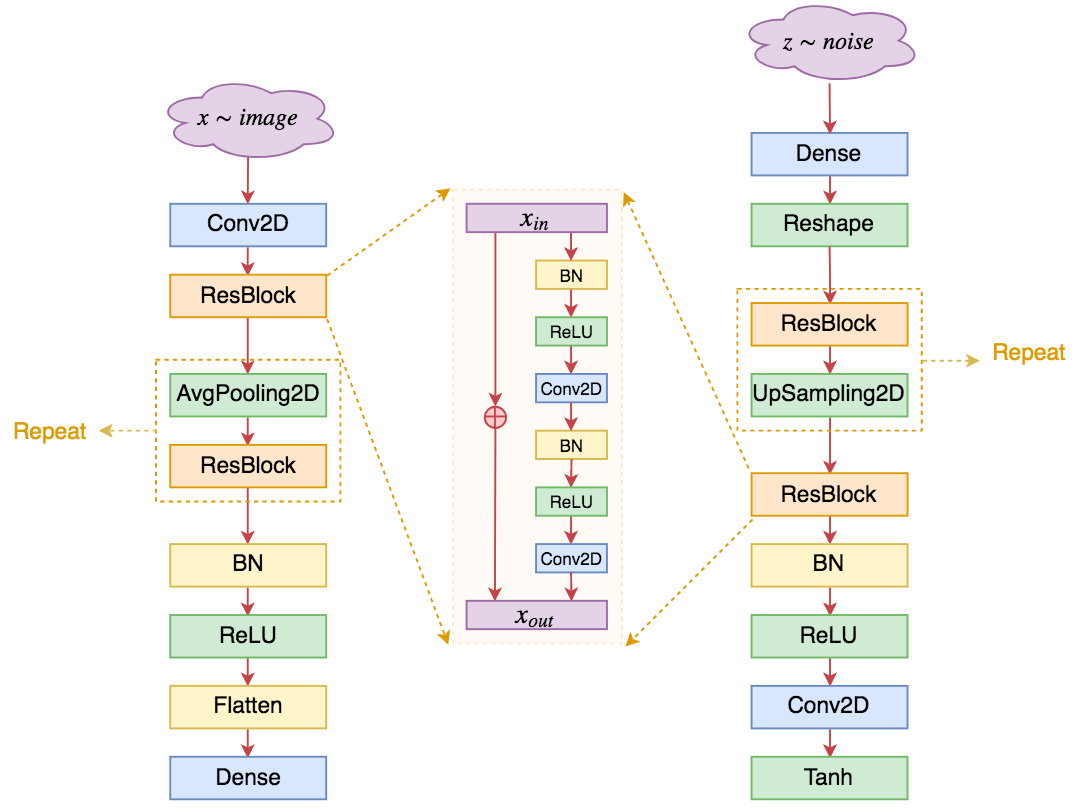
由于以上原因,并且随着ResNet在分类问题的日益深入,自然也就会考虑到ResNet结构在GAN的应用。事实上,目前GAN上主流的生成器和判别器架构确实已经变成了ResNet,基本结果图示如下:
可以看到,其实基于ResNet的GAN在整体结构上与DCGAN并没有太大差别(这进一步肯定了DCGAN的奠基作用),主要的特点在于:
1、不管在判别器还是生成器,均去除了反卷积,只保留了普通卷积层;
2、卷积核的大小通常统一使用3*3的,卷积之间构成残差块;
3、通过AvgPooling2D和UpSampling2D来实现上/下采样,而DCGAN中则是通过stride > 1的卷积/反卷积实现的;其中UpSampling2D相当于将图像的长/宽放大若干倍;
4、由于已经有残差,所以激活函数可以统一使用ReLU,当然,也有一些模型依然使用LeakyReLU,其实区别不大;
5、通过增加ResBlock的卷积层数,可以同时增加网络的非线性能力和深度,这也是ResNet的灵活性所在;
6、一般情况下残差的形式是$x+f(x)$,其中$f$代表卷积层的组合;不过在GAN中,模型的初始化一般要比常规分类模型的初始化更小,因此稳定起见,有些模型干脆将其改为$x+\alpha\times f(x)$,其中$\alpha$是一个小于1的数,比如0.1,这样能获得更好的稳定性;
7、有些作者认为BN不适合GAN,有时候会直接移除掉,或者用LayerNorm等代替。
个人总结 #
我没有认真考究过首先把ResNet用在GAN中是哪篇文章,只知道PGGAN、SNGAN、SAGAN等知名GAN都已经用上了ResNet。ResNet的stride都等于1,因此足够均匀,不会产生棋盘效应。
然而,ResNet并非没有缺点。虽然从参数量上看,相比DCGAN,ResNet并没有增加参数量,有些情况下甚至比DCGAN参数量更少,但ResNet比DCGAN要慢得多,所需要的显存要多得多。这是因为ResNet层数更多、层之间的连接更多,所以导致梯度更复杂,并且并行性更弱了(同一层卷积可以并行,不同层卷积是串联的,无法直接并行),结果就是更慢了,更占显存了。
还有,棋盘效应实际上是一种非常细微的效应,也许仅仅是在高清图生成时才能感受到它的差异,事实上在我的实验中,做128*128甚至256*256的人脸或LSUN生成,并没有明显目测到DCGAN和ResNet在效果上的差异,但是DCGAN的速度比ResNet快50%以上,在显存上,DCGAN可以直接跑到512*512的生成(单个1080ti),而ResNet的话,跑256*256都有些勉强。
因此,如果不是要PK目前的最优FID等指标,我都不会选择ResNet架构。
SELF-MOD #
正常来说,介绍完ResNet后,应该要介绍一下PGGAN、SAGAN等模型的,毕竟从分辨率或者IS、FID等指标上来看,它们也算是一个标志性事件。不过我并不打算介绍它们,因为严格来讲,PGGAN并不是一种新的模型架构,它只是提供了一个渐进式的训练策略,这种训练策略可以用到DCGAN或ResNet架构上;而SAGAN其实改动并不大,标准的SAGAN只不过在普通的DCGAN或ResNet架构中间,插入了一层Self Attention,不能算生成器架构上的大变动。
接下来介绍一个比较新的改进:Self Modulated Generator,来自文章《On Self Modulation for Generative Adversarial Networks》,我这里直接简称为“SELF-MOD”好了。
条件BN #
要介绍SELF-MOD之前,还需要介绍一个东西:Conditional Batch Normalization(条件BN)。
众所周知,BN是深度学习尤其是图像领域常见的一种操作。说实话我不大喜欢BN,但不得不说的是它在不少GAN模型中发挥了重要作用。常规的BN是无条件的:对于输入张量$\boldsymbol{x}_{i,j,k,l}$,其中$i,j,k,l$分别表示图像的batch、长、宽、通道维度,那么在训练阶段有
\begin{equation}\boldsymbol{x}_{i,j,k,l}^{(out)}=\boldsymbol{\gamma}_l \times \frac{\boldsymbol{x}_{i,j,k,l}^{(in)} - \boldsymbol{\mu}_l}{\boldsymbol{\sigma}_l+\epsilon} + \boldsymbol{\beta}_l\end{equation}
其中
\begin{equation}\boldsymbol{\mu}_l = \frac{1}{N}\sum_{i,j,k} \boldsymbol{x}_{i,j,k,l}^{(in)},\quad \boldsymbol{\sigma}^2_l = \frac{1}{N}\sum_{i,j,k} \left(\boldsymbol{x}_{i,j,k,l}^{(in)}-\boldsymbol{\mu}_l\right)^2\end{equation}
是输入批数据的均值方差,其中$N=\text{batch_size}\times \text{长}\times \text{宽}$,而$\boldsymbol{\beta},\boldsymbol{\gamma}$是可训练参数,$\epsilon$则是小的正常数,用来防止除零错误。除此之外,维护一组滑动平均变量$\hat{\boldsymbol{\mu}},\hat{\boldsymbol{\sigma}}^2$,在测试阶段的使用滑动平均的均值方差。
之所以说这样的BN是无条件的,是因为参数$\boldsymbol{\beta},\boldsymbol{\gamma}$纯粹由梯度下降得到,不依赖于输入。相应地,如果$\boldsymbol{\beta},\boldsymbol{\gamma}$依赖于某个输入$\boldsymbol{y}$,那么就称为条件BN:
\begin{equation}\boldsymbol{x}_{i,j,k,l}^{(out)}=\boldsymbol{\gamma}_l(\boldsymbol{y}) \times \frac{\boldsymbol{x}_{i,j,k,l}^{(in)} - \boldsymbol{\mu}_l}{\boldsymbol{\sigma}_l+\epsilon} + \boldsymbol{\beta}_l(\boldsymbol{y})\end{equation}
这时候$\boldsymbol{\beta}_l(\boldsymbol{y}),\boldsymbol{\gamma}(\boldsymbol{y})$是某个模型的输出。
先来说说怎么实现。其实在Keras中,实现条件BN非常容易,参考代码如下:
def ConditionalBatchNormalization(x, beta, gamma):
"""为了实现条件BN,只需要将Keras自带的BatchNormalization的
beta,gamma去掉,然后传入外部的beta,gamma即可;为了训练上的稳定,
beta最好能做到全0初始化,gamma最好能做到全1初始化。
"""
x = BatchNormalization(center=False, scale=False)(x)
def cbn(x):
x, beta, gamma = x
for i in range(K.ndim(x)-2):
# 调整beta的ndim,这个根据具体情况改动即可
beta = K.expand_dims(beta, 1)
gamma = K.expand_dims(gamma, 1)
return x * gamma + beta
return Lambda(cbn)([x, beta, gamma])SELF-MOD GAN #
条件BN首先出现在文章《Modulating early visual processing by language》中,后来又先后被用在《cGANs With Projection Discriminator》中,目前已经成为了做条件GAN(cGAN)的标准方案,包括SAGAN、BigGAN都用到了它。简单来说,cGAN就是把标签$\boldsymbol{c}$作为$\boldsymbol{\beta},\boldsymbol{\gamma}$的条件,然后构成条件BN,替换掉生成器的无条件BN。也就是说,生成器的主要输入还是随机噪声$\boldsymbol{z}$,然后条件$\boldsymbol{c}$则传入到生成器的每一个BN中。
说那么多条件BN,它跟SELF-MOD有什么关系呢?
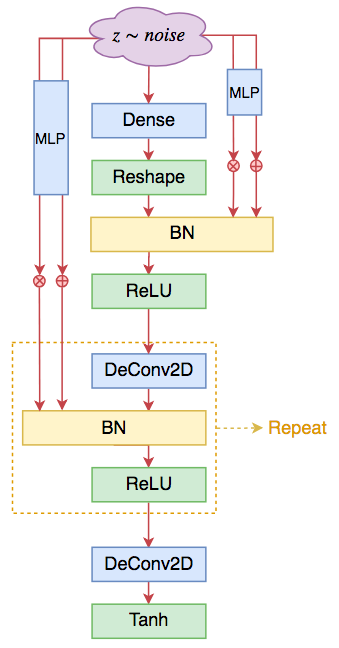
情况是这样的:SELF-MOD考虑到cGAN训练的稳定性更好,但是一般情况下GAN并没有标签$\boldsymbol{c}$可用,那怎么办呢?干脆以噪声$\boldsymbol{z}$自身为标签好了!这就是Self Modulated的含义了,自己调节自己,不借助于外部标签,但能实现类似的效果。用公式来描述就是
\begin{equation}\boldsymbol{x}_{i,j,k,l}^{(out)}=\boldsymbol{\gamma}_l(\boldsymbol{z}) \times \frac{\boldsymbol{x}_{i,j,k,l}^{(in)} - \boldsymbol{\mu}_l}{\boldsymbol{\sigma}_l+\epsilon} + \boldsymbol{\beta}_l(\boldsymbol{z})\end{equation}
在原论文中,$\boldsymbol{\beta}(\boldsymbol{z})$是两层全连接网络:
\begin{equation}\boldsymbol{\beta}(\boldsymbol{z})=\boldsymbol{W}^{(2)}\max\left(0, \boldsymbol{W}^{(1)}\boldsymbol{z}+\boldsymbol{b}^{(2)}\right)\end{equation}
$\boldsymbol{\gamma}(\boldsymbol{z})$也是一样的,而且看了下官方源代码,发现中间层的维度可以取得更小一些,比如32,这样不会明显增加参数量了。
这就是无条件GAN的SELF-MOD结构的生成器。
个人总结 #
我结合了自己的O-GAN实验了一下SELF-MOD结构,发现收敛速度几乎提升了50%,而且最终的FID和重构效果都更优一些,SELF-MOD的优秀可见一斑,而且隐隐有种感觉,似乎O-GAN与SELF-MOD更配(哈哈,不知道是不是自恋的错觉)。
Keras参考代码如下:
https://github.com/bojone/o-gan/blob/master/o_gan_celeba_sm_4x4.py
另外,哪怕在cGAN中,也可以用SELF-MOD结构。标准的cGAN是将条件$\boldsymbol{c}$作为BN的输入条件,SELF-MOD则是将$\boldsymbol{z}$和$\boldsymbol{c}$同时作为BN的输入条件,参考用法如下:
\begin{equation}\begin{aligned}\boldsymbol{\beta}(\boldsymbol{z},\boldsymbol{c}) =& \boldsymbol{W}^{(2)}\max\left(0, \boldsymbol{W}^{(1)}\boldsymbol{z}'+\boldsymbol{b}^{(2)}\right)\\
\boldsymbol{z}' =& \boldsymbol{z}+\text{E}(\boldsymbol{c})+\text{E}'(\boldsymbol{c})\otimes \boldsymbol{z}\end{aligned}\end{equation}
其中$\text{E},\text{E}'$是两个Embedding层,类别数比较少的情况下,直接理解为全连接层就行了,$\boldsymbol{\gamma}$同理。
其他架构 #
读者可能很奇怪,怎么还没谈到著名的BigGAN和StyleGAN?
事实上,BigGAN并没有做模型架构做出特别的改进,而且作者本身也承认这只不过是“暴力出奇迹”罢了;而对于StyleGAN,它确实改进了模型架构,但是理解了前面的SELF-MOD之后,其实也就不难理解StyleGAN了,甚至可以将StyleGAN看成是SELF-MOD的一个变种。
AdaIN #
StyleGAN的核心,是一个叫做AdaIN(Adaptive Instance Normalization)的玩意,来源于风格迁移的文章《Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization》。它其实跟条件BN差不多,甚至比条件BN还简单:
\begin{equation}\boldsymbol{x}_{i,j,k,l}^{(out)}=\boldsymbol{\gamma}_l(\boldsymbol{y}) \times \frac{\boldsymbol{x}_{i,j,k,l}^{(in)} - \boldsymbol{\mu}_{i,l}}{\boldsymbol{\sigma}_{i,l}+\epsilon} + \boldsymbol{\beta}_l(\boldsymbol{y})\end{equation}
跟条件BN的差别是:条件BN是$\boldsymbol{\mu}_{l}$和$\boldsymbol{\sigma}_{l}$,而AdaIN则是$\boldsymbol{\mu}_{i,l}$和$\boldsymbol{\sigma}_{i,l}$,也就是说AdaIN仅仅是在单个样本内部算统计特征,不需要用一批样本算,因此AdaIN也不用维护滑动平均的均值和方差,所以其实它比条件BN还简单。
StyleGAN #
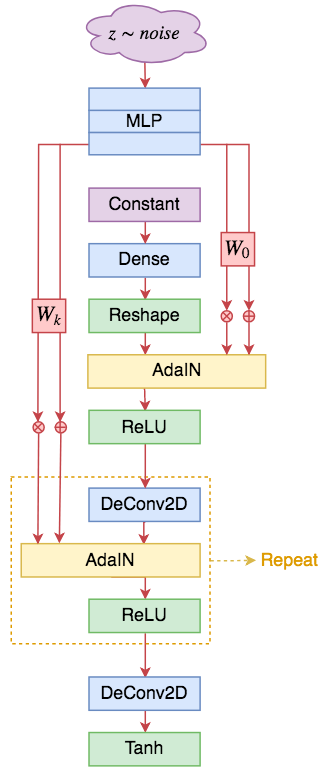
有了SELF-MOD和AdaIN后,其实就可以把StyleGAN说清楚了,StyleGAN的主要改动也就是生成器,相比于SELF-MOD,它的不同之处在于:
1、取消顶部的噪声输入,换成一个可训练的常数向量;
2、将所有条件BN换成AdaIN;
3、AdaIN的输入条件是将噪声用多层MLP变换后,再用不同的变换矩阵投影为不同AdaIN的$\boldsymbol{\beta}$和$\boldsymbol{\gamma}$。
就这么简单~
个人总结 #
我自己也实验过一个简化的StyleGAN形式的DCGAN,发现能收敛,效果也还行,但有轻微的Mode Collapse。由于官方的StyleGAN是用了PGGAN的模式进行训练的,而我没有,所以我猜测是不是StyleGAN要配合PGGAN才能训练好呢?目前还没有答案。只是在我的实验里,SELF-MOD要比StyleGAN好训练得多,效果也更好。
文章汇总 #
本文简单地梳理了一下GAN的模型架构变化情况,主要是从DCGAN、ResNet到SELF-MOD等变动,都是一些比较明显的改变,可能有些细微的改进就被忽略了。
一直以来,大刀阔斧地改动GAN模型架构的工作比较少,而SELF-MOD和StyleGAN则再次燃起了一部分人对模型架构改动的兴趣。《Deep Image Prior》这篇文章也表明了一个事实:模型架构本身所蕴含的先验知识,是图像生成模型可以成功的重要原因。提出更好的模型架构,意味着提出更好的先验知识,自然也就有利于图像生成了。
本文所提及的一些架构,都是经过自己实验过的,所作出评价都是基于自己的实验和审美观,如有不到位之处,请各位读者斧正~
转载到请包括本文地址:https://spaces.ac.cn/archives/6549
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Apr. 19, 2019). 《从DCGAN到SELF-MOD:GAN的模型架构发展一览 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/6549
@online{kexuefm-6549,
title={从DCGAN到SELF-MOD:GAN的模型架构发展一览},
author={苏剑林},
year={2019},
month={Apr},
url={\url{https://spaces.ac.cn/archives/6549}},
}











April 22nd, 2019
hello,博主,我看了大大的文章感触蛮深,我恰好对nlp比较感兴趣出, 大大觉得nlp现在什么方面值得做呀
April 23rd, 2019
请问博主,ResNet模块中通道数或feature map大小改变后,怎么让shortcut保持identity,有什么推荐好用的方法吗?
就是常规的通过1*1卷积改变通道数呀,但肯定不是identity了
May 11th, 2019
博主你好,我使用ResNet去训练GAN时,发现判别器的loss迅速降为0,而生成器loss居高不下,能否看下你是怎么训练的?如果可以的话能否分享一下?
有很多现成的结构和训练策略可以参考,比如我的ResNet GAN修改自:
https://github.com/LMescheder/GAN_stability
谢谢博主了
May 23rd, 2019
博主有用过Cycle-GAN和pix2pix吗,效果如何?
没有试过。
July 25th, 2019
这种仿射的条件模式真的很好用!做过个小测试,涉及全局推断的场景下,去掉自注意力,保留这个,效果也不会差多少。
对的
October 6th, 2019
typo?各项同性 => 各向同性
已经修正,感谢
July 2nd, 2020
我个人认为模型的结构关键是看模型的核心"零件",模型本身就是一个函数,只是其中部分子函数带参数要学习,部分函数没有带参数做一些平滑或者其他处理。
而模型结构的核心改进往往来源于一个想法,比如style-gan通过输入前段的多层全联接加强了输入z的表征能力,也保证了adin的风格变换,所有我理解style-gan前半段核心改进是加了全连接层来简化特征映射,后半段改进是用adin这个自适应单图特征来完成风格迁移。