再来一顿贺岁宴:从K-Means到Capsule
By 苏剑林 | 2018-02-12 | 282222位读者 |在本文中,我们再次对Capsule进行一次分析。
整体上来看,Capsule算法的细节不是很复杂,对照着它的流程把Capsule用框架实现它基本是没问题的。所以,困难的问题是理解Capsule究竟做了什么,以及为什么要这样做,尤其是Dynamic Routing那几步。
为什么我要反复对Capsule进行分析?这并非单纯的“炒冷饭”,而是为了得到对Capsule原理的理解。众所周知,Capsule给人的感觉就是“有太多人为约定的内容”,没有一种“虽然我不懂,但我相信应该就是这样”的直观感受。我希望尽可能将Capsule的来龙去脉思考清楚,使我们能觉得Capsule是一个自然、流畅的模型,甚至对它举一反三。
在《揭开迷雾,来一顿美味的Capsule盛宴》中,笔者先分析了动态路由的结果,然后指出输出是输入的某种聚类,这个“从结果到原因”的过程多多少少有些望文生义的猜测成分;这次则反过来,直接确认输出是输入的聚类,然后反推动态路由应该是怎样的,其中含糊的成分大大减少。两篇文章之间有一定的互补作用。
Capsule框架 #
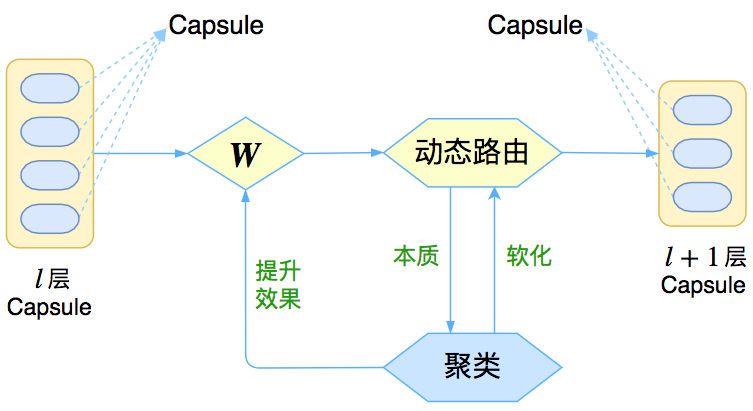
与其说Capsule是一个具体的模型,倒不如说Capsule是一个建模的框架,而框架内每个步骤的内容,是可以自己灵活替换的,而Hinton所发表的论文,只是一个使用案例。
这是一个怎样的框架呢?
特征表达 #
Capsule模型中,每个特征都是用一个向量(即Capsule,胶囊)来表示的。
当然,对于关注新闻的读者来说,这已经不是什么新消息。可能读者会有疑问:用向量来表示特征有什么稀奇的,本来神经网络的特征输入不就是一个向量吗?原来神经网络(MLP)的每一层输入是一个向量$\boldsymbol{x}\in\mathbb{R}^n$,然后输出是$\boldsymbol{y}=Activation(\boldsymbol{W}\boldsymbol{x}+\boldsymbol{b})\in \mathbb{R}^k$,我们就将$\boldsymbol{x}$的每一个分量都看成一个特征,那么每个特征都是标量了。而所谓的特征向量化后,那么每一层的输入变成了$\boldsymbol{x}\in\mathbb{R}^{n\times d_x}$,然后输出是$\boldsymbol{y}=Routing(\boldsymbol{x})\in \mathbb{R}^{k\times d_y}$,这时候的输入$\boldsymbol{x}$也看成是$n$个特征,但每个特征都是一个$d_x$维向量;输出$\boldsymbol{y}$则看成是$k$个特征,每个特征是一个$d_y$维向量。换一个角度看,其实就是说MLP每一层的输入输出由单个的向量变成了向量的集合(矩阵)。
或者我们可以将它换一个名称,叫做“特征的分布式表示”。也许有读者看到了“分布式表示”,会想起NLP中的词向量。没错,词向量一开始确实叫做“分布式表示”(Distributed Representation),而笔者看到Capsule的这一特点,第一反应也就是词向量。我们可以用词向量代替one hot来表示一个词,这样表达的信息就更为丰富了,而且所有的词都位于同一向量空间,方便后续处理。
此外,事实上图像中早也有这样的例子,众所周知彩色图像一般有RGB三个通道,每个通道256个选择,所以一共可以表达$256^3=16777216$种颜色(约1700万),为什么不直接用1700万个数字来分别表示这1700种颜色,而要分开3组,每组256个数字呢?这其实也是一种分布式表示,这样可以更好地表达色彩的多样性(比如红色的相近颜色是什么色?也许有人说橙色,也有人说紫色,也有可能是粉红,单一一个数字难以表达多种的相似性,而分组后则可以。)。更进一步说,我们在对图像不断进行卷积操作时,所得结果的通道维度,其实就是图像特征的一种分布式表示了。
特征组合 #
Capsule的第二个特点,是通过聚类来组合特征。
组合与表达 #
通过将底层特征组合为上层的特征,是跟我们的认知规律是相符的。在NLP中,我们有“字-->词-->句-->段”的层层组合;在图像中,我们也有“点-->线-->面-->体”的层层组合。面对新事物(上层特征),我们总会将它分解为我们熟悉的一些事物(底层特征),然后脑海里将这些事物映射到这个新事物(特征组合)。
对于我们来说,这个分解和组合的过程,不一定有什么目的,而只是为了用我们自己的方式去理解这个新事物(在大脑中形成良好的特征表达)。这也就能理解Hinton诟病深度学习、发展Capsule的原因之一了,因为他觉得现在深度学习的模型针对性太强(比如MNIST分类模型就只能做单个数字的识别,多个数字的识别就要重新构建数据集、重新设计并训练模型),而事实上,我们的根本目的并不是单纯地做任务,而是通过任务形成良好的、普适的特征表达,这样才有可能形成真正的人工智能。
特征间聚类 #
那么,怎么完成这个组合的过程呢?试想一下,两个字为什么能成为一个词,是因为这两个字经常“扎堆”出现,而且这个“堆”只有它们俩。这就告诉我们,特征的聚合是因为它们有聚类倾向,所以Capsule把聚类算法融入到模型中。
要注意,我们以前所说的聚类,都是指样本间的聚类,比如将MNIST的图片自动聚类成10个类别,或者将Word2Vec训练而来的词向量聚类成若干类,聚类的对象就是一个样本(输入)。而Capsule则设想将输入本身表示为若干个特征向量,然后对这些向量进行聚类(特征间的聚类),得到若干中心向量,接着再对这些中心向量聚类,层层递进,从而完成层层抽象的过程。这是一种特征间的聚类。
现在问题就来了。既然是聚类,是按照什么方法来聚类的呢?然后又是怎么根据这个聚类方法来导出那个神奇的Dynamic Routing的呢?后面我们会从K-Means出发来寻根问底,现在让我们先把主要思路讲完。
特征显著性 #
通过特征的组合可以得到上层特征,那如何对比特征的强弱程度呢?Capsule的答案是:模长。这就好比在茫茫向量如何找出“突出”的那个?只需要看看谁更高就行了。因此通过特征向量的模长来衡量它自己的“突出程度”,显然也是比较自然的选择。此外,一个有界的度量也是我们希望的,因此我们对特征向量做一个压缩:
$$squash(\boldsymbol{v})=\frac{\Vert\boldsymbol{v}\Vert^2}{1+\Vert\boldsymbol{v}\Vert^2}\frac{\boldsymbol{v}}{\Vert\boldsymbol{v}\Vert}\tag{1}$$
压缩的方案并不唯一,这里就不展开了。不过我在实验过程中,发现将1替换为0.5能提升性能。
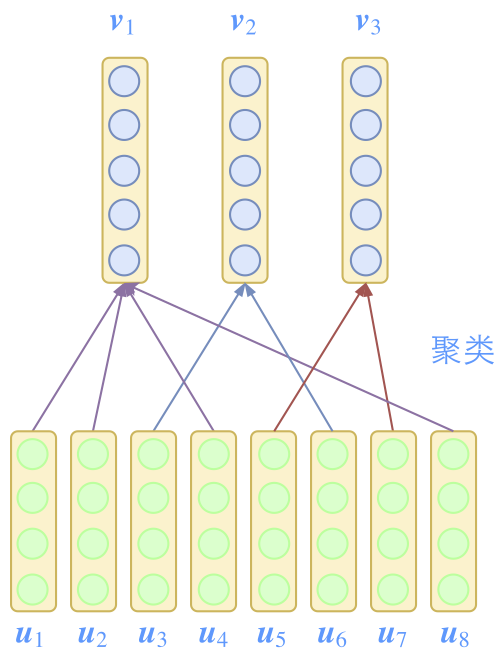
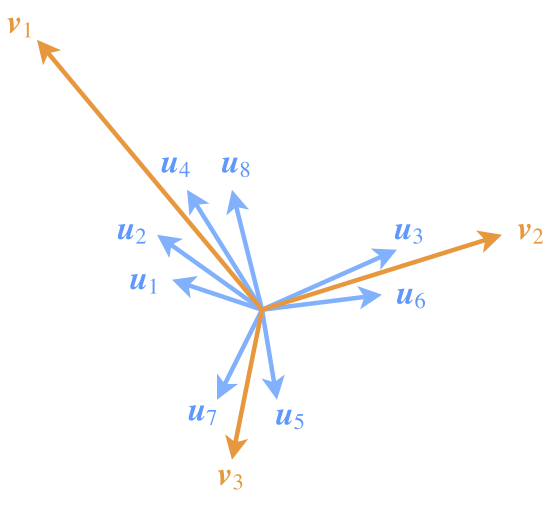
为了突出模长的这一含义,也需要在设计模型的时候有所配合。如图,尽管$\boldsymbol{v}_1$所代表的类所包含的特征向量$\boldsymbol{u}_1,\boldsymbol{u}_2,\boldsymbol{u}_4,\boldsymbol{u}_8$的模长均比较小,但因为成员多(“小弟多”),因此$\boldsymbol{v}_1$的模长也能占优(“势力大”)。这说明,一个类要突出,跟类内向量的数目、每个类内向量本身的模长都有关联。后面我们也会看到Capsule是如何体现这一点的。
K-Means新探 #
既然本文不断强调Capsule是通过聚类来抽象特征的,那么就有必要来细谈一下聚类算法了。Capsule所使用的聚类算法,其实是K-Means的变种。聚类算法有很多,理论上每种聚类算法都是可能的,然而要将聚类算法嵌入到Capsule中,还需要费上一点周折。
聚类目标 #
K-Means聚类本质上是一种“中心聚类方法”——聚类就是找类别中心。为了定义中心,我们就需要一个相近程度的度量,常用的是欧氏距离,但这并不是唯一的选择。所以这里我们干脆在一个更加一般的框架下介绍K-Means:K-Means希望把已有的数据$\boldsymbol{u}_1, \boldsymbol{u}_2, \dots, \boldsymbol{u}_n$无监督地划分为$k$类,聚类的方法是找出$k$个聚类中心$\boldsymbol{v}_1, \boldsymbol{v}_2, \dots, \boldsymbol{v}_k$,使得类内间隔最小:
$$L=\sum_{i=1}^n \min_{j=1}^k d(\boldsymbol{u}_i, \boldsymbol{v}_j)\tag{2}$$
这里$d$代表了相近程度的度量,所以这个式子的意思很简单,就是说每个$\boldsymbol{u}_i$只属于跟它最相近的那一类,然后将所有类内距离加起来,最小化这个类内距离:
$$(\boldsymbol{v}_1, \dots, \boldsymbol{v}_k) = \mathop{\text{argmin}}_{(\boldsymbol{v}_1, \dots, \boldsymbol{v}_k)}L\tag{3}$$
注:显然,聚类的结果依赖于$d$的具体形式,这其实就告诉我们:无监督学习和有监督学习的差别,在于我们跟模型“交流”的方法不同。有监督学习中,我们通过标注数据向模型传达我们的意愿;在无监督学习中,我们则通过设计适当的度量$d$来完成这个过程。
求解过程 #
怎么去最小化$L$来求出各个中心呢?如果读者不希望细细了解推导过程,可以跳过这一节,直接看下一节。
因为$L$中有$\min$这个操作,所以直接求它的梯度会有困难(不是不能求,而是在临界点附近不好处理),事实上有很多类似的问题没能得到很好的解决,都是因为它们的loss中有$\min$(日后有机会我们再谈这个事情。)。
然而,这里我们可以“软化”这个$L$,使得它可以求导。因为我们有一个很漂亮的公式(参考《寻求一个光滑的最大值函数》)
$$\begin{aligned}\max(\lambda_1,\lambda_2,\dots,\lambda_n)=&\lim_{K\to+\infty}\frac{1}{K}\ln\left(\sum_{i=1}^n e^{\lambda_i K}\right)\\
\approx&\frac{1}{K}\ln\left(\sum_{i=1}^n e^{\lambda_i K}\right)\end{aligned}\tag{4}$$
注:如果取$K=1$,显然括号里边就是softmax的分母,这也就是softmax的由来了——它是“soft”加“max”——“软的最大值”。
而我们有
$$\min(\lambda_1,\lambda_2,\dots,\lambda_n)=-\max(-\lambda_1,-\lambda_2,\dots,-\lambda_n)\tag{5}$$
因此我们就得到
$$L\approx-\frac{1}{K}\sum_{i=1}^n \ln\left(\sum_{j=1}^k e^{-K\cdot d(\boldsymbol{u}_i, \boldsymbol{v}_j)}\right)=-\frac{1}{K}\sum_{i=1}^n\ln Z_i\tag{6}$$
现在这个近似的loss在全局都光滑可导了。因此我们可以尝试求它的梯度
$$\frac{\partial L}{\partial \boldsymbol{v}_j}\approx\sum_{i=1}^n \frac{e^{-K\cdot d(\boldsymbol{u}_i, \boldsymbol{v}_j)}}{Z_i} \frac{\partial d(\boldsymbol{u}_i, \boldsymbol{v}_j)}{\partial \boldsymbol{v}_j}=\sum_{i=1}^n c_{ij}\frac{\partial d(\boldsymbol{u}_i, \boldsymbol{v}_j)}{\partial \boldsymbol{v}_j}\tag{7}$$
这里
$$c_{ij}=\mathop{softmax}\limits_j\Big(-K\cdot d(\boldsymbol{u}_i, \boldsymbol{v}_j)\Big)$$
我们已经指明了是对$j$所在的维度来归一化。为了求出一个极小值,我们希望让$\partial L/\partial \boldsymbol{v}_j=0$,但得到的方程并不是简单可解的。因此,可以引入一个迭代过程,假设$\boldsymbol{v}^{(r)}_j$是$\boldsymbol{v}_j$的第$r$次迭代的结果,那么我们可以让
$$0=\sum_{i=1}^n c_{ij}^{(r)}\frac{\partial d(\boldsymbol{u}_i, \boldsymbol{v}_j^{(r+1)})}{\partial \boldsymbol{v}_j^{(r+1)}}\tag{8}$$
如果可以从上述方程解出$\boldsymbol{v}_j^{(r+1)}$,那么就可以从中得到一个迭代格式。
欧氏距离 #
现在就可以把我们选择的度量代入$(8)$式进行计算了。我们可以看一个最基本的例子:$d(\boldsymbol{u}_i, \boldsymbol{v}_j)=\Vert\boldsymbol{u}_i - \boldsymbol{v}_j\Vert^2$,这时候就有
$$\frac{\partial d(\boldsymbol{u}_i, \boldsymbol{v}_j)}{\partial \boldsymbol{v}_j}=2(\boldsymbol{v}_j-\boldsymbol{u}_i)\tag{9}$$
根据$(8)$式得到$0=2\sum\limits_{i=1}^n c_{ij}^{(r)}\left(\boldsymbol{v}_j^{(r+1)}-\boldsymbol{u}_i\right)$,从而我们可以解出
$$v_{j}^{(r+1)}=\frac{\sum\limits_{i=1}^n c_{ij}^{(r)}\boldsymbol{u}_i}{\sum\limits_{i=1}^n c_{ij}^{(r)}}\tag{10}$$
如果取$K\to+\infty$,那么$c_{ij}^{(r)}$非0即1,所以上式就是说(读者可以自己把证明补充完整)
$\boldsymbol{v}_{j}^{(r+1)}$是距离$\boldsymbol{v}_{j}^{(r)}$最近的那些$\boldsymbol{u}_i$的平均值。
这就得到了我们平时说的K-Means聚类算法。
内积相似度 #
欧氏距离并不适合用在Capsule中,这是因为欧氏距离得到的中心向量是类内的向量的平均,这样类内向量越多,也不会导致中心向量的模越长,这不满足我们前面说的“小弟越多,势力越大”的设计。
什么距离比较适合呢?在论文《Dynamic Routing Between Capsules》中有一段话:
The initial coupling coefficients are then iteratively refined by measuring the agreement between the current output $\boldsymbol{v}_j$ of each capsule, $j$, in the layer above and the prediction $\boldsymbol{\hat{u}_{j|i}}$ made by capsule $i$.
The agreement is simply the scalar product $a_{ij} = \boldsymbol{v}_j \cdot \boldsymbol{\hat{u}_{j|i}}$ ...
对应到本文,大概的意思是用内积$\langle\boldsymbol{u}_i, \boldsymbol{v}_j\rangle$作为相似度的度量,也就是说,$d(\boldsymbol{u}_i, \boldsymbol{v}_j)=-\langle\boldsymbol{u}_i, \boldsymbol{v}_j\rangle$。但仔细思考就会发现问题,因为这样的$d$是无下界的!无下界的函数我们不能用来做loss,所以我一直被这里困惑着。直到有一天,我觉得可以将$\boldsymbol{v}_j$先归一化,然后再算内积,这样一来实际上是:
$$d(\boldsymbol{u}_i, \boldsymbol{v}_j)=-\left\langle\boldsymbol{u}_i, \frac{\boldsymbol{v}_j}{\Vert\boldsymbol{v}_j\Vert}\right\rangle\tag{11}$$
现在对于固定的$\boldsymbol{u}_i$,不管$\boldsymbol{v}_j$怎么变,$d(\boldsymbol{u}_i, \boldsymbol{v}_j)$就有下界了。所以这样的$d$是可以用来作为loss的,代入$(8)$式算,最终得到的结果是
$$\frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}=\frac{\sum\limits_{i=1}^n c_{ij}^{(r)}\boldsymbol{u}_i}{\left\Vert\sum\limits_{i=1}^n c_{ij}^{(r)}\boldsymbol{u}_i\right\Vert}\tag{12}$$
也就是说$\boldsymbol{v}_j^{(r+1)}$和$\sum\limits_{i=1}^n c_{ij}^{(r)}\boldsymbol{u}_i$的方向是一样的,但这不能说明它们两个是相等的。然而,这也意味着我们确实可以简单地取
$$\boldsymbol{v}_j^{(r+1)}=\sum\limits_{i=1}^n c_{ij}^{(r)}\boldsymbol{u}_i\tag{13}$$
如果取$K\to +\infty$的极限,那么就是说
$\boldsymbol{v}_{j}^{(r+1)}$是距离$\boldsymbol{v}_{j}^{(r)}$最近的那些$\boldsymbol{u}_i$的和。
由于现在是求和,就可以体现出“小弟越多,势力越大”的特点了。(注意,这里和欧氏距离那都出现了“最近”,两个最近的含义并不一样,因为所选用的$d$不一样。)
注:$(12)$式的推导过程。
$$\begin{aligned}\frac{\partial\left\langle\boldsymbol{u}_i, \frac{\boldsymbol{v}_j}{\Vert\boldsymbol{v}_j\Vert}\right\rangle}{\partial \boldsymbol{v}_j}=&\frac{\partial \left(\boldsymbol{u}_i \cdot \frac{\boldsymbol{v}_j}{\Vert\boldsymbol{v}_j\Vert}\right)}{\partial \boldsymbol{v}_j}\\
=&\frac{\boldsymbol{u}_i}{\Vert\boldsymbol{v}_j\Vert}+(\boldsymbol{u}_i \cdot \boldsymbol{v}_j)\frac{\partial}{\partial \boldsymbol{v}_j}\frac{1}{\Vert\boldsymbol{v}_j\Vert}\\
=&\frac{\boldsymbol{u}_i}{\Vert\boldsymbol{v}_j\Vert}-(\boldsymbol{u}_i \cdot \boldsymbol{v}_j)\frac{\boldsymbol{v}_j}{\Vert\boldsymbol{v}_j\Vert^3}\end{aligned}$$
然后根据$(8)$式,得到
$$0=\frac{\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}-\left(\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i \cdot \boldsymbol{v}_j^{(r+1)}\right)\frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert^3}$$
整理得
$$\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i=\left(\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i \cdot \frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\right)\frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}$$
两边取求模长
$$\left\Vert\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i\right\Vert=\left|\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i \cdot \frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\right|=\left\Vert\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i\right\Vert \times |\cos\theta|$$
这里的$\theta$是向量$\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i$和向量$\boldsymbol{v}_j^{(r+1)}$的夹角,上式表明$|\cos\theta|=1$,因此$\theta=0$或$\pi$,$\theta=\pi$事实上是极大值点而不是极小值,所以$\theta=0$,即它们方向一致,得到$(12)$式。
动态路由 #
经过漫长的准备,Dynamic Routing算法已经呼之欲出了。
按照第一部分,我们说Capsule中每一层是通过特征间聚类来完成特征的组合与抽象,聚类需要反复迭代,是一个隐式的过程。我们需要为每一层找到光滑的、显式的表达式$$\boldsymbol{v}_j=\boldsymbol{f}_j(\boldsymbol{u}_1,\dots,\boldsymbol{u}_n)\tag{14}$$ 才能完成模型的训练。动态路由就是通过迭代来写出这个(近似的)显式表达式的过程。
基本步骤 #
假设Capsule的输入特征分别为$\boldsymbol{u}_1, \boldsymbol{u}_2, \dots, \boldsymbol{u}_n$,然后下一层的特征向量就是$\boldsymbol{v}_1,\boldsymbol{v}_2,\dots,\boldsymbol{v}_k$,它就是前一层$n$个向量聚为$k$类的聚类中心,聚类的度量是前面的归一化内积,于是我们就可以写出迭代过程:
初始化$\boldsymbol{v}_{j} \leftarrow \boldsymbol{v}_{j}^{(0)}$
迭代$r$次:
$\boldsymbol{v}_{j} \leftarrow \boldsymbol{v}_{j}/\Vert\boldsymbol{v}_{j}\Vert$;
如果$j=\mathop{\text{argmax}}\limits_{j=1,\dots,k}\langle\boldsymbol{u}_i,\boldsymbol{v}_j\rangle$,那么$c_{ij} \leftarrow 1$,否则$c_{ij} \leftarrow 0$;
$\boldsymbol{v}_{j} \leftarrow \sum\limits_{i}c_{ij}\boldsymbol{u}_{i}$;
返回$squash(\boldsymbol{v}_j)$。
这个版本是容易理解,但由于存在$\text{argmax}$这个操作,我们用不了梯度下降,而梯度下降是目前求模型其他参数的唯一方法。为了解决这个问题,我们只好不取$K\to+\infty$的极限,取一个常数$K > 0$,然后将算法变为
初始化$\boldsymbol{v}_{j} \leftarrow \boldsymbol{v}_{j}^{(0)}$
迭代$r$次:
$\boldsymbol{v}_{j} \leftarrow \boldsymbol{v}_{j}/\Vert\boldsymbol{v}_{j}\Vert$;
$c_{ij} \leftarrow \mathop{softmax}\limits_j \Big(\langle\boldsymbol{u}_i,K\boldsymbol{v}_j\rangle\Big)$;
$\boldsymbol{v}_{j} \leftarrow \sum\limits_{i}c_{ij}\boldsymbol{u}_{i}$;
返回$squash(\boldsymbol{v}_j)$。
然而这样又新引入了一个参数$K$,咋看上去$K$太大了就梯度消失,$K$太小了就不够准确,很难确定。不过后面我们将会看到,直接让$K=1$即可,因为$K=1$的解空间已经包含了任意$K$的解。最终我们可以得到
初始化$\boldsymbol{v}_{j}=\boldsymbol{v}_{j}^{(0)}$
迭代$r$次:
$\boldsymbol{v}_{j} \leftarrow \boldsymbol{v}_{j}/\Vert\boldsymbol{v}_{j}\Vert$;
$c_{ij} \leftarrow \mathop{softmax}\limits_j \Big(\langle\boldsymbol{u}_i, \boldsymbol{v}_j\rangle\Big)$;
$\boldsymbol{v}_{j} \leftarrow \sum\limits_{i}c_{ij}\boldsymbol{u}_{i}$;
返回$squash(\boldsymbol{v}_j)$。
有意思的是,最后导出的结果,不仅跟Hinton的原始论文《Dynamic Routing Between Capsules》有所出入,跟我前一篇介绍也有出入。其中,最明显的差别是在迭代过程中用$\boldsymbol{v}_{j}/\Vert\boldsymbol{v}_{j}\Vert$替换了$squash(\boldsymbol{v}_j)$,仅在最后输出时才进行squash。实验表明这有助于提升特征的表达能力,它在我的前一文的数字实验(单数字训练,双数字预测)中,能达到95%以上的准确率(原来是91%)。
三种症状 #
这样就完了?远远还没有。我们还要解决好几个问题。
1、如何做好类别初始化? 因为聚类结果跟初始化有关,而且好的初始化往往是聚类成功的一大半。现在我们要将聚类这个过程嵌入到模型中,作为模型的一部分,那么各个$\boldsymbol{v}_{j}^{(0)}$应该怎么选取呢?如果同一初始化,那么无法完成聚类过程;如果随机初始化,那又不能得到确定的聚类结果(就算类中心向量不变,但是类的顺序也可能变化)。
2、如何识别特征顺序? 我们知道,聚类的结果跟样本的顺序是无关的,也就是说,如果将输入向量的顺序打乱,聚类的结果还是一样的。对于样本间的聚类,这是一个优点;然而如果是特征间的聚类,那么就有可能不妥了,因为不同顺序的特征组合可能代表不同的含义(就好比词序不同,句子含义也会不同),如果都给出一样的结果,那么就丧失了特征的序信息了;
3、如何保证特征表达能力? 动态路由将上层Capsule作为底层Capsule的聚类结果,每个类可能包含多个特征向量,但如果仅仅用类中心向量代表整个类的整体特征(上层特征),会不会降低了上层Capsule的特征表达能力?
一个对策 #
有意思的是,以上三个问题都可以由同一个方法解决:加变换矩阵。
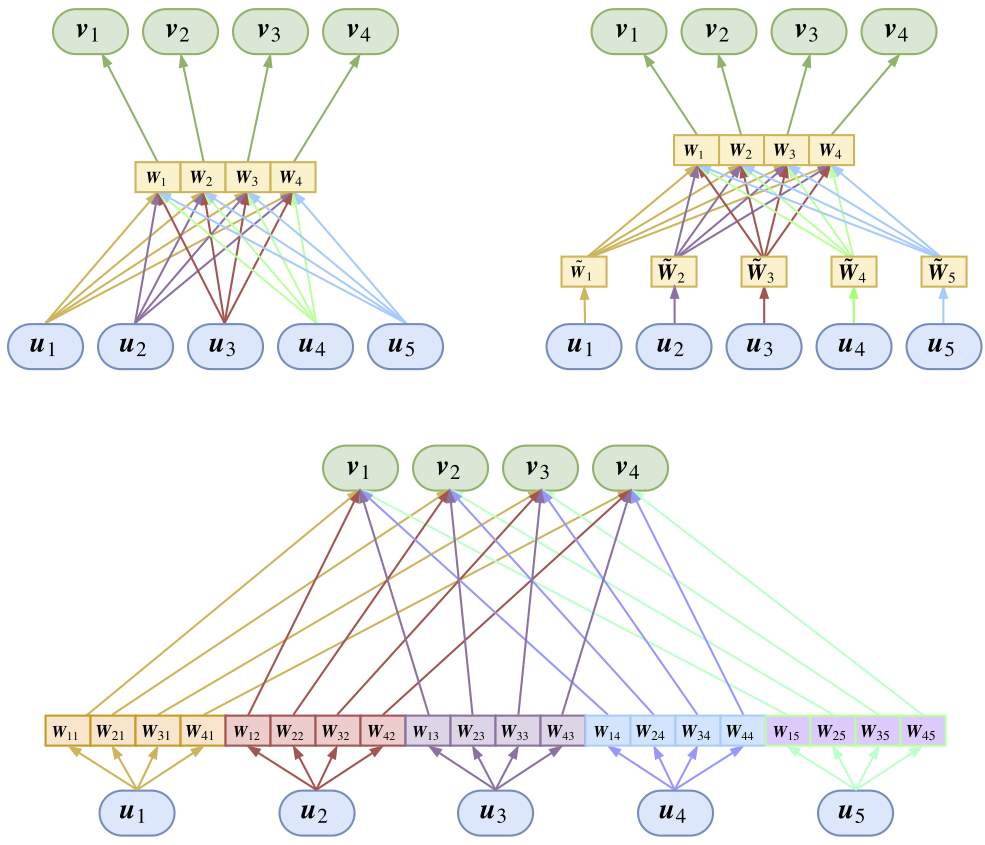
首先,为了模型的简洁性,我们将所有$\boldsymbol{u}_i$的和平均分配到每个类中作为$\boldsymbol{v}_j^{(0)}$。那怎么分辨出各个不同的类呢?我们在输出到每个类之前,给每个类都配一个变换矩阵$\boldsymbol{W}_j$,用来分辨不同的类,这时候动态路由变成了:
初始化$\boldsymbol{v}_{j} \leftarrow \frac{1}{k}\sum\limits_{i=1}^n\boldsymbol{W}_j\boldsymbol{u}_{i}$
迭代$r$次:
$\boldsymbol{v}_{j} \leftarrow \boldsymbol{v}_{j}/\Vert\boldsymbol{v}_{j}\Vert$;
$c_{ij} \leftarrow \mathop{softmax}\limits_j \Big(\langle\boldsymbol{W}_j\boldsymbol{u}_i, \boldsymbol{v}_j\rangle\Big)$;
$\boldsymbol{v}_{j} \leftarrow \sum\limits_{i}c_{ij}\boldsymbol{W}_j\boldsymbol{u}_{i}$;
返回$squash(\boldsymbol{v}_j)$。
这就是我前一篇介绍中所说的共享权重版的Capsule。细细斟酌就会发现,引入训练矩阵$\boldsymbol{W}_j$是个非常妙的招数,它不仅解决了聚类的初始化问题(同一初始化经过矩阵$\boldsymbol{W}_j$映射为不同初始化),而且通过$\boldsymbol{W}_j$可以改变$\boldsymbol{u}_i$的维度,从而也就改变了聚类后的中心向量的维度,这样也就能保证中心向量的特征表达能力(可以升高或降低维度)。还有,以前我们做分类,是用一个向量做内积然后softmax的方式,也就是用一个向量代表一个类,现在则相当于用一个矩阵来代表一个类,当然也就可以表达更丰富的类信息。此外还有一个好处,那就是我们有$\langle\boldsymbol{W}_j\boldsymbol{u}_i, K\boldsymbol{v}_j\rangle=\big\langle\big(K\boldsymbol{W}_j\big)\boldsymbol{u}_i, \boldsymbol{v}_j\big\rangle$,也就是说它相当于把前面的参数$K$也包含了,从而我们可以放心设$K=1$而不用担心准确性不够——如果有必要,模型会自己去调整$\boldsymbol{W}_j$达到调整$K$的效果!
现在只剩下最后一个问题了:识别输入特征的顺序。跟识别每一个类一样,我们也可以给每个输入都配一个变换矩阵$\boldsymbol{\tilde{W}}_i$,用来分辨不同位置的输入,这样一来动态路由变为
初始化$\boldsymbol{v}_{j} \leftarrow \frac{1}{k}\sum\limits_{i=1}^n\boldsymbol{W}_j\boldsymbol{\tilde{W}}_i\boldsymbol{u}_{i}$
迭代$r$次:
$\boldsymbol{v}_{j} \leftarrow \boldsymbol{v}_{j}/\Vert\boldsymbol{v}_{j}\Vert$;
$c_{ij} \leftarrow \mathop{softmax}\limits_j \Big(\langle\boldsymbol{W}_j\boldsymbol{\tilde{W}}_i\boldsymbol{u}_i, \boldsymbol{v}_j\rangle\Big)$;
$\boldsymbol{v}_{j} \leftarrow \sum\limits_{i}c_{ij}\boldsymbol{W}_j\boldsymbol{\tilde{W}}_i\boldsymbol{u}_{i}$;
返回$squash(\boldsymbol{v}_j)$。
如果觉得这样太累赘,那么可以把$\boldsymbol{W}_j\boldsymbol{\tilde{W}}_i$替换成一个整体矩阵$\boldsymbol{W}_{ji}$,也就是对每对指标$(i,j)$都配上一个变换矩阵,这样的好处是整体更简单明了,缺点是矩阵数目从$n+k$个变成了$nk$个:
初始化$\boldsymbol{v}_{j} \leftarrow \frac{1}{k}\sum\limits_{i=1}^n\boldsymbol{W}_{ji}\boldsymbol{u}_{i}$
迭代$r$次:
$\boldsymbol{v}_{j} \leftarrow \boldsymbol{v}_{j}/\Vert\boldsymbol{v}_{j}\Vert$;
$c_{ij} \leftarrow \mathop{softmax}\limits_j \Big(\langle\boldsymbol{W}_{ji}\boldsymbol{u}_i, \boldsymbol{v}_j\rangle\Big)$;
$\boldsymbol{v}_{j} \leftarrow \sum\limits_{i}c_{ij}\boldsymbol{W}_{ji}\boldsymbol{u}_{i}$;
返回$squash(\boldsymbol{v}_j)$。
这便是全连接版的动态路由。然而并不是每次我们都要分辨不同位置的输入,对于变长的输入,我们就很难给每个位置的输入都分配一个变换矩阵,这时候共享版的动态路由就能派上用场了。总的来说,全连接版和共享版动态路由都有其用武之地。
结语 #
笔者通过这两篇“浩浩荡荡”(哆里哆嗦)的博文,来试图解读Hinton大力发展的Capsule模型,然而作者水平有限,其中不当之处,还请读者海涵。
个人认为,Capsule的确是新颖的、有前景的的研究内容。也许它不一定(但也是有可能的)是未来的发展方向,但细细品味它,仍足以让我们获益良多。
现在回顾文章开头的目标——企图让Capsule看起来更加自然一些,不知道读者现在的感受如何?个人感觉是,之前经过这样的解析,Capsule也不是那么超然物外,而是一个大胆的尝试——Hinton大胆地将聚类的迭代过程融入到神经网络中,因此诞生了Capsule。
那是不是说,可以考虑将其他比较直观的算法也融入到里边,从而造就其他有意思的玩意?让我们拭目以待。
转载到请包括本文地址:https://spaces.ac.cn/archives/5112
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Feb. 12, 2018). 《再来一顿贺岁宴:从K-Means到Capsule 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/5112
@online{kexuefm-5112,
title={再来一顿贺岁宴:从K-Means到Capsule},
author={苏剑林},
year={2018},
month={Feb},
url={\url{https://spaces.ac.cn/archives/5112}},
}










March 29th, 2018
写的非常好,麻烦请教您一个问题,公式(4)的出处在哪里?
https://kexue.fm/archives/3290
April 2nd, 2018
初始化 $\boldsymbol{v}_j^{(0)}$ 时,有:
$\boldsymbol{v}_{j} \leftarrow \frac{1}{k}\sum\limits_{i=1}^n\boldsymbol{W}_j\boldsymbol{u}_{i}$
但是,你说“将所有$\boldsymbol{u}_i$的和平均分配到每个类中作为$\boldsymbol{v}_j^{(0)}$”, 那么是否上式应该为:
$\boldsymbol{v}_{j} \leftarrow \frac{1}{n}\sum\limits_{i=1}^n\boldsymbol{W}_j\boldsymbol{u}_{i}$
因为 ${k}$ 值代表向量$v$的类别数量呀。是我理解错了,还是你的笔误呢?
对于$L$层胶囊($n$个)来说,$L+1$层胶囊($k$个)是它的类,“平均分配到每个类”自然就是除以$k$。
April 2nd, 2018
$\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i=\left(\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i \cdot \frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\right)\frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}$
对上式两边求模,右边部分:
$$\left|\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i \cdot \frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\cdot\frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\right|
= \left\Vert\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i\right\Vert \cdot \left\Vert\frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\cdot\frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\right\Vert \cdot \cos\theta
$$
而下式是怎么把 $\left\Vert\frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\cdot\frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\right\Vert$ 这部分給约掉的呢?
$\left\Vert\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i\right\Vert=\left|\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i \cdot \frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\right|=\left\Vert\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i\right\Vert \times |\cos\theta|$
我的问题有点多,多谢一直以来苏兄的耐心解答,衷心感谢。
你把记号弄乱了。
我们来看对
$$\left(\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i \cdot \frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\right)\frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}$$
取模,注意$\left(\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i \cdot \frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\right)$是两个向量的内积,它是一个数而不是向量,所以这一项只需要加个绝对值,而$\frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}$才是个向量,而且是单位向量,所以模长为1,因此
$$\left\Vert\left(\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i \cdot \frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\right)\frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\right\Vert=\left|\sum\limits_{i=1}^n C_{ij}^{(r)}\boldsymbol{u}_i \cdot \frac{\boldsymbol{v}_j^{(r+1)}}{\left\Vert\boldsymbol{v}_j^{(r+1)}\right\Vert}\right|$$
然后再根据内积的定义:$\boldsymbol{a}\cdot\boldsymbol{b}=\Vert \boldsymbol{a}\Vert\times\Vert \boldsymbol{b}\Vert\times \cos\theta$算下去~
April 11th, 2018
看Hinton的文章,图像是叠加的,但是你的代码里面,图像时拼接的,后者准确率应该CNN就很高~
https://github.com/bojone/Capsule
#准备自定义的测试样本
#对测试集重新排序并拼接到原来测试集,就构成了新的测试集,每张图片有两个不同数字
idx = list(range(len(x_test)))
np.random.shuffle(idx)
X_test = np.concatenate([x_test, x_test[idx]], 1)
实验结果就是CNN+Pooling不高呀。
如果CNN+Pooling专门用这种数据集去训练,那么理论上也可以得到不错的准确率。然而现在考验的是“单数字训练,双数字测试”,测试集跟训练集不一致时,CNN+Pooling表现就欠佳了。
这个实验确实可以看成Hinton文章里边的重叠数字分离的简化版。
May 16th, 2018
乱七八糟写了一大堆,用的例子也不好,一个简简单单的东西被写的乱七八糟的,又是大盆菜又是小菜,胡扯什么呢.误导别人.根本没有真正理解这东西的原理就上来胡扯
你好,这毕竟只是个人博客,发表自己的观点用的。我又没收大家的钱。所以,觉得有需要就阅读,觉得是谬论就点击一下右上角的x就是了。
我倒是觉得,用大白话来聊聊学术的事情没什么不好的。举例不清,那就说“举例不清,没能说明xxx问题”;有错误,那就说“xxx部分,我认为有误,具体是xxxx”。
这种发牢骚再加人身攻击的评论,真的是乱七八糟写了一大堆,什么有用的话都没说。
May 18th, 2018
“但如果仅仅用类中心向量整个类的整体特征(上层特征)”应为“但如果仅仅用类中心向量代表整个类的整体特征(上层特征)”
已更正~
July 6th, 2018
您最终推导的动态路由步骤不是代码中的步骤吗?个人感觉这回推导把中间变量bij消去了
是我自己版本的动态路由。中间变量bij有没有显式写出来无关紧要的呀
August 12th, 2018
感觉聚类对动态路由的比拟还是挺有启发性的,不知道你有没有总结下发表论文?
October 7th, 2018
[...]再来一顿贺岁宴:从K-Means到Capsule[...]
October 9th, 2018
[...]再来一顿贺岁宴:从K-Means到Capsule[...]