科学空间|Scientific Spaces

我们考虑一个球状的星团，并假设它是各向同性的，即距离球心r处的物质密度ρ只与r有关，ρ=ρ(r)。那么，在半径为r的球形区域内的总质量为：
$$M(r)=\int_0^r 4\pi x^2 \rho(x) dx$$

想象有一颗质量比较小的恒星（其实相对于星团总质量，每一颗恒星的质量都很小）在星团的引力作用下运动（就好像太阳系绕着银河系运动一样），且恒星并没有受到其他物质（如星际尘埃等）的阻力。我们之前已经证明过，各向同性的球壳内部的引力是为0的，那么这种情况下的运动就相当于恒星只受到它到球心处的一个球形区域内的质量的引力吸引。根据万有引力定律，选择星团球心为参考系，可以得出
$$\ddot{\vec{r}}=-GM(r)\frac{\vec{r}}{r^3}$$

点击阅读全文...

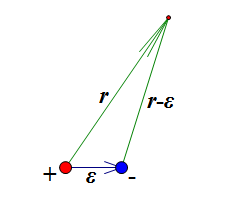
设想两个带有等量异号电荷的点电荷，它们之间的距离足够小，这样的一个模型被称为电偶极子（electric dipole）。我们研究电偶极子，主要是研究它在力学方面的性质。很多东西都可以用电偶极子来近似描述，比如一个小磁体周围的磁场，还有地球本身也可以近似看做一个偶极子来描述它的磁力情况，以及一些双原子分子的模型也被可以看做一个电偶极子模型，等等。在电偶极子模型中，两电荷的距离足够小，以至于我们忽略了一些关于距离的高次方项，只保留了线性部分，但对于物理探索来说，它已经足够精确，更重要的是，它足够简单，以至于我们可以容易把它清晰地描述出来。

我们先来研究电偶极子产生的电势。设它们各自的电荷量为q和-q，两者距离为ε，根据库仑定律，一个点电荷产生的电势，正比于该电荷的电荷量，同时反比于到该点电荷的距离。那么，一个电偶极子产生的电势为
$U=C(\frac{q}{r}+\frac{-q}{|\vec{r}-\vec{\varepsilon}|})$————(1)

点击阅读全文...

前边我承诺过会写一些关于自己对矩阵的理解。其实孟岩在《理解矩阵》这三篇文章中，已经用一种很直观的方法告诉了我们有关矩阵以及线性代数的一些性质和思想。而我对矩阵的理解，大多数也是来源于他的文章。当然，为了更好地理解线性代数，我还阅读了很多相关书籍，以求得到一种符合直觉的理解方式。孟岩的blog已经很久没有更新了，在此谨引用他的标题，来叙述我对矩阵的理解。

当然，我不打算追求那些空间、算子那些高抽象性的问题，我只是想发表一下自己对线性代数中一些常用工具的看法，比如说矩阵、行列式等。同时，文章命名为“理解矩阵”，也就是说这不是矩阵入门教程，而是与已经有一定的线性代数基础的读者一起探讨关于矩阵的其他理解方式，仅此而已。我估计基本上学过线性代数的读者都能够读懂这篇文章。

首先，我们不禁要追溯一个本源问题：矩阵是什么？

点击阅读全文...

上一篇文章中我从纯代数运算的角度来讲述了我对矩阵的一个理解，可以看到，我们赋予了矩阵相应的运算法则，它就在代数、分析等领域显示出了巨大作用。但是纯粹的代数是不足够的，要想更加完美，最好是找到相应的几何对象能够与之对应，只有这样，我们才能够直观地理解它，以达到得心应手的效果。

几何理解

我假设读者已经看过孟岩的《理解矩阵》三篇文章，所以更多的细节我就不重复了。我们知道，矩阵A

$$\begin{pmatrix}a_{11} & a_{12} \\ a_{21} & a_{22}\end{pmatrix}$$

事实上由两个向量$[a_{11},a_{21}]^T$和$[a_{12},a_{22}]^T$（这里的向量都是列向量）组成，它描述了一个平面（仿射）坐标系。换句话说，这两个向量其实是这个坐标系的两个基，而运算$y=Ax$则是告诉我们，在$A$这个坐标系下的x向量，在$I$坐标系下是怎样的。这里的$I$坐标系就是我们最常用的直角坐标系，也就是说，任何向量（包括矩阵里边的向量），只要它前面没有矩阵作用于它，那么它都是在直角坐标系下度量出来的。

点击阅读全文...

本文的最新版本位于：http://kexue.fm/archives/2208/

亲爱的读者朋友们，科学空间版的理解矩阵已经来到了BoJone认为是最激动人心的部分了，那就是关于行列式的叙述。这部分内容没有在孟岩的文章中被谈及到，是我自己结合了一些书籍和网络资源而得出的一些看法。其中最主要的书籍是《数学桥》，而追本溯源，促进我研究这方面的内容的是matrix67的那篇《教材应该怎么写》。本文包含了相当多的直观理解内容，在我看来，这部分内容也许不是正统的观点，但是至少在某种程度上能够促进我们对线性代数的理解。

大多数线性代数引入行列式的方式都是通过讲解线性方程组的，这种方式能够让学生很快地掌握它的计算，以及给出了一个最实际的应用（就是解方程组啦）。但是这很容易让读者走进一个误区，让他们认为线性代数就是研究解方程组的。这样并不能让读者真正理解到它的本质，而只有当我们对它有了一个直观熟练的感觉，我们才能很好地运用它。

行列式的出现其实是为了判断一个矩阵是否可逆的，它通过某些方式构造出一个“相对简单”的函数来达到这个目的，这个函数就是矩阵的行列式。让我们来反思一下，矩阵可逆意味着什么呢？之前已经提到过，矩阵是从一个点到另外一个点的变换，那么逆矩阵很显然就是为了把它变换回来。我们还说过，“运动是相对的”，点的变换又可以用坐标系的变换来实现。但是，按照我们的直觉，不同的坐标系除了有那些运算上的复杂度不同（比如一般的仿射坐标系计算点积比直角坐标系复杂）之外，不应该有其他的不同了，用物理的语言说，就是一切坐标系都是平权的。那么给出一个坐标系，可以自然地变换到另外一个坐标系，也可以自然地将它变换回来。既然矩阵是这种坐标系的一个描述，那么矩阵不可逆的唯一可能性就是：

这个$n$阶矩阵的$n$个列向量根本就构不成一个$n$维空间的坐标系。

点击阅读全文...

这篇文章估计是这个系列最后一篇了，也许以后会继续谈到线性代数，但是将会独立开来讲述。本文主要讲的是相似矩阵的一些事情，本文的观点很是粗糙，自己感觉都有点模糊，因此请读者细细阅读。在孟岩的文章里头，它对矩阵及其相似有了一个非常精彩的描述：

“矩阵是线性空间中的线性变换的一个描述。在一个线性空间中，只要我们选定一组基，那么对于任何一个线性变换，都能够用一个确定的矩阵来加以描述。”

同样的，对于一个线性变换，只要你选定一组基，那么就可以找到一个矩阵来描述这个线性变换。换一组基，就得到一个不同的矩阵。所有这些矩阵都是这同一个线性变换的描述，但又都不是线性变换本身。

点击阅读全文...

（阅读本文最好有一定的线性代数基础，至少对线性代数里边的基本概念有所了解。）

这学期已经接近尾声了，我们的《解析几何》已经讲到化简二次曲线了。可是，对于没有线性代数的其他同学们，直接用转轴和移轴这个计算公式来变换，那计算量会让我们很崩溃的；虽然那个“不变量”方法计算上有些简单，却总让人感到很诡异，总觉得不知从何而来，而且又要记一堆公式。事实上，如果有线性代数的基础，这些东西变得相当好理解的。我追求用统一的方法求解同一种问题，即用统一的方式处理所有的二次型，当然也希望计算量简单一点。

一般的模型

一般的二次型可以写成
$$x^T A x + 2 b^T x + c=0$$

其中$x,b$都是n维列向量（各元素为$x_i$和$b_i$），A是n阶方阵（各元素为$a_{ij}$），c是常数。在这里，我们只讨论n=2和n=3的情况。化简二次型的过程，可以归结为A矩阵的简化。

点击阅读全文...

我现在是越来越佩服爱因斯坦了，他的相对论是他天才的思想的充分体现。只有当相对论提出之后，宏观物理的大多数现象和规律才得到了统一的描述。狭义相对论中爱因斯坦对我们速度叠加常识的否定已经显示了他莫大的勇气，而一项头脑风暴性的工作——广义相对论则将他惊人的创造力体现得完美无瑕。我是被量子力学的数学吸引的，于相对论则是被相对论美妙的逻辑体系吸引。当然，其中也有相当美妙的数学。

狭义相对论中的核心内容之一就是被称为洛仑兹变换的东西，这在相对论发表之前已经由洛仑兹推导出来了，只不过他不承认他的物理意义，也就没有就此进行一次物理革命，革命的任务则由爱因斯坦完成。很久前我就已经看过洛仑兹变换的推导，那是直接设一种线性关系来求解的。但是我总感觉那样的推导不够清晰（也许是我的理解方式有问题吧），而且没有说明狭义相对论的两条原理如何体现出现。所以在研究过矩阵之后，我就尝试用矩阵来推导洛仑兹变换，发现效果挺好的，而且我觉得能够体现出相对论中的对称性。

两条原理

1、狭义相对性原理：在所有惯性系中，物理定律有相同的表达形式。这是力学相对性原理的推广，它适用于一切物理定律，其本质是所有惯性系平权。

2、光速不变原理：所有惯性系中，真空中的光速都等于c=299 792 458 m/s，与光源运动无关。迈克耳孙-莫雷实验是其有力证明。

点击阅读全文...