从loss的硬截断、软化到focal loss
By 苏剑林 | 2017-12-25 | 211850位读者 | 引用前言
今天在QQ群里的讨论中看到了focal loss,经搜索它是Kaiming大神团队在他们的论文《Focal Loss for Dense Object Detection》提出来的损失函数,利用它改善了图像物体检测的效果。不过我很少做图像任务,不怎么关心图像方面的应用。本质上讲,focal loss就是一个解决分类问题中类别不平衡、分类难度差异的一个loss,总之这个工作一片好评就是了。大家还可以看知乎的讨论:
《如何评价kaiming的Focal Loss for Dense Object Detection?》
看到这个loss,开始感觉很神奇,感觉大有用途。因为在NLP中,也存在大量的类别不平衡的任务。最经典的就是序列标注任务中类别是严重不平衡的,比如在命名实体识别中,显然一句话里边实体是比非实体要少得多,这就是一个类别严重不平衡的情况。我尝试把它用在我的基于序列标注的问答模型中,也有微小提升。嗯,这的确是一个好loss。
接着我再仔细对比了一下,我发现这个loss跟我昨晚构思的一个loss具有异曲同工之理!这就促使我写这篇博文了。我将从我自己的思考角度出发,来分析这个问题,最后得到focal loss,也给出我昨晚得到的类似的loss。
变分自编码器(二):从贝叶斯观点出发
By 苏剑林 | 2018-03-28 | 507930位读者 | 引用源起
前几天写了博文《变分自编码器(一):原来是这么一回事》,从一种比较通俗的观点来理解变分自编码器(VAE),在那篇文章的视角中,VAE跟普通的自编码器差别不大,无非是多加了噪声并对噪声做了约束。然而,当初我想要弄懂VAE的初衷,是想看看究竟贝叶斯学派的概率图模型究竟是如何与深度学习结合来发挥作用的,如果仅仅是得到一个通俗的理解,那显然是不够的。
所以我对VAE继续思考了几天,试图用更一般的、概率化的语言来把VAE说清楚。事实上,这种思考也能回答通俗理解中无法解答的问题,比如重构损失用MSE好还是交叉熵好、重构损失和KL损失应该怎么平衡,等等。
建议在阅读《变分自编码器(一):原来是这么一回事》后对本文进行阅读,本文在内容上尽量不与前文重复。
准备
在进入对VAE的描述之前,我觉得有必要把一些概念性的内容讲一下。
学会提问的BERT:端到端地从篇章中构建问答对
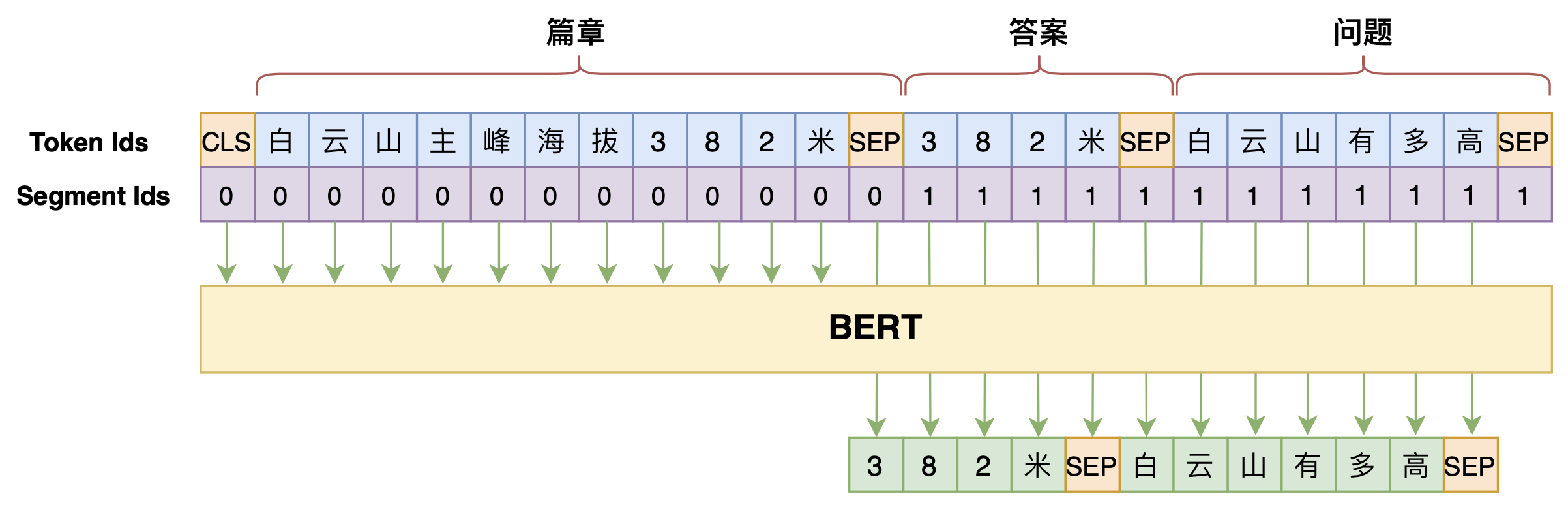
By 苏剑林 | 2020-07-25 | 128406位读者 | 引用机器阅读理解任务,相比不少读者都有所了解了,简单来说就是从给定篇章中寻找给定问题的答案,即“篇章 + 问题 → 答案”这样的流程,笔者之前也写过一些关于阅读理解的文章,比如《基于CNN的阅读理解式问答模型:DGCNN》等。至于问答对构建,则相当于是阅读理解的反任务,即“篇章 → 答案 + 问题”的流程,学术上一般直接叫“问题生成(Question Generation)”,因为大多数情况下,答案可以通过比较规则的随机选择,所以很多文章都只关心“篇章 + 答案 → 问题”这一步。
本文将带来一次全端到端的“篇章 → 答案 + 问题”实践,包括模型介绍以及基于bert4keras的实现代码,欢迎读者尝试。
【搜出来的文本】⋅(二)从MCMC到模拟退火
By 苏剑林 | 2021-01-14 | 56783位读者 | 引用在上一篇文章中,我们介绍了“受限文本生成”这个概念,指出可以通过量化目标并从中采样的方式来无监督地完成某些带条件的文本生成任务。同时,上一篇文章还介绍了“重要性采样”和“拒绝采样”两个方法,并且指出对于高维空间而言,它们所依赖的易于采样的分布往往难以设计,导致它们难以满足我们的采样需求。
此时,我们就需要引入采样界最重要的算法之一“Markov Chain Monte Carlo(MCMC)”方法了,它将马尔可夫链和蒙特卡洛方法结合起来,使得(至少理论上是这样)我们从很多高维分布中进行采样成为可能,也是后面我们介绍的受限文本生成应用的重要基础算法之一。本文试图对它做一个基本的介绍。
马尔可夫链
马尔可夫链实际上就是一种“无记忆”的随机游走过程,它以转移概率p(\boldsymbol{y}\leftarrow\boldsymbol{x})为基础,从一个初始状态\boldsymbol{x}_0出发,每一步均通过该转移概率随机选择下一个状态,从而构成随机状态列\boldsymbol{x}_0, \boldsymbol{x}_1, \boldsymbol{x}_2, \cdots, \boldsymbol{x}_t, \cdots ,我们希望考察对于足够大的步数t,\boldsymbol{x}_t所服从的分布,也就是该马尔可夫链的“平稳分布”。
从局部到全局:语义相似度的测地线距离
By 苏剑林 | 2022-12-07 | 36793位读者 | 引用前段时间在最近的一篇论文《Unsupervised Opinion Summarization Using Approximate Geodesics》中学到了一个新的概念,叫做“测地线距离(Geodesic Distance)”,感觉有点意思,特来跟大家分享一下。
对笔者来说,“新”的不是测地线距离概念本身(以前学黎曼几何的时候就已经接触过了),而是语义相似度领域原来也可以巧妙地构造出测地线距离出来,并在某些场景下发挥作用。如果乐意,我们还可以说这是“流形上的语义相似度”,是不是瞬间就高级了不少?
论文梗概
首先,我们简单总结一下原论文的主要内容。顾名思义,论文的主题是摘要,通常我们的无监督摘要是这样做的:假设文章由n个句子t_1,t_2,\cdots,t_n组成,给每个句子设计打分函数s(t_i)(经典的是tf-idf及其变体),然后挑出打分最大的若干个句子作为摘要。当然,论文做的不是简单的摘要,而是“Opinion Summarization”,这个“Opinion”,我们可以理解为实现给定的主题或者中心c,摘要应该倾向于抽取出与c相关的句子,所以打分函数应该还应该跟c有关,即s(t_i, c)。
从马尔科夫过程到主方程(推导过程)
By 苏剑林 | 2017-10-06 | 79722位读者 | 引用主方程(master equation)是对随机过程进行建模的重要方法,它代表着马尔科夫过程的微分形式,我们的专业主要工具之一就是主方程,说宏大一点,量子力学和统计力学等也不外乎是主方程的一个特例。
然而,笔者阅读了几个著作,比如《统计物理现代教程》,还有我导师的《生物系统的随机动力学》,我发现这些著作对于主方程的推导都很模糊,他们在着力解释结果的意义,但并不说明结果的思想来源,因此其过程难以让人信服。而知乎上有人提问《如何理解马尔科夫过程的主方程的推导过程?》但没有得到很好的答案,也表明了这个事实。
马尔可夫过程
主方程是用来描述马尔科夫过程的,而马尔科夫过程可以理解为运动的无记忆性,说通俗点,就是下一刻的概率分布,只跟当前时刻有关,跟历史状态无关。用概率公式写出来就是(这里只考虑连续型概率,因此这里的p是概率密度):
\begin{equation}\label{eq:maerkefu}p(x,\tau)=\int p(x,\tau|y,t) p(y,t) dy\end{equation}
这里的积分区域是全空间。这里的p(x,\tau|y,t)称为跃迁概率,即已经确定了t时刻来到了y位置后、在\tau时刻达到x的概率密度,这个式子的物理意义是很明显的,就不多做解释了。
如何“扒”站?手把手教你爬百度百科~
By 苏剑林 | 2017-05-17 | 34602位读者 | 引用从Wasserstein距离、对偶理论到WGAN
By 苏剑林 | 2019-01-20 | 231805位读者 | 引用2017年的时候笔者曾写过博文《互怼的艺术:从零直达WGAN-GP》,从一个相对通俗的角度来介绍了WGAN,在那篇文章中,WGAN更像是一个天马行空的结果,而实际上跟Wasserstein距离没有多大关系。
在本篇文章中,我们再从更数学化的视角来讨论一下WGAN。当然,本文并不是纯粹地讨论GAN,而主要侧重于Wasserstein距离及其对偶理论的理解。本文受启发于著名的国外博文《Wasserstein GAN and the Kantorovich-Rubinstein Duality》,内容跟它大体上相同,但是删除了一些冗余的部分,对不够充分或者含糊不清的地方作了补充。不管怎样,在此先对前辈及前辈的文章表示致敬。
(注:完整理解本文,应该需要多元微积分、概率论以及线性代数等基础知识。还有,本文确实长,数学公式确实多,但是,真的不复杂、不难懂,大家不要看到公式就吓怕了~)









最近评论