不知道大家留意到一个细节没有，就是当前NLP主流的预训练模式都是在一个固定长度（比如512）上进行，然后直接将预训练好的模型用于不同长度的任务中。大家似乎也没有对这种模式有过怀疑，仿佛模型可以自动泛化到不同长度是一个“理所应当”的能力。

当然，笔者此前同样也没有过类似的质疑，直到前几天笔者做了Base版的GAU实验后才发现GAU的长度泛化能力并不如想象中好。经过进一步分析后，笔者才明白原来这种长度泛化的能力并不是“理所当然”的......

模型回顾 #

在《FLASH：可能是近来最有意思的高效Transformer设计》中，我们介绍了“门控注意力单元GAU”，它是一种融合了GLU和Attention的新设计。

除了效果，GAU在设计上给我们带来的冲击主要有两点：一是它显示了单头注意力未必就逊色于多头注意力，这奠定了它“快”、“省”的地位；二是它是显示了注意力未必需要Softmax归一化，可以换成简单的$\text{relu}^2$除以序列长度：
\begin{equation}\boldsymbol{A}=\frac{1}{n}\text{relu}^2\left(\frac{\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}}{\sqrt{s}}\right)=\frac{1}{ns}\text{relu}^2\left(\mathcal{Q}(\boldsymbol{Z})\mathcal{K}(\boldsymbol{Z})^{\top}\right)\end{equation}
这个形式导致了一个有意思的问题：如果我们预训练的时候尽量将样本整理成同一长度（比如512），那么在预训练阶段$n$几乎一直就是512，也就是说$n$相当于一个常数，如果我们将它用于其他长度（比如64、128）微调，那么这个$n$究竟要自动改为样本长度，还是保持为512呢？

直觉应该是等于样本长度更加自适应一些，但答案很反直觉：$n$固定为512的微调效果比$n$取样本长度的效果要明显好！这就引人深思了......

问题定位 #

如果单看GAU的预训练效果，它是优于标准Attention的，所以GAU本身的拟合能力应该是没问题的，只是$\frac{1}{n}\text{relu}^2(\cdot)$在样本长度方面的迁移能力不好。为了确认这一点，笔者也尝试了混合不同长度的样本来做GAU的预训练，发现结果会有明显的改善。

那么，可能是GAU的什么地方出了问题呢？其实这不难猜测，GAU的整体运算可以简写成$\boldsymbol{O}=(\boldsymbol{U}\odot\boldsymbol{A}\boldsymbol{V})\boldsymbol{W}_o$，其中$\boldsymbol{U},\boldsymbol{V},\boldsymbol{W}_o$都是token-wise的，也就是说它们根本不会受到长度变化的影响，所以问题只能是出现在$\boldsymbol{A}$中。

以前我们用标准的Attention时，并没有出现类似的问题，以至于我们以前都无意识地觉得这是一个“理所当然”的性质。所以，我们需要从GAU的Attention与标准Attention的差异中发现问题。前面说了，两者不同的地方有两点，其一是多头Attention变成单头Attention，但是这顶多会让效果有一定波动，而我们测出来的结果是大幅下降，所以问题就只能出现在另一点，也就是归一化方式上，即Attention的$softmax$换成$\frac{1}{n}\text{relu}^2(\cdot)$所带来的。

验证这个猜测很简单，笔者将GAU中Attention的归一化方式换回Softmax后重新训练一个GAU模型，然后微调测试不同长度的任务，发现其效果比$\frac{1}{n}\text{relu}^2(\cdot)$时明显要好。所以，我们得出结论：Attention还是与Softmax更配～

原因分析 #

为什么更符合直觉的、自适应长度的$n$反而表现不如固定的$n$呢？既然我们已经以往用Softmax是没有这个问题的，所以我们不妨从Softmax出发找找灵感。Softmax的操作是：
\begin{equation}a_{i,j} = \frac{1}{Z_i}\exp\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right),\quad Z_i = \sum_{j=1}^n \exp\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right)\end{equation}
一个直接的问题就是：$Z_i$跟$n$的关系是怎样的呢？如果真有$Z_i=\mathcal{O}(n)$，那么理论上将$Z_i$换成$n$应该能取得相近的效果，至少不会是特别差的那种。

然而，我们知道注意力的重点是“注意”，它应该有能力“聚焦”到它认为比较重要的几个token上。同时，以往关于高效Transformer的一些实验结果显示，把标准Attention换成Local Attention后结果并不会明显下降，所以我们可以预计位置为$i$的Attention基本上就聚焦在$i$附近的若干token上，超出一定距离后就基本为0了。事实上，也有很多事后的可视化结果显示训练好的Attention矩阵其实是很稀疏的。

综合这些结果，我们可以得出，存在某个常数$k$，使得$|j-i|\geq k$时$\exp\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right)$都相当接近于0，这样一来$Z_i$应该更接近$\mathcal{O}(k)$而不是$\mathcal{O}(n)$，这就意味着$Z_i$很可能跟$n$是无关的，或者说跟$n$的数量级关系至少是小于$\mathcal{O}(n)$的！因此，我们如果要将$Z_i$替换成别的东西，那应该是一个比$n$的一次方更低阶的函数，甚至是一个常数。

现在回看GAU，它的激活函数换成了$\text{relu}^2(\cdot)$时，其Attention情况是类似的，甚至会更稀疏。这是因为$\text{relu}$操作有直接置零的作用，不像$\exp(\cdot)$总是正的，同时GAU“标配”旋转位置编码RoPE，在《Transformer升级之路：2、博采众长的旋转式位置编码》中我们就推导过，RoPE本身自带一定的远程衰减的能力。综合这些条件，GAU的归一化因子也应该是低于$\mathcal{O}(n)$的阶甚至是常数级别的。

熵不变性 #

由此，我们可以总结出GAU的三个解决方案，一是预训练和微调都用同一个固定的$n$；二是依然使用动态的样本长度$n$，但是预训练时需要用不同长度的样本来混合训练，不能只使用单一长度的样本；三就是像Softmax那样补充上一个归一化因子，让模型自己去学：
\begin{equation}a_{i,j} = \frac{1}{Z_i}\text{relu}^2\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right),\quad Z_i = \sum_{i=1}^n \text{relu}^2\left(\frac{\boldsymbol{q}_i\cdot\boldsymbol{k}_j}{\sqrt{d}}\right)\end{equation}

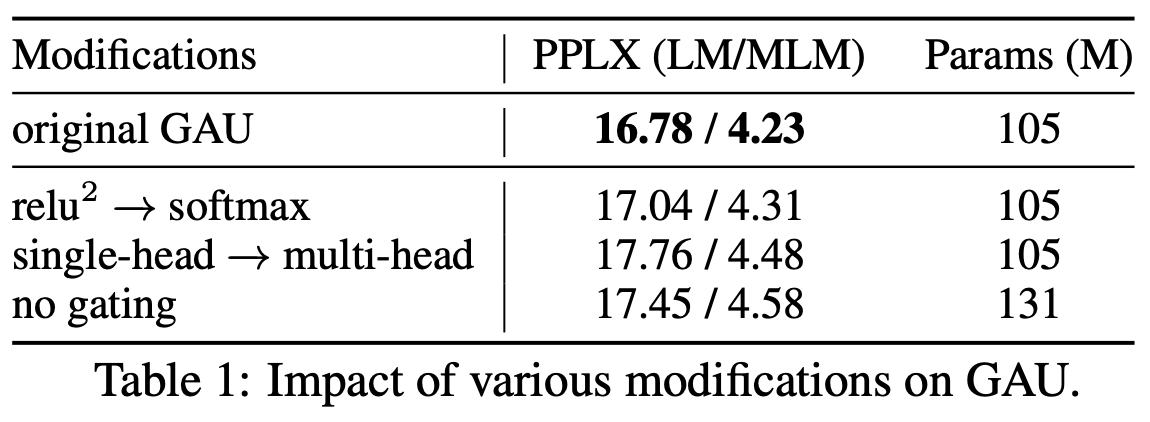
既然存在这些解决方案，那为什么我们还说“Attention与Softmax更配”呢？GAU的$\text{relu}^2(\cdot)$哪里不够配呢？首先，我们看GAU原论文的消融实验，显示出$\text{relu}^2(\cdot)$换成Softmax，效果基本是一致的：

GAU的squared_relu换成softmax效果是相近的

GAU的squared_relu换成softmax效果是相近的

有了这个基本保证之后，我们就可以看Softmax比$\text{relu}^2(\cdot)$好在哪里了。我们看刚才提到的GAU三个解决方案，方案一总让人感觉不够自适应，方案二必须用多种长度训练显得不够优雅，至于方案三补充了归一化因子后形式上相比Softmax反而显得“臃肿”了。所以，总体来说还是用Softmax显得更为优雅有效。

此外，泛化能力可以简单分为“内插”和“外推”两种，在这里内插（外推）指的是测试长度小于（大于）训练长度。我们刚才说归一化因子是常数量级，更多是在内插范围内说的。对于外推来说，如果长度足够长，$\boldsymbol{q}_i,\boldsymbol{k}_j$都“挤”在一起，所以很难保持距离超过某个范围就很接近于0的特性。而如果我们用Softmax的话，就是它可以推导出一个“熵不变性”的版本，来增强模型的外推能力：
\begin{equation}Attention(Q,K,V) = softmax\left(\frac{\log_{512} n}{\sqrt{d}}QK^{\top}\right)V\end{equation}
在《从熵不变性看Attention的Scale操作》中我们做过简单的对比实验，显示该版本确实能提高模型在超出训练长度外的效果。

那么，$\text{relu}^2(\cdot)$能否推一个“熵不变性”的版本呢？答案是不能，因为它相当于是通过温度参数来调节分布的熵，这要求激活函数不能是具备正齐次性，比如对于幂函数有$(\lambda \boldsymbol{q}_i\cdot\boldsymbol{k}_j)^n=\lambda^n (\boldsymbol{q}_i\cdot\boldsymbol{k}_j)^n$，归一化后$\lambda^n$就抵消了，不起作用。激活函数最好比幂函数高一阶，才比较好实现这个调控，而比幂函数高阶的函数，最常见就是指数函数了，而指数归一化正好就是Softmax。

本文小结 #

本文分析了GAU在微调效果不佳的原因，发现Attention的归一化因子应该是接近常数量级的，所以GAU用$n$或者$n^2$做归一化因子会表现不佳。总的来说，笔者认为Attention还是跟Softmax更配，它是一个不错的基准，并且还可以通过“熵不变性”的拓展来进一步增强外推能力。

转载到请包括本文地址：https://spaces.ac.cn/archives/9019

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (Apr. 07, 2022). 《听说Attention与Softmax更配哦～ 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/9019

@online{kexuefm-9019,
        title={听说Attention与Softmax更配哦～},
        author={苏剑林},
        year={2022},
        month={Apr},
        url={\url{https://spaces.ac.cn/archives/9019}},
}