三连杆装置曲线方程

本创意装置来自牧夫天文论坛的zhangyf1997同好。

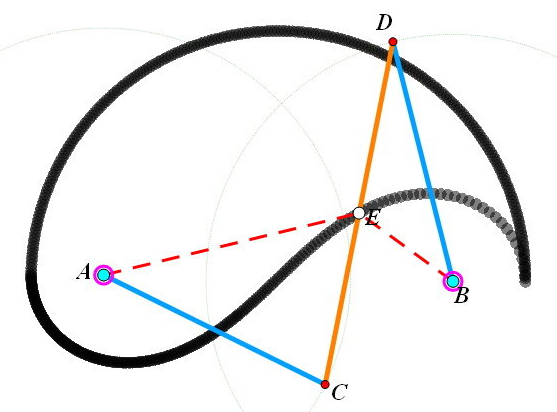
结构：
1、A、B为两定点，可看作有刚性杆连接；
2、AC为动力杆，绕点A转动；
3、BD为从动杆，CD为连杆。

长度数据：
1、CD=AB=$\sqrt{2}$；
2、AC=BD=1。
3、E是CD中点

求：E点的轨迹方程（即图中黑色那条，很有趣吧？）

为了求出本题的曲线方程，BoJone依旧采用向量的方法，但是这一次有点特殊，采用“质点法”记号。在《绕来绕去的向量法》中，BoJone学到了一个称之为“质点法”的东西，当然也不是什么神秘的新的东西，在我看来，它就是一种向量法的简便记号，即把向量$\vec{AB}$写成$B-A$（两个点相减），并且定义$AB$就是两个向量的点积$\vec{OA}\cdot \vec{OB}$，其余都没有太大变化。只要在运算过程中记住：1、注意要使用明显的符号把“点”与“数”区分开来，不至于混淆；2、向量没有除法，不能随便在等式两边随便约去一些向量。

言归正传，在本题中，以A为原点，AB为x轴建立坐标系，可以写出：
$$\begin{aligned}B=(\sqrt{2},0) \\ 2E=C+D\end{aligned}\tag{1}$$$$1=C^2=(D-B)^2=D^2+B^2-2DB\tag{2}$$$$2=B^2=(D-C)^2=D^2+C^2-2DC\tag{3}$$
由(1)得$C=2E-D$，两端平方得
$$1=4E^2+D^2-4DE\tag{4}$$
将$C=2E-D$代入(3)得$$1=D^2-2D(2E-D)=3D^2-4ED\tag{5}$$
联合(4)(5)得到$2E^2=D^2$，将其代入(5)得到$1=6E^2-4ED$，代入(2)得$2DB=1+2E^2$。至此，向量的工作完成了，接下来我们只有回到坐标系了（向量已经帮助我们将问题化简成一元一次方程组了）。设$E=(x,y),D=(D_1,D_2)$，那么有
$$\begin{aligned}6(x^2+y^2)-1=4D_1 x+4D_2 y \\ 1+2(x^2+y^2)=2\sqrt{2} D_1\end{aligned}$$

解得到$D_1=\frac{1+2(x^2+y^2)}{2\sqrt{2}},D_2=\frac{6(x^2+y^2)-1-4D_1 x}{4y}$

由$2E^2=D^2$得$2(x^2+y^2)=D_1^2+D_2^2$，将上面解得的$D_1,D_2$代入后化简即得轨迹方程，这是一个极度复杂的过程..

$$2(x^2+y^2)=(\frac{1+2(x^2+y^2)}{2\sqrt{2}})^2+(\frac{6(x^2+y^2)-1-4(\frac{1+2(x^2+y^2)}{2\sqrt{2}}) x}{4y})^2$$

一个比较“简单”的展开结果为：
$$\begin{aligned}8 x^6-24 \sqrt{2} x^5+24 x^4 y^2+44 x^4-48 \sqrt{2} x^3 y^2-8 \sqrt{2} x^3+24 x^2 y^4+56 x^2 y^2-10 x^2-24 \sqrt{2} x y^4-8 \sqrt{2} x y^2 \\ +2 \sqrt{2} x+8 y^6+12 y^4-10 y^2+1=0\end{aligned}$$

想不到居然是一个六次曲线！不过，还可以稍稍化简一些，这个曲线由两部分组成：
$$\begin{aligned}2y^2 +2 x^2= 2 \sqrt(2) x+1 \\ 4(y^2+x^2+1-\sqrt{2} x)^2=8 x^2-8 \sqrt{2} x+5\end{aligned}$$

由于运算过程实在太过复杂，就连我这个很喜欢手算的人也不想算下去，因此，这些结果都是wolframalpha完成的。

有读者能够提供更简单的方法的话，欢迎告知BoJone。

转载到请包括本文地址：https://spaces.ac.cn/archives/1168

更详细的转载事宜请参考：《科学空间FAQ》