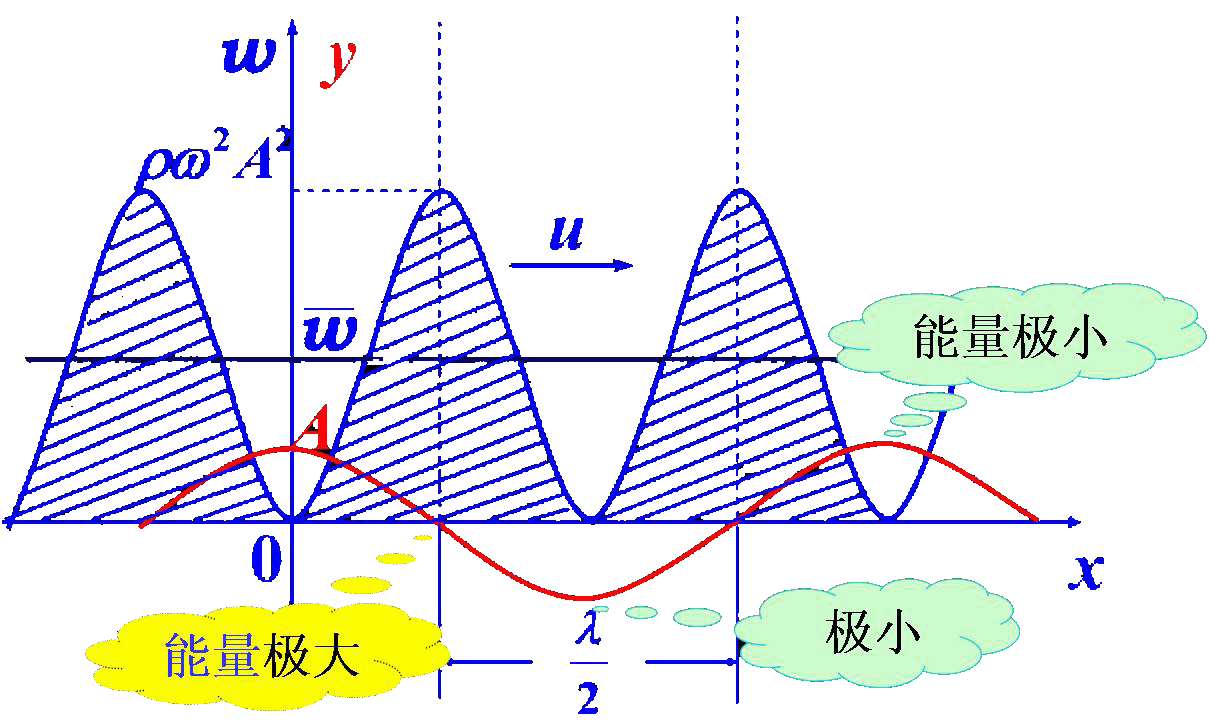
当弹性波传播到介质中的某处时,该处原来不动的质点开始振动,因而具有动能,同时该处的介质也将产生形变,因而也具有
以弹性棒中的简谐横波为例来分析:
有一行波:

质元的速度:
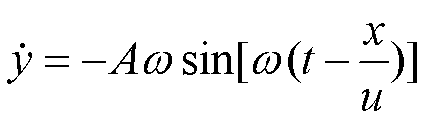
质量为Δm的媒质其动能为:
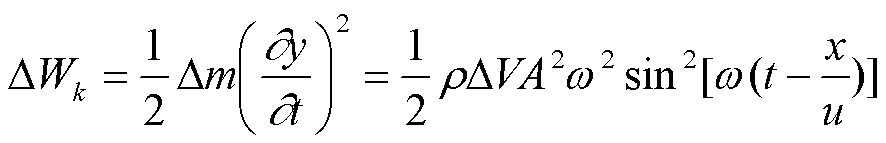
单位体积媒质中弹性势能等于弹性模量与应变平方乘积的一半。
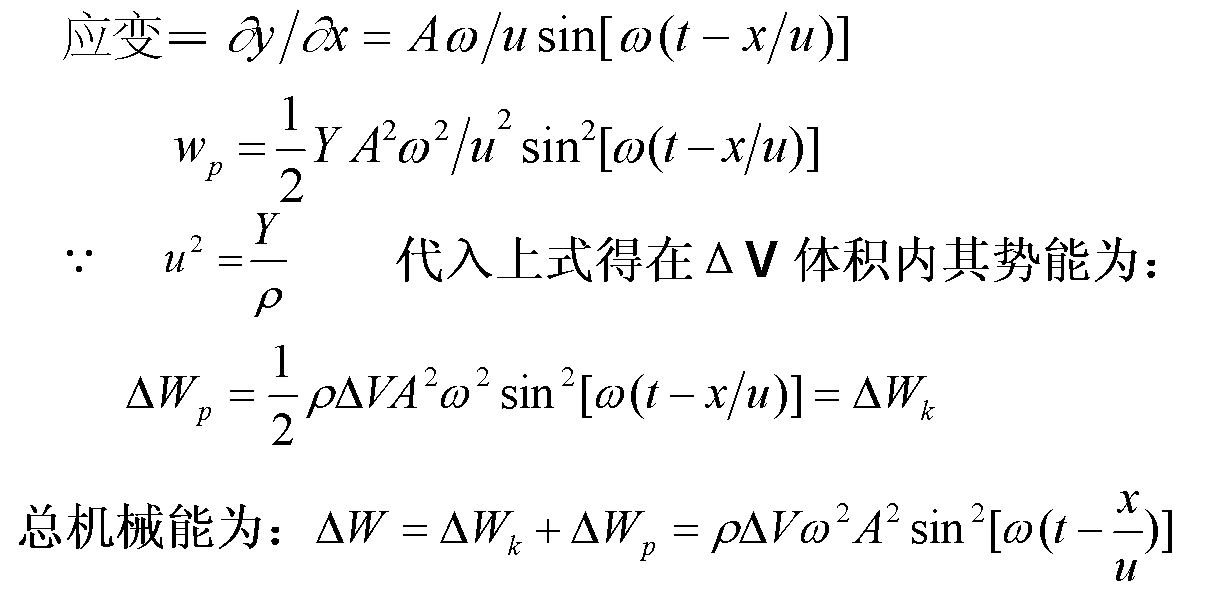
振动系统:
![]()
系统与外界无能量交换。
波动质元:
![]()
每个质元都与周围媒质交换能量。

波动能量的推导
能流P—单位时间内垂直通过某一截面的能量称为波通过该截面的能流,或叫能通量。
设波速为 u,在Δt时间内通过垂直于波速截面ΔS的能量:
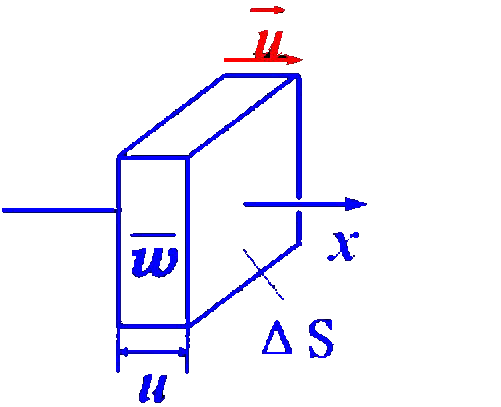
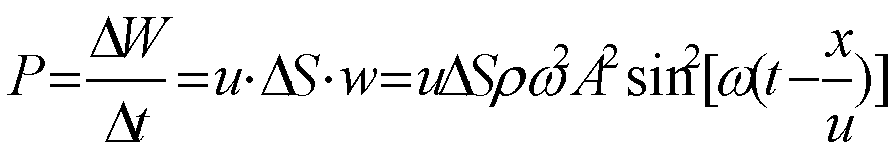
能流随时间周期性变化,总为正值
在一个周期内能流的平均值称为平均能流
![]()
波的强度
通过垂直于波动传播方向的单位面积的平均能流称为平均能流密度,通常称为能流密度或波的强度。
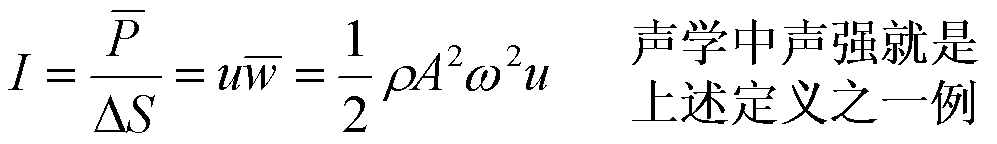
能流密度是单位时间内通过垂直于波速方向的单位截面的平均能量。
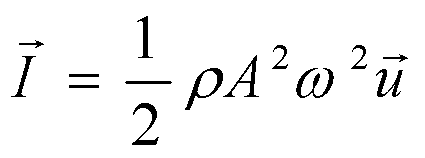
能流密度是矢量,其方向与波速方向相同
波通过媒质时,一部分能量要被媒质吸收。
造成吸收的因素:
①内摩擦: 机械能→热运动能(不可逆);
②热传导: 疏部、密部有温差,发生热交换, 机械能→热运动能 (不可逆);
③分子碰撞: 非弹性碰撞使分子规则振动能→分子内部无规则的转、振能(不可逆)。
波的吸收
对平面波:
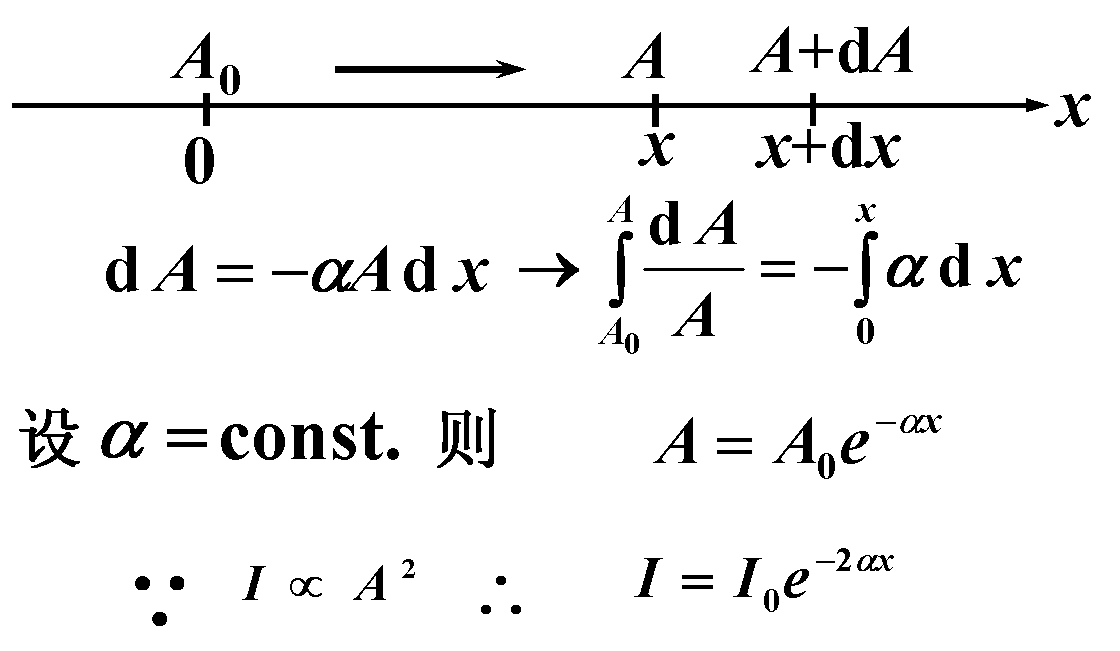
α 称为媒质的吸收系数
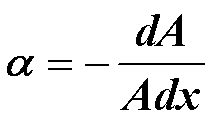
与媒质的性质有关;与波的频率有关。
在钢中α= 2/m,
前进1.15m 强度衰减为百分之一。
在空气中α= 500/m,
前进4.6mm 强度衰减为百分之一。
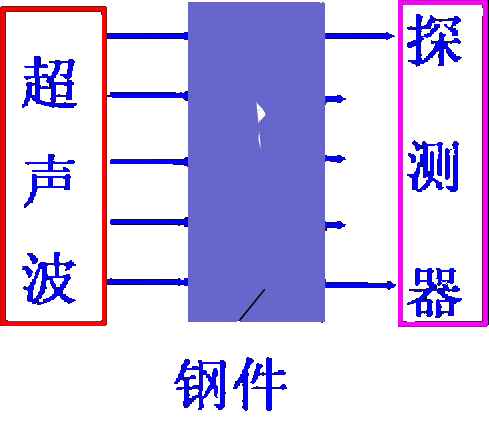
ω↑则α↑ 空气中低频波可传得很远。
(广场上有乐队,你在远处只听到大鼓声)