前进中的波动，称为行波。

描述介质中各质点的位移随时间变化的数学函数式称为行波的波动表式(或波动方程)。

设坐标原点的振动为：

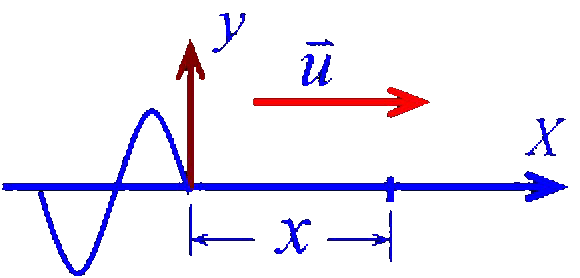
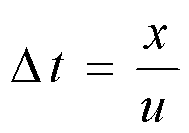
相位落后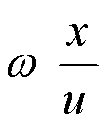

所以 p点的运动方程：

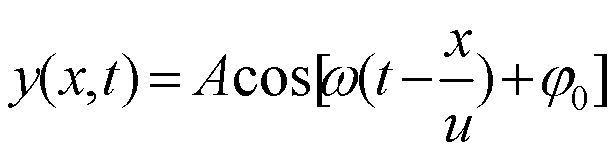
因此下述表达式等价：

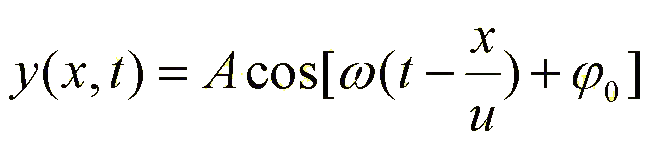
将平面波的波函数对空间和时间求导，可得

若y₁，y₂分别是它的解，则 （y₁＋y₂）也是它的解，即上述波动方程遵从叠加原理。

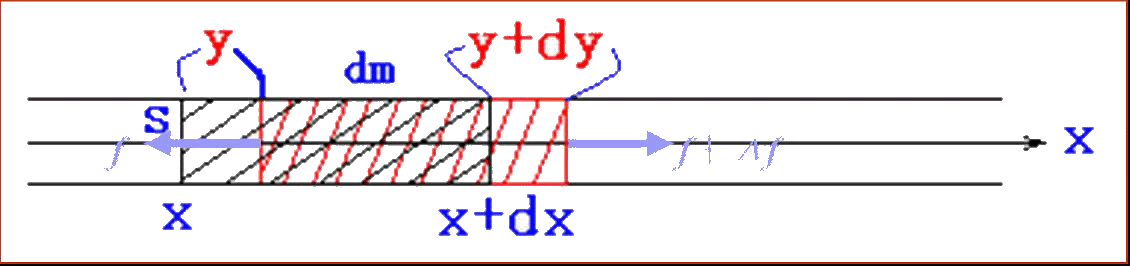
取棒中任一小质元原长dx，质量为 dm=ρSdx

受其它部分的弹性力为f和f+df

质元的运动学方程为：

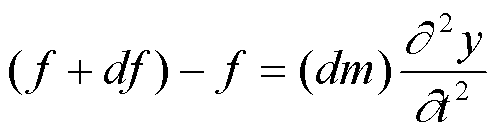
根据弹性模量的定义：

波动方程的推导

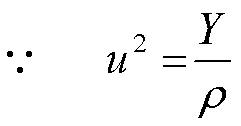
代入运动方程得

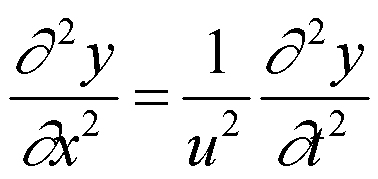
结论：任何物理量只要满足上述方程，则它一定按波的形式传播。而且对时间偏导数系数的倒数就是波速的平方。