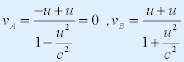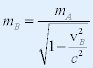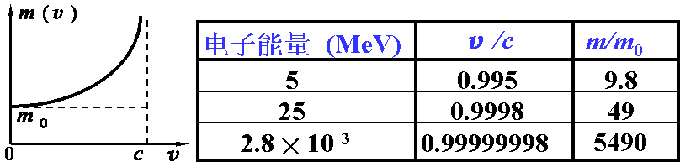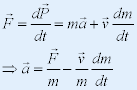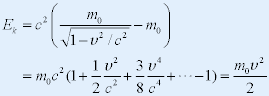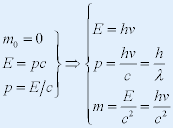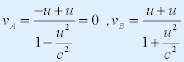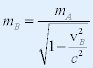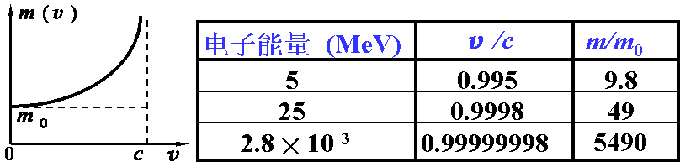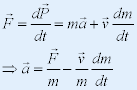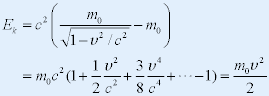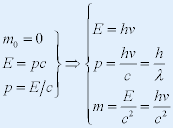| 【上一页】【下一页】【返回目录】 |
| §5.4 狭义相对论动力学基础 |
| 由爱因斯坦相对性原理,物理规律在一切的惯性系中有相同的形式。另外,物理学中的基本守恒定律,如: |
| 质量守恒定律、动量守恒定律和能量守恒定律,是普适成立的。相对论动力学就是在这些基础上建立起来的。 |
| 1. 相对论质量(relativistic mass) |
| 在牛顿第二定律中: |
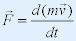 |
| 若m为常量,将与相对论矛盾: |
| ⅰ° 导致超光速; |
| ⅱ°对洛仑兹变换,不满足相对性原理。 |
| 修正原则: |
ⅰ° 使动力学方程满足洛仑兹变换下的不变性;  相对论动力学形式不变 相对论动力学形式不变 |
| ⅱ°在v << c时能过渡到牛顿力学。 |
| 为使动量守恒对洛仑兹变换保持不变,必须认为m = m(v),下面由动量守恒导出m与v的关系: |
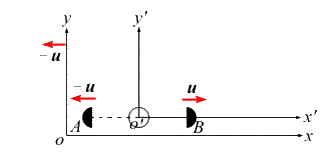 |
| (图一) |
| 设一粒子在S'中静止,后分裂为相同的两块 A、B,分别沿+X'和-X'方向运动。 |
| S 系中: |
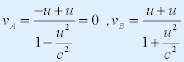 |
| 由质量守恒和动量守恒有: |
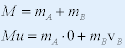 |
| 由上面三个式子得: |
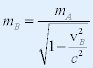 |
| 令 mA = m0 叫作 静止质量(rest mass) |
| 再令 mB = m,vB= v,则: |
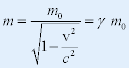 |
| --质速公式 (揭示了物质与运动的不可分割性) |
| m 称为相对论质量(relativistic mass)。 |
| 例如:电子的运动质量 |
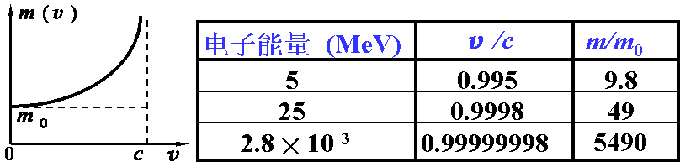 |
| (图二) |
| 考夫曼(K.Kaufmann)利用不同速度的电子在磁场中的偏转角来测定电子的质量, 证明了质速公式的正确性. |
| 意义: |
| ⅰ° 当速度足够高时(> 0.5C),物质的质量增加才明显(0.5C增大15%) |
ⅱ°对当速度足够接近C时,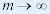 ,也就是说,V越大,则m越大,也就越难加速。因此,速度以光速为极限。 ,也就是说,V越大,则m越大,也就越难加速。因此,速度以光速为极限。 |
| ⅲ° 某些基本粒子,如光子、中微子等,其传播速度是C,因此,它们没有静止质量。 |
| 2. 狭义相对论运动方程 |
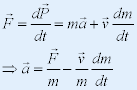 |
| 由: |
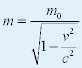 |
| 得: |
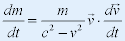 |
| 两式联立得: |
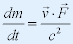 |
 |
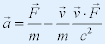 |
| --加速度方向与外力方向不一致! |
| 3. 质能关系 |
| 质量守恒和能量守恒是自然界的普适规律,根据相对论原理能得到关于质量和能量的关系。 |
| ⅰ°物体的动能 |
| 经典力学 相对论力学 |
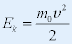  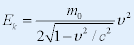 ? ? |
| 在相对论中,认为动能定理仍适用。若取质点速率为零时动能为零。则质点动能就是其从静止到以v 的速率运动的过程中,合外 |
| 力所做的功. |
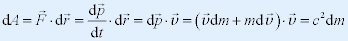 |
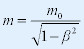 |
两边微分 |
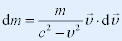 |
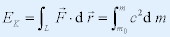 |
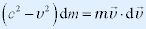 |
 |
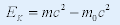 |
| --相对论的动能表达式 |
| 讨论: |
| (1) 注意相对论动能与经典力学动能的区别和联系 |
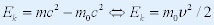 |
当V<< C 时,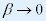 , 有: , 有: |
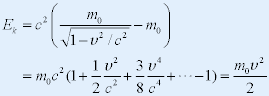 |
| V<< C 时,出现退化,牛顿力学中的动能公式 |
(2) 当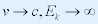 ,意味着将一个静止质量不为零的粒子,使其速度达到光速,是不可能的。 ,意味着将一个静止质量不为零的粒子,使其速度达到光速,是不可能的。 |
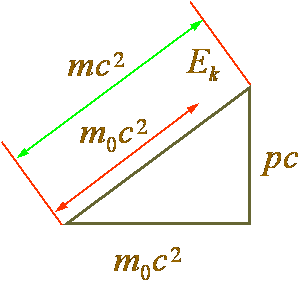
| ⅱ°静止能量总能量 |
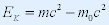 |
| 静止能量(任何宏观静止物体具有能量): |
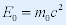 |
| 总 能 量(相对论质量是能量的量度): |
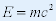 |
| ⅲ°质能关系 |
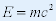  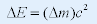 |
| 物体的相对论总能量与物体的总质量成正比 ——质量与能量不可分割,质量守恒就意味着能量守恒。物质 |
| 的质量是能量的一种表现形式。 |
| 静止物体本身蕴藏着巨大的能量! |
| 例如 1kg 水由 0 度加热到 100 度,所增加的能量为: |
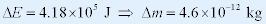 |
| 对于一个存在有内部结构和内部运动的系统来说: |
 |
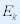 |
| -- 系统随质心平动的动能 |
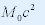 |
| -- 系统的内能 |
| 4. 相对论能量和动量的关系 |
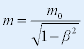 |
| 两边平方有: |
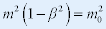 |
| 两边乘以C4有: |
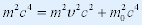 |
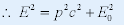 |
| 反映了能量与动量的不可分割性与统一性. |
| 取极限情况考虑,如光子 |
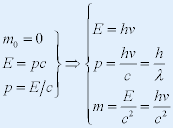 |
 |
| (图三) |
| [例5--6] 已知质子和中子的质量分别为: |
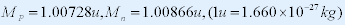 |
两个质子和两个中子形成一个氦核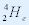 ,实验测得它的质量MA=4.00150u,试计算形成一个氦核时所放出的能量 ,实验测得它的质量MA=4.00150u,试计算形成一个氦核时所放出的能量 |
| --原子核的结合能。 |
| [解]: |
| 质子和中子组成氦核之前,总质量为: |
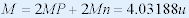 |
| 而实验测出氦核的质量 MA < M , |
| 质量亏损 : |
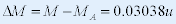 |
| 由质能公式可得: |
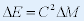 |
| 说明质子和中子组成原子核时,将有大量能量放出. |
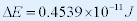 |
| 结合成1mol的氦核(4.002g)时,放出的能量为: |
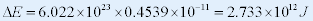 |
| 相当于燃烧100吨煤所放出的热量。 |
| |
|