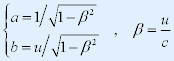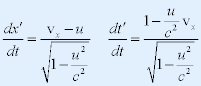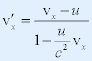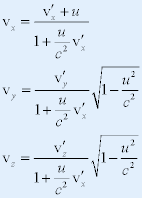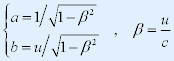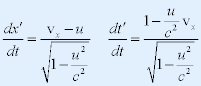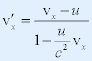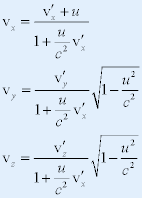| 【上一页】【下一页】【返回目录】 |
| §5.3 洛伦兹变换(Lorentz transformation) |
| 荷兰物理学家洛仑兹为挽救以太,1904年建立了以静止的以太坐标系到其它惯性系的变换式,即著名的洛仑兹变换式,不过他并没有 |
| 意识到这个变换式的深刻意义。1905年爱因斯坦从新时空观也得到同样的变换方程。 |
| 1、时空变换 |
如图一,t'=t=0,设时,O'O重合,S相对S'以 运动。 运动。 事件在S系描述P(X,Y,Z),在S'描述P(X',Y',Z')。 事件在S系描述P(X,Y,Z),在S'描述P(X',Y',Z')。 |
| 由于
在Y,Z方向无运动,则:Y=Y',Z=Z' |
| 因而只要讨论(X,t)和(X',t')关系。 |
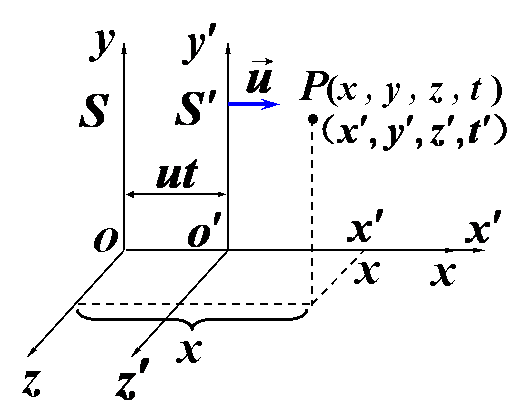 |
| (图一) |
| 讨论: |
| ⅰ°由于相对性原理,变换应该是线性的。因为在一个惯性系作惯性运动而在另一个惯性系作曲线运动是不可能的。 |
| ⅱ°它应该满足光速不变原理。 |
| ⅲ°其结果应当满足当 v << c 时,等效于伽利略变换。 |
| 可能的数学变换形式: |
 |
| 式中a,b待求,但与v有关。 |
先考虑 点相对于S系的运动:这时有 点相对于S系的运动:这时有 ,则: ,则: |
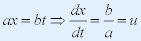 (1) (1) |
再考虑光速不变,则在 点和 点和 点发出的光束有: 点发出的光束有: |
 (2) (2) |
| (1)(2)式联立可得: |
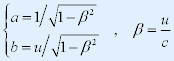 |
| 因此有洛仑兹变换为: |
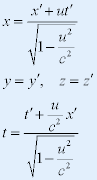  |
L-变换是相对论时空观的具体体现。当v<<c时,L-变换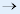 G-变换。 G-变换。 |
| 2、同时的相对性之定量解释 |
| 对于车厢系,光到达A、 B点的时间相同,即: |
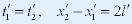 |
| 那么,对于地面系,由洛伦兹变换: |
 |
| 即有: |
 |
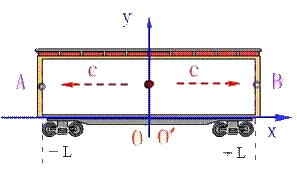 |
| (图二) |
| 3、收缩因子 |
| 根据收缩因子,有 v < c,否则无意义。所以相对论认为,任何物体的速度不能超过真空中的光速。 |
| (c + v)的出现是指光对运动点的速度,又称几何速度<2c |
| 4、速度变换 |
| 由洛仑兹坐标变换 |
 |
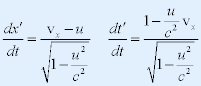 |
 |
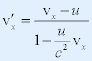 |
| 由洛仑兹变换 |
 |
 |
| 由上面两式得 |
 |
 |
| 同样得 |
 |
 |
| 洛仑兹速度变换式 |
| 正变换 |
 |
| 逆变换 |
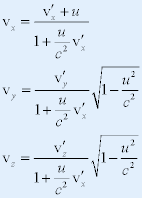 |
| [例5-1] 在地面上测有两个飞船A、B分别以+0.6c和-0.6C沿相反方向飞行,如图三所示.求飞船B相对于飞船A的速度为多少? |
 |
| (图三) |
| [解]: |
| 以地面为参考系K,将K'系固定在飞船A上.B相对于A的速度为:(即相对K'系的速度) |
 |
| 若按伽利略速度变换,其结果为: |
 |
| 显然是不合理的。 |
| |
| [例5--2]两只飞船,彼此以 0.98c的相对速率朝相反的方向飞过对方,宇宙飞船Ⅰ中的观察者测得另一只宇宙飞船 Ⅱ的长度为自己 |
| 飞船的2/5,求:飞船Ⅱ的相对静止长度与飞船Ⅰ的相对静长度之比是多少? |
| [解]: |
| 设飞船Ⅰ为K系, 飞船Ⅱ为K'系. |
| K系测得飞船Ⅱ的长度为: |
 |
| 按题意: |
 |
| 故它们的相对静长之比为: |
 |
| |
| [例5--3]有一根刚性米尺静止于K'系中,且与O'X'轴成45°角,K'系相对于K系沿X轴正方向以0.8c的速度匀速运动,则在K系中观测 |
| 该尺的长度及与OX轴的夹角是多少? |
| [解]: |
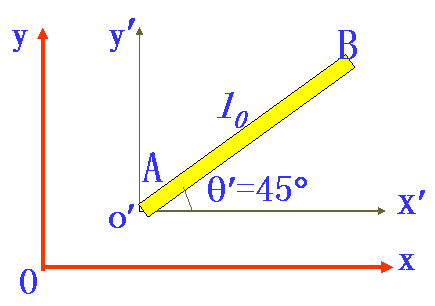 |
| (图四) |
| 在K系中,棒长为: |
 |
设棒长与X轴的夹角为 : : |
 |
| 可见: |
 |
 |
| (图五) |
[例5—4]  介子固有寿命的实验值为(2.603±0.002)×10-8S.现代物理实验测出以0.91C高速飞行的 介子固有寿命的实验值为(2.603±0.002)×10-8S.现代物理实验测出以0.91C高速飞行的 介子的平均飞行距离 介子的平均飞行距离 |
| 为17.135m,试分析这个结果. |
| [解]: |
由平均飞行距离可推算出在实验室系中的 介子的平均寿命为: 介子的平均寿命为: |
 |
按相对论效应,可算出 介子的固有寿命的理论值为: 介子的固有寿命的理论值为: |
 |
| 理论值与实验值只相差0.001×10-8s,这说明相对论的时间膨胀预言是正确的. |
| |
|