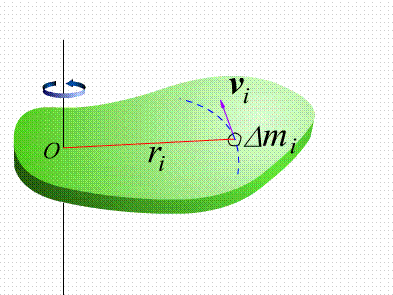
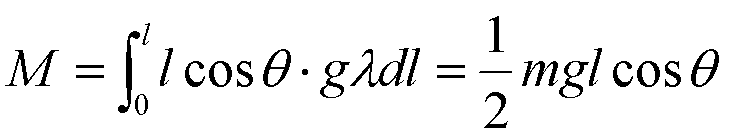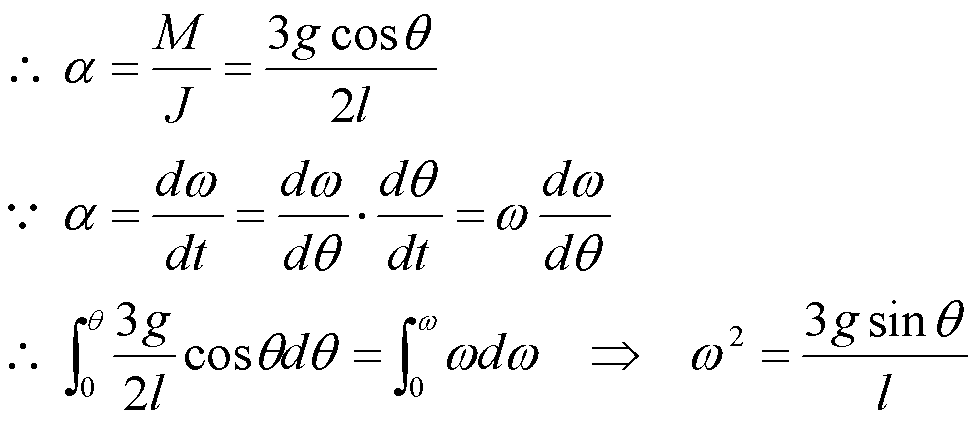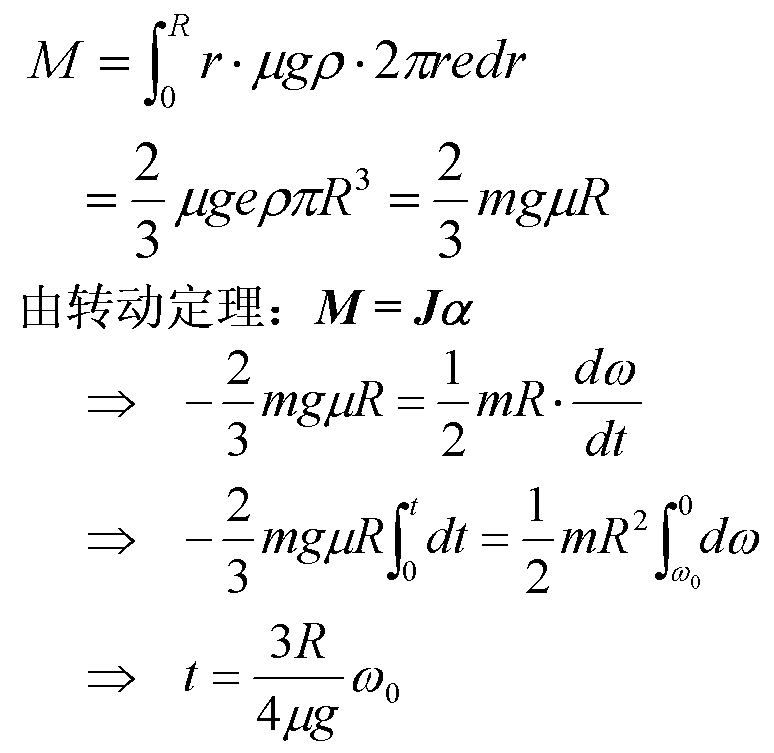设刚体绕oz轴以角速度ω转动,把刚体看作n个质元构 成的质点系每个质元质量为△mi,所以总动能:
![]()
![]() ——称为刚体对转轴的转动惯量
——称为刚体对转轴的转动惯量
刚体转动动能的一般表达式:
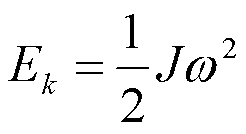
对于连续分布的刚体:
![]()
刚体的转动惯量J对应于质点的m。m是质点惯性的量,m越大,运动状态就越不易改变。同样地,对于刚体,J越大,其转动状态就
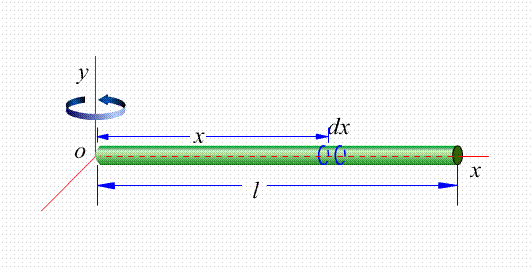
【解】取如图坐标,dm=λdx,对中点
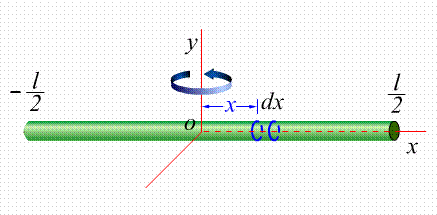
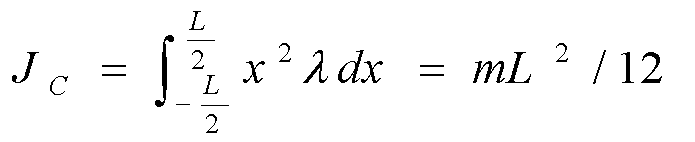
对端点:
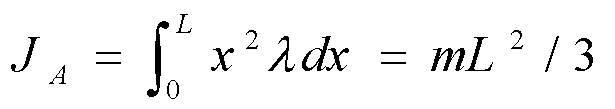
几种物体的转动惯量
 |
|
 |
|
 |
|
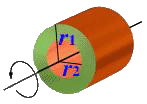 |
|
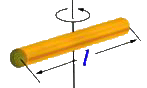 |
|
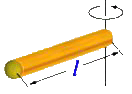 |
|
 |
|
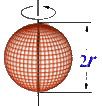 |
|
ⅰ 刚体的转动惯量与刚体的质量、质量的分布以及转轴的位置均有关系。
ⅱ 转动惯量的国际单位是kg•m2
ⅲ 平行轴定理
设刚体绕过质心C的转轴的转动惯量为 JC ,将转轴朝任一方向平移一个距离
![]()
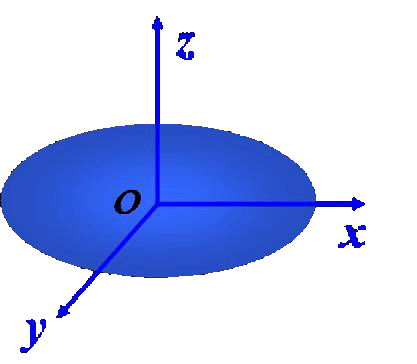
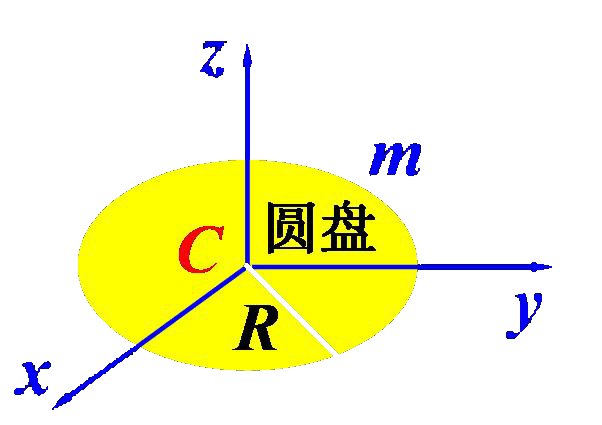
ⅳ 对薄平板刚体的正交轴定理
设刚性薄板平面为xy面,z轴与之垂直,则任何过原点o,绕三个轴的转动惯
![]()
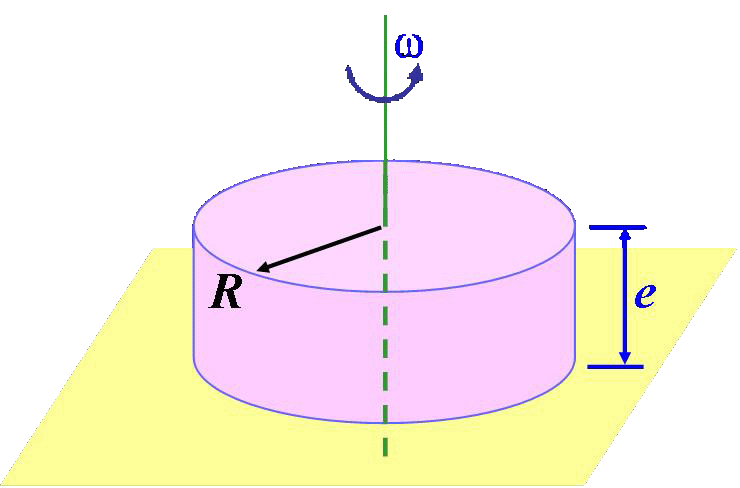
【解】已知圆盘
![]()
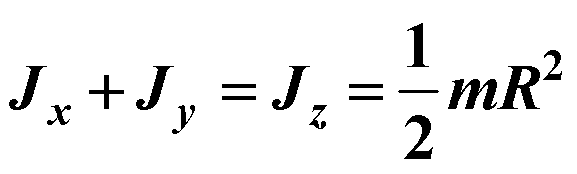
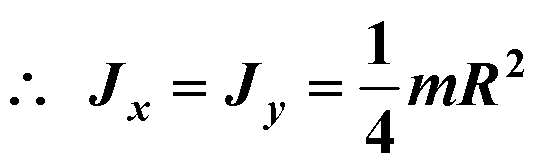
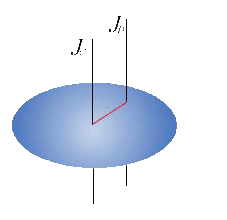
思考:下图中Jz的如何求
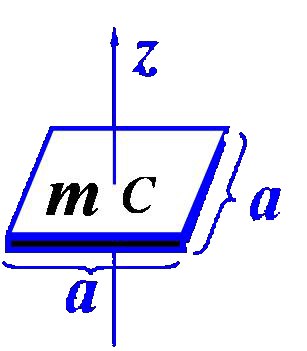 |
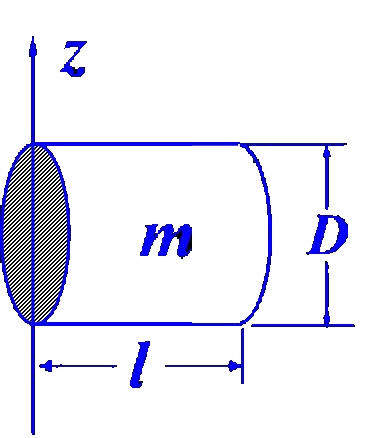 |
在质点动力学中,只要质点受外力作用,并有位移,则力将对质点作功;同样地,当刚体在外力矩的作用下绕定轴转动而发生角位
讨论:如图的情况
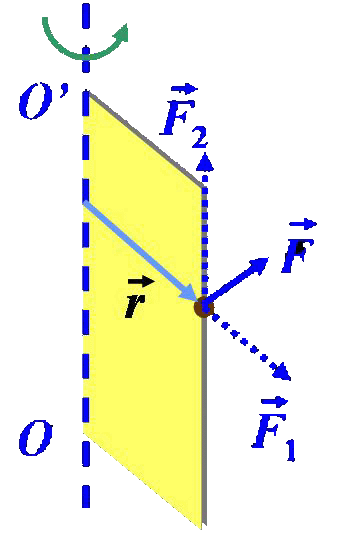
若F1//r,则M = 0;无转动。
若F2//OO’,则M⊥ OO’;无转动。
若F⊥r,则M // OO’;有转动。
可见,定轴转动中,只有转轴方向的力矩分量才对作功有贡献。因此,这时
如图,力 Fi 所作的元功:
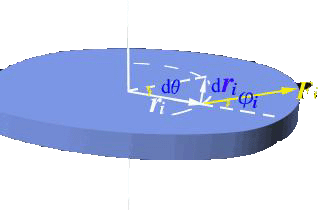
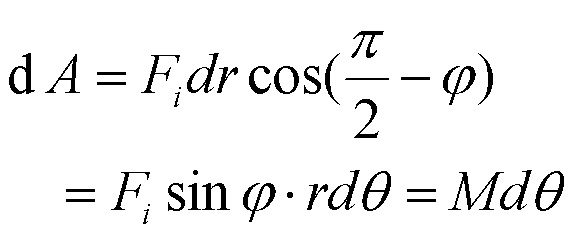
合外力矩的总功:
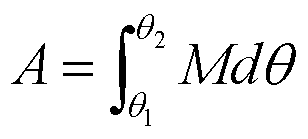
![]()
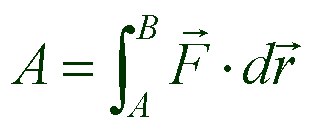
从上式看到:外力对刚体所作的功等于合力矩对角位移的积分,它是力做的功在刚体转动中的特殊表现形式。
注意:力矩是矢量。在定轴转动问题中,只有轴向力矩分量才对作功有贡献,应记为Mz,它是标量。简记为M,下同。
质点系的功能原理当然地适用于定轴转动的刚体。而且,当刚体定轴转动时,刚体的机械能表现为动能。即有:
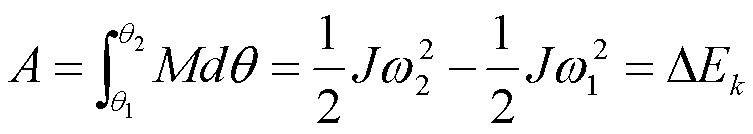
总外力矩对刚体所作的功等于刚体转动动能的增量。叫做刚体定轴转动的动能定理。
力矩是引起刚体转动状态变化的原因,定量的描述如下:
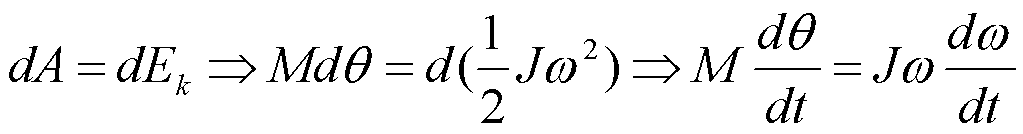
![]() ——与牛顿第二定律的数学形式相似
——与牛顿第二定律的数学形式相似
【解】如图选择坐标系。杆的下拜只能作刚体处理,设质量微元dm,
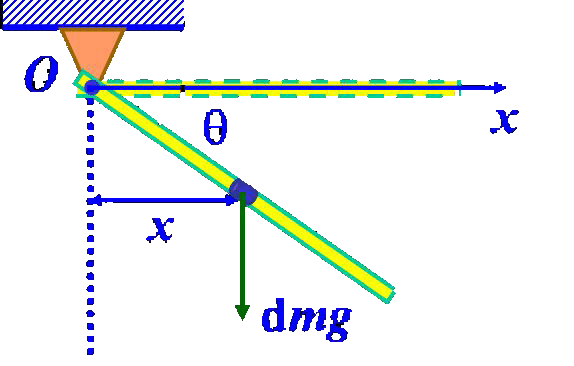
dM = xgdm
设质量线密度为λ,则:x =lcosθ,dm=λdl,因此,