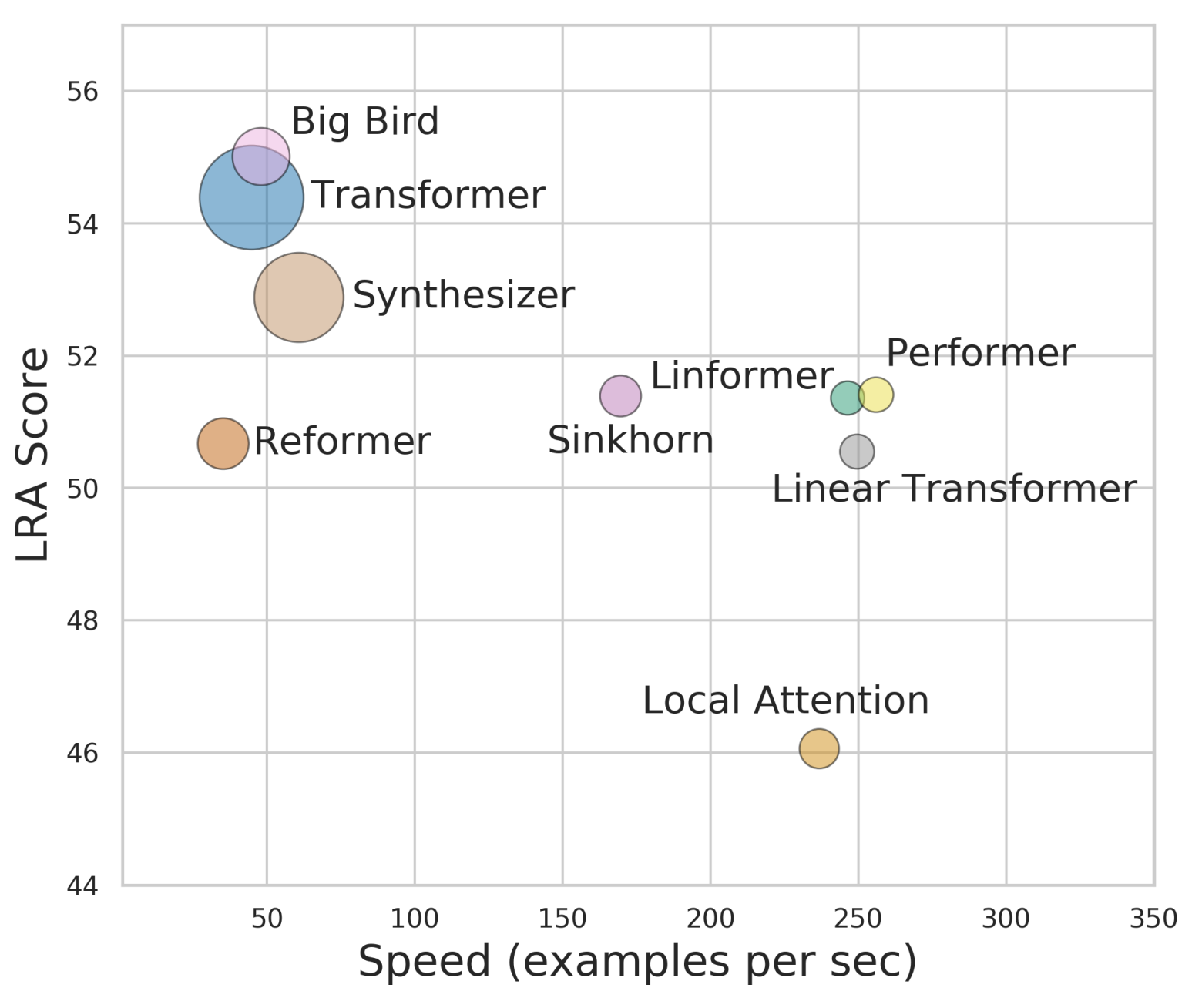
Performer:用随机投影将Attention的复杂度线性化
By 苏剑林 | 2020-12-01 | 81070位读者 | 引用Attention机制的$\mathcal{O}(n^2)$复杂度是一个老大难问题了,改变这一复杂度的思路主要有两种:一是走稀疏化的思路,比如我们以往介绍过的Sparse Attention以及Google前几个月搞出来的Big Bird,等等;二是走线性化的思路,这部分工作我们之前总结在《线性Attention的探索:Attention必须有个Softmax吗?》中,读者可以翻看一下。本文则介绍一项新的改进工作Performer,出自Google的文章《Rethinking Attention with Performers》,它的目标相当霸气:通过随机投影,在不损失精度的情况下,将Attention的复杂度线性化。
说直接点,就是理想情况下我们可以不用重新训练模型,输出结果也不会有明显变化,但是复杂度降到了$\mathcal{O}(n)$!看起来真的是“天上掉馅饼”般的改进了,真的有这么美好吗?
层次分解位置编码,让BERT可以处理超长文本
By 苏剑林 | 2020-12-04 | 118305位读者 | 引用大家都知道,目前的主流的BERT模型最多能处理512个token的文本。导致这一瓶颈的根本原因是BERT使用了从随机初始化训练出来的绝对位置编码,一般的最大位置设为了512,因此顶多只能处理512个token,多出来的部分就没有位置编码可用了。当然,还有一个重要的原因是Attention的$\mathcal{O}(n^2)$复杂度,导致长序列时显存用量大大增加,一般显卡也finetune不了。
本文主要面向前一个原因,即假设有足够多的显存前提下,如何简单修改当前最大长度为512的BERT模型,使得它可以直接处理更长的文本,主要思路是层次分解已经训练好的绝对位置编码,使得它可以延拓到更长的位置。
从动力学角度看优化算法(七):SGD ≈ SVM?
By 苏剑林 | 2020-12-21 | 35705位读者 | 引用众所周知,在深度学习之前,机器学习是SVM(Support Vector Machine,支持向量机)的天下,曾经的它可谓红遍机器学习的大江南北,迷倒万千研究人员,直至今日,“手撕SVM”仍然是大厂流行的面试题之一。然而,时过境迁,当深度学习流行起来之后,第一个革的就是SVM的命,现在只有在某些特别追求效率的场景以及大厂的面试题里边,才能看到SVM的踪迹了。
峰回路转的是,最近Arxiv上的一篇论文《Every Model Learned by Gradient Descent Is Approximately a Kernel Machine》做了一个非常“霸气”的宣言:
任何由梯度下降算法学出来的模型,都是可以近似看成是一个SVM!
这结论真不可谓不“霸气”,因为它已经不只是针对深度学习了,而是只要你用梯度下降优化的,都不过是一个SVM(的近似)。笔者看了一下原论文的分析,感觉确实挺有意思也挺合理的,有助于加深我们对很多模型的理解,遂跟大家分享一下。
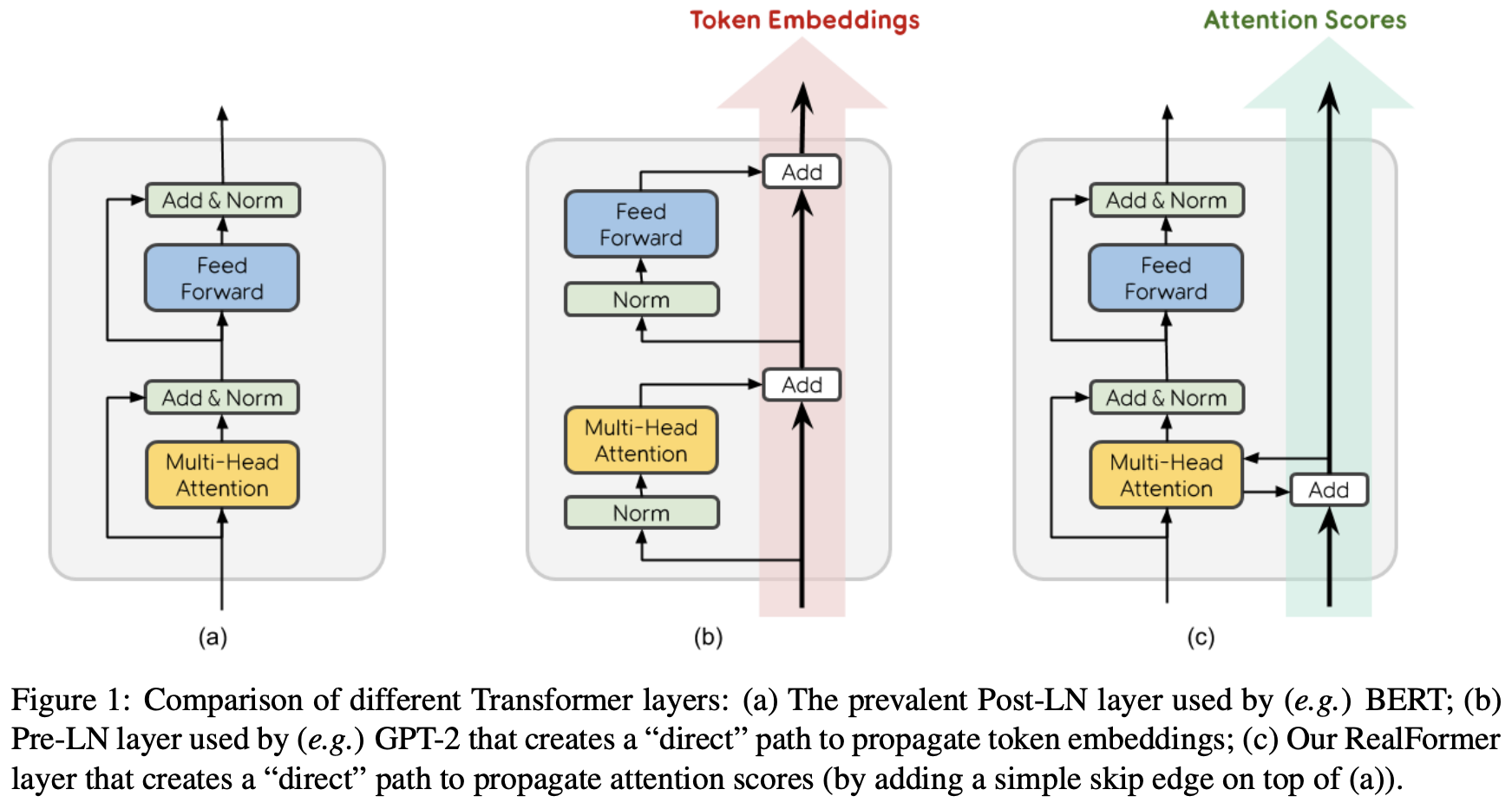
RealFormer:把残差转移到Attention矩阵上面去
By 苏剑林 | 2020-12-24 | 92242位读者 | 引用大家知道Layer Normalization是Transformer模型的重要组成之一,它的用法有PostLN和PreLN两种,论文《On Layer Normalization in the Transformer Architecture》中有对两者比较详细的分析。简单来说,就是PreLN对梯度下降更加友好,收敛更快,对训练时的超参数如学习率等更加鲁棒等,反正一切都好但就有一点硬伤:PreLN的性能似乎总略差于PostLN。最近Google的一篇论文《RealFormer: Transformer Likes Residual Attention》提出了RealFormer设计,成功地弥补了这个Gap,使得模型拥有PreLN一样的优化友好性,并且效果比PostLN还好,可谓“鱼与熊掌兼得”了。
两个多元正态分布的KL散度、巴氏距离和W距离
By 苏剑林 | 2021-07-08 | 101990位读者 | 引用正态分布是最常见的连续型概率分布之一。它是给定均值和协方差后的最大熵分布(参考《“熵”不起:从熵、最大熵原理到最大熵模型(二)》),也可以看作任意连续型分布的二阶近似,它的地位就相当于一般函数的线性近似。从这个角度来看,正态分布算得上是最简单的连续型分布了。也正因为简单,所以对于很多估计量来说,它都能写出解析解来。
本文主要来计算两个多元正态分布的几种度量,包括KL散度、巴氏距离和W距离,它们都有显式解析解。
正态分布
这里简单回顾一下正态分布的一些基础知识。注意,仅仅是回顾,这还不足以作为正态分布的入门教程。
概率密度
正态分布,也即高斯分布,是定义在$\mathbb{R}^n$上的连续型概率分布,其概率密度函数为
\begin{equation}p(\boldsymbol{x})=\frac{1}{\sqrt{(2\pi)^n \det(\boldsymbol{\Sigma})}}\exp\left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\top}\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\}\end{equation}
关于WhiteningBERT原创性的疑问和沟通
By 苏剑林 | 2021-10-09 | 65452位读者 | 引用在文章《你可能不需要BERT-flow:一个线性变换媲美BERT-flow》中,笔者受到BERT-flow的启发,提出了一种名为BERT-whitening的替代方案,它比BERT-flow更简单,但多数数据集下能取得相近甚至更好的效果,此外它还可以用于对句向量降维以提高检索速度。后来,笔者跟几位合作者一起补充了BERT-whitening的实验,并将其写成了英文论文《Whitening Sentence Representations for Better Semantics and Faster Retrieval》,在今年3月29日发布在Arxiv上。
然而,大约一周后,一篇名为《WhiteningBERT: An Easy Unsupervised Sentence Embedding Approach》的论文 (下面简称WhiteningBERT)出现在Arxiv上,内容跟BERT-whitening高度重合,有读者看到后向我反馈WhiteningBERT抄袭了BERT-whitening。本文跟关心此事的读者汇报一下跟WhiteningBERT的作者之间的沟通结果。
时间节点
首先,回顾一下BERT-whitening的相关时间节点,以帮助大家捋一下事情的发展顺序:
让人惊叹的Johnson-Lindenstrauss引理:应用篇
By 苏剑林 | 2021-09-24 | 35540位读者 | 引用上一篇文章中,我们比较详细地介绍了Johnson-Lindenstrauss引理(JL引理)的理论推导,这一篇我们来关注它的应用。
作为一个内容上本身就跟降维相关的结论,JL引理最基本的自然就是作为一个降维方法来用。但除了这个直接应用外,很多看似不相关的算法,比如局部敏感哈希(LSH)、随机SVD等,本质上也依赖于JL引理。此外,对于机器学习模型来说,JL引理通常还能为我们的维度选择提供一些理论解释。
降维的工具
JL引理提供了一个非常简单直接的“随机投影”降维思路:
给定$N$个向量$v_1,v_2,\cdots,v_N\in\mathbb{R}^m$,如果想要将它降到$n$维,那么只需要从$\mathcal{N}(0,1/n)$中采样一个$n\times m$矩阵$A$,然后$Av_1,Av_2,\cdots,Av_N$就是降维后的结果。
Transformer升级之路:1、Sinusoidal位置编码追根溯源
By 苏剑林 | 2021-03-08 | 129414位读者 | 引用最近笔者做了一些理解和改进Transformer的尝试,得到了一些似乎还有价值的经验和结论,遂开一个专题总结一下,命名为“Transformer升级之路”,既代表理解上的深入,也代表结果上的改进。
作为该专题的第一篇文章,笔者将会介绍自己对Google在《Attention is All You Need》中提出来的Sinusoidal位置编码
\begin{equation}\left\{\begin{aligned}&\boldsymbol{p}_{k,2i}=\sin\Big(k/10000^{2i/d}\Big)\\
&\boldsymbol{p}_{k, 2i+1}=\cos\Big(k/10000^{2i/d}\Big)
\end{aligned}\right.\label{eq:sin}\end{equation}
的新理解,其中$\boldsymbol{p}_{k,2i},\boldsymbol{p}_{k,2i+1}$分别是位置$k$的编码向量的第$2i,2i+1$个分量,$d$是向量维度。
作为位置编码的一个显式解,Google在原论文中对它的描述却寥寥无几,只是简单提及了它可以表达相对位置信息,后来知乎等平台上也出现了一些解读,它的一些特点也逐步为大家所知,但总体而言比较零散。特别是对于“它是怎么想出来的”、“非得要这个形式不可吗”等原理性问题,还没有比较好的答案。
因此,本文主要围绕这些问题展开思考,可能在思考过程中读者会有跟笔者一样的感觉,即越思考越觉得这个设计之精妙漂亮,让人叹服~








最近评论