3
Feb
[SETI-50周年]茫茫宇宙觅知音
By 苏剑林 | 2011-02-03 | 19942位读者 | 引用转载自2011年1月的《天文爱好者》 作者：薛国轩
“多萝西计划”再探地外文明
据美国空间网站2010年11月13日报道，在人类“探索地外文明”（英文缩写为SETI）50周年纪念之际，世界多个国家的天文学家从本月起再度展开“且听外星人”的联合行动，以延续开始于1960年的“奥兹玛计划”。新的探索活动被命名为“多萝西计划”（Project Dorothy），已于11月5日正式启动，将持续整整一个月时间，来自澳大利亚、日本、韩国、意大利、荷兰、法国、阿根廷和美国的天文学家参与其中。他们将把大大小小的望远镜指向地球周围的一些星球，以期收听到外星人的“天外来音”。
Allen Telescope Array
28
May
科学空间：2011年6月重要天象
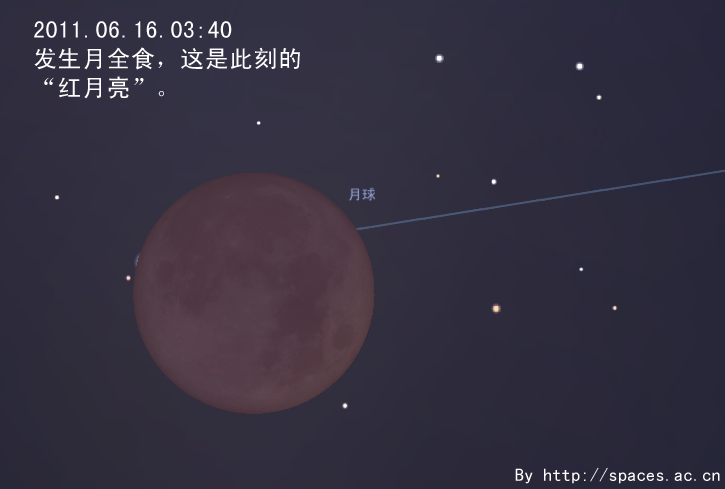
By 苏剑林 | 2011-05-28 | 26660位读者 | 引用
月全食-201106160340
6月中下旬，是北半球一年中黑夜最短的时期。今年6月22日是夏至节气，以北纬40°地区为例，当天天文昏影终到次日天文晨光始的间隔只有不到4小时50分钟。黑夜短暂会使我们可用于天文观测的时间缩短。但在夏至前后，午夜时分太阳也会在地平线下不太低的位置，这样我们就有可能整夜观测到一些类似国际空间站这样的低轨道人造天体。有兴趣的朋友可以查询相关的过境预报，挑战在一晚可以观测到多少次国际空间站过境这类的观测项目。发生在六月的日偏食和月全食，是今年天象的重头戏。接下来笔者就日偏食讲起，跟大家聊聊发生在6月的天象。
19
Feb
《方程与宇宙》:一种有趣的三体问题坐标
By 苏剑林 | 2011-02-19 | 23071位读者 | 引用通常来说，选取惯性系为参考系，列出的三体问题方程为
$$\ddot{\vec{r}}_k=\sum_{i=1,i != k}^{n} Gm_i\frac{\vec{r}_i-\vec{r}_k}{|\vec{r}_i-\vec{r}_k|^3}$$
历史上出现过很多不同形式的变换，使得三体问题的运动方程有了各样的形式，如Lagrange形式、Jacobi形式、Hamilton形式等。这些变换形式都各有特点，都能够在一定程度上化简三体问题。BoJone在研究摆弄等质量型三体问题的运动方程时，也发现了一种很有趣的变换，在此贴出与大家分享。
设$\vec{R}_1=\vec{r}_1-\vec{r}_2,\vec{R}_2=\vec{r}_2-\vec{r}_3,\vec{R}_3=\vec{r}_3-\vec{r}_1$，则三体问题的运动方程变为
19
Apr
《教材如何写》:BoJone的粗浅看法
By 苏剑林 | 2011-04-19 | 21359位读者 | 引用在科学空间所转载的上两篇文章中，matrix67和范翔都表达了他们对大多数现行（数学&物理）教材的不满和对编写教材的一些建议。今天，BoJone也来发发牢骚，说说教材。
首先得说明下，目前BoJone只是一个高二生，或者说，是一个爱好数学、物理的高中生，因此本文所描写的观点仅仅是个人的看法，而且应该带有诸多的不成熟看法。不论如何，谨在此提出，欢迎讨论。
BoJone认为，人类都有着追求利益的倾向，要是一样东西能够对我们有“好处”，给我们带来方便，那么我们就很乐意去拥有它，或者去学习它。数学、物理理论也应当如此，当教材编写者想要引入一个新概念或介绍一个新理论、方法时，首先要做的并不是如何从严格上定义、推导、证明、最后才去应用，而相反，他们应该要大书特书引入新概念和方法后有什么“好处”。只有了解到了它的用处之后，读者才会有明确的目的和足够的心思去进一步的学习。这一步对于一些抽象的理论的学习是很重要的，要不然，那么繁琐、枯燥的推理证明过程会抹杀掉绝大多数人的信心，纵使后来“终于”弄懂了它的用处，也兴趣倍减。说到这里，就不得不批评一下人教版数学选修教材中的一个很让人反感的做法，在《选修2-2》中它引入了复数，但仅仅简单交待了复数的加减乘除运算和模等定义后就了事，对于复数的一些精华，比如复数乘法代表着坐标旋转等，则全然不提，这样的“复数”有何意义呢？有同学问我：“学复数有什么用？”我只能回答：“就目前来说，复数的唯一作用就是增加了我们高考的负担。”
6
Jul
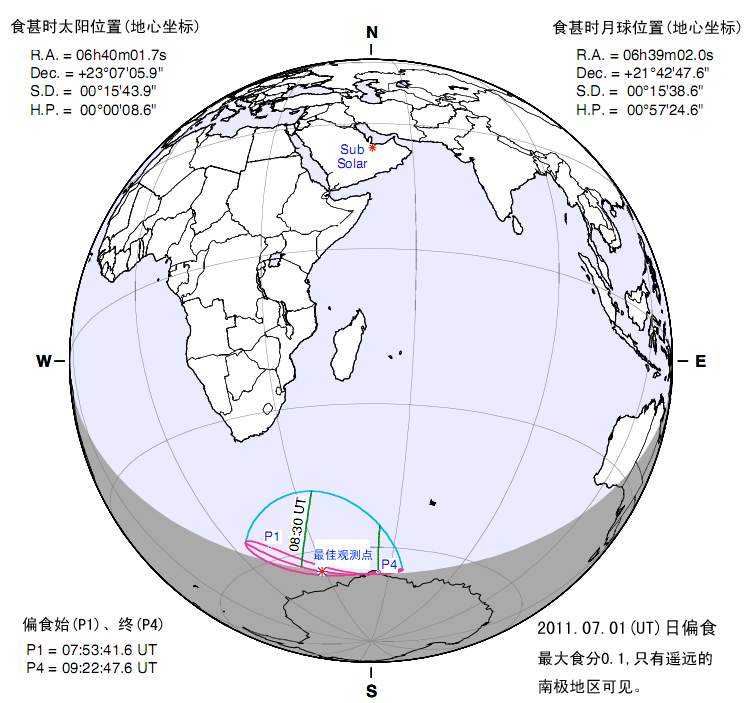
科学空间：2011年7月重要天象
By 苏剑林 | 2011-07-06 | 23002位读者 | 引用
12
Sep
数学竞赛广东预赛|组成三角形的概率
By 苏剑林 | 2011-09-12 | 57520位读者 | 引用九月三日BoJone和九个同学到云浮参加了今年广东省的数学竞赛预赛，那一起出发、玩笑、作战、吃饭的情景依然历历在目，让我久久不能忘怀。是呀，能够并肩作战的感觉真好！九日数学成绩出来了，遗憾的是今年政策改变了，我被告知整个市只有三个名额能够参加复赛，于是新兴只有我一个人进入了复赛（另外两个据说是罗定的，我们三个并列第一）。有点无语，我想，大概是要把那些为了功利而参赛的人都给刷下去吧...
今年广东的预赛题前所未有的简单，不论是和全国其他地方相比还是和上一年的题目相比，都简单了不少，但我还是做得不大理想，据我估计，120分的卷子我顶多能够拿个68分，所以BoJone的基本技能实在不容乐观。从云浮考试回来后，和同行的同学讨论试题，得出了一些很有趣的结果，那过程可谓其乐无穷呀！下面是倒数第二题预赛题的几个绝妙解法，供大家欣赏。解法由我和伍泽麒（人称“兔子、神兔”，人如其名，天资聪颖，性格可爱）完成。
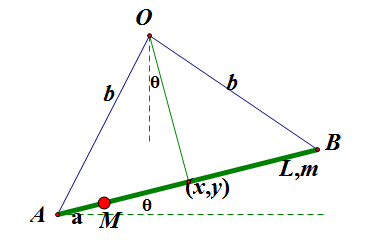
题目：
在一条线段中随意选取两个点，把这条线段截成三段，求这三段线段能够组成一个三角形的概率。
13
Jan
混沌的世界——“星之轨迹”的研究
By 苏剑林 | 2012-01-13 | 38861位读者 | 引用（本文已被刊登在2012年1月的《天文爱好者》上，于笔者而言这是一份很棒的新年礼物！）
在去年第七期《天爱》上，我们看到了N体问题所呈现出来的一些对称、漂亮的周期轨道，这体现了N体问题和谐有序的一面。但是这仅仅是N体问题的冰山一角，笔者也提到过N体问题的本质是混沌、无序的，通俗来讲就是非常乱，无法用数学方程来精确描述。这看起来是一种不完美。但试想，探索当初伽利略将望远镜对准月球后，看到的是如想象中光滑的月面，那么他还会惊叹宇宙的神奇吗？
本文就让我们来更深入地了解一下N体问题的研究历史。
观测&拟合时代
由于人类的自我优越感以及日月星辰东升西落的经验，让我们长期都认为地球是宇宙的中心。第一个比较系统提出地心说的人当属天文学家欧多克斯（Eudoxus，死于公元前347年左右），但他的地心说是非常粗糙的，以至于无法解释很多基本现象，如无法准确预言日食和解释行星逆行等。但亚里士多德接受了地心说，并且由于他在政治和科学上的权威，使地心说免去了夭折的命运。后来托勒密通过他的本轮，完善了地心说，使之延续到了16世纪。
21
Jan
最近评论