7
Jan
【搜出来的文本】⋅（一）从文本生成到搜索采样
By 苏剑林 | 2021-01-07 | 61467位读者 | 引用最近，笔者入了一个新坑：基于离散优化的思想做一些文本生成任务。简单来说，就是把我们要生成文本的目标量化地写下来，构建一个分布，然后搜索这个分布的最大值点或者从这个分布中进行采样，这个过程通常不需要标签数据的训练。由于语言是离散的，因此梯度下降之类的连续函数优化方法不可用，并且由于这个分布通常没有容易采样的形式，直接采样也不可行，因此需要一些特别设计的采样算法，比如拒绝采样（Rejection Sampling）、MCMC（Markov Chain Monte Carlo）、MH采样（Metropolis-Hastings Sampling）、吉布斯采样（Gibbs Sampling），等等。
有些读者可能会觉得有些眼熟，似乎回到了让人头大的学习LDA（Latent Dirichlet Allocation）的那些年？没错，上述采样算法其实也是理解LDA模型的必备基础。本文我们就来回顾这些形形色色的采样算法，它们将会出现在后面要介绍的丰富的文本生成应用中。
9
Feb
一个二值化词向量模型，是怎么跟果蝇搭上关系的？
By 苏剑林 | 2021-02-09 | 26467位读者 | 引用
果蝇（图片来自Google搜索）
可能有些读者最近会留意到ICLR 2021的论文《Can a Fruit Fly Learn Word Embeddings?》，文中写到它是基于仿生思想（仿果蝇的嗅觉回路）做出来的一个二值化词向量模型。其实论文的算法部分并不算难读，可能整篇论文读下来大家的最主要疑惑就是“这东西跟果蝇有什么关系？”、“作者真是从果蝇里边受到启发的？”等等。本文就让我们来追寻一下该算法的来龙去脉，试图回答一下这个词向量模型是怎么跟果蝇搭上关系的。
BioWord
原论文并没有给该词向量模型起个名字，为了称呼上的方便，这里笔者就自作主张将其称为“BioWord”了。总的来说，论文内容大体上有三部分：
1、给每个n-gram构建了一个词袋表示向量；
2、对这些n-gram向量执行BioHash算法，得到所谓的（二值化的）静态/动态词向量；
3、“拼命”讲了一个故事。
3
Feb
让研究人员绞尽脑汁的Transformer位置编码
By 苏剑林 | 2021-02-03 | 193774位读者 | 引用不同于RNN、CNN等模型，对于Transformer模型来说，位置编码的加入是必不可少的，因为纯粹的Attention模块是无法捕捉输入顺序的，即无法区分不同位置的Token。为此我们大体有两个选择：1、想办法将位置信息融入到输入中，这构成了绝对位置编码的一般做法；2、想办法微调一下Attention结构，使得它有能力分辨不同位置的Token，这构成了相对位置编码的一般做法。
虽然说起来主要就是绝对位置编码和相对位置编码两大类，但每一类其实又能衍生出各种各样的变种，为此研究人员可算是煞费苦心、绞尽脑汁了，此外还有一些不按套路出牌的位置编码。本文就让我们来欣赏一下研究人员为了更好地表达位置信息所构建出来的“八仙过海，各显神通”般的编码方案。
绝对位置编码
形式上来看，绝对位置编码是相对简单的一种方案，但即便如此，也不妨碍各路研究人员的奇思妙想，也有不少的变种。一般来说，绝对位置编码会加到输入中：在输入的第$k$个向量$\boldsymbol{x}_k$中加入位置向量$\boldsymbol{p}_k$变为$\boldsymbol{x}_k + \boldsymbol{p}_k$，其中$\boldsymbol{p}_k$只依赖于位置编号$k$。
16
Feb
Nyströmformer：基于矩阵分解的线性化Attention方案
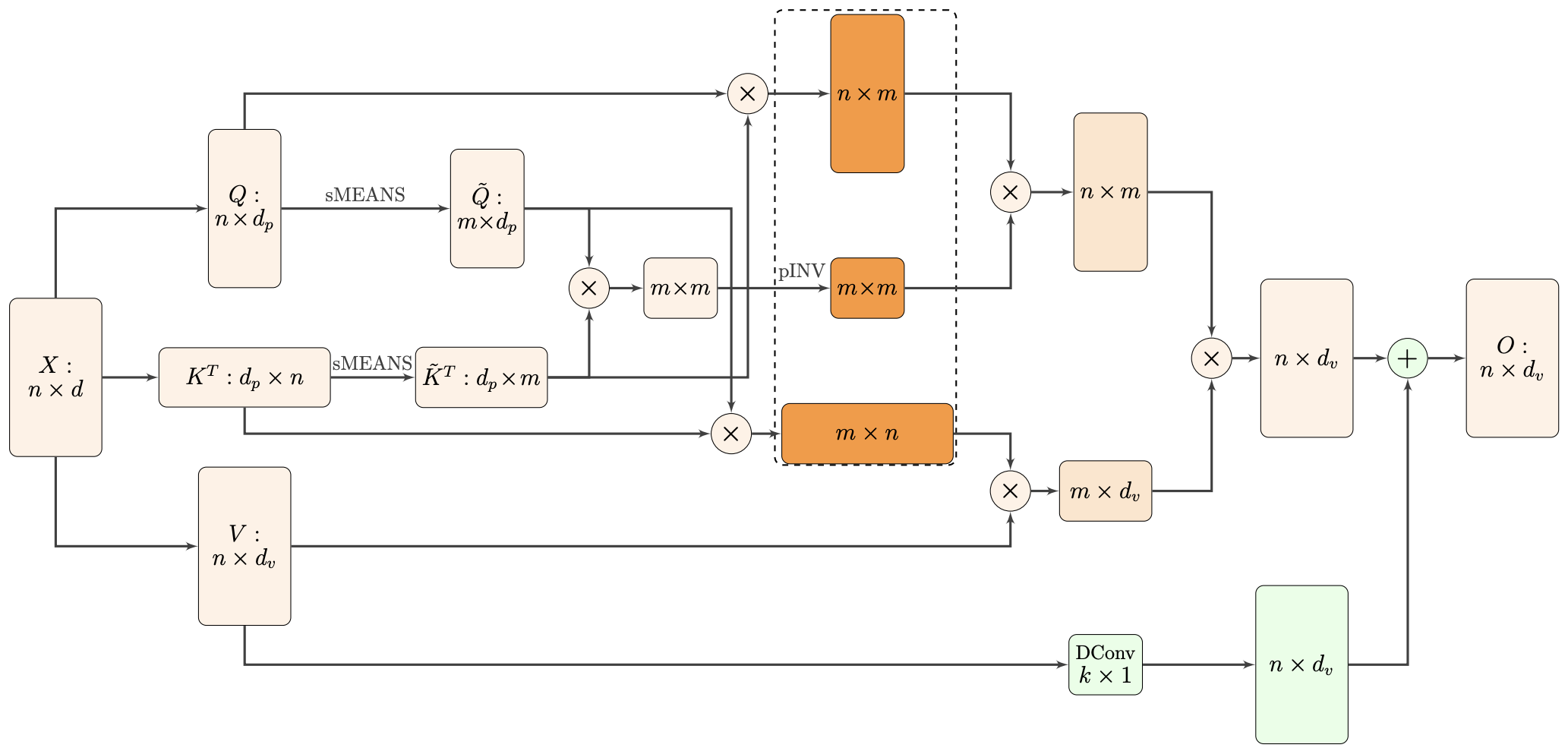
By 苏剑林 | 2021-02-16 | 44587位读者 | 引用标准Attention的$\mathcal{O}(n^2)$复杂度可真是让研究人员头大。前段时间我们在博文《Performer：用随机投影将Attention的复杂度线性化》中介绍了Google的Performer模型，它通过随机投影的方式将标准Attention转化为线性Attention。无独有偶，前些天Arxiv上放出了AAAI 2021的一篇论文《Nyströmformer: A Nyström-Based Algorithm for Approximating Self-Attention》，里边又提出了一种从另一个角度把标准Attention线性化的方案。
Nyströmformer结构示意图
该方案写的是Nyström-Based，顾名思义是利用了Nyström方法来近似标准Attention的。但是坦白说，在看到这篇论文之前，笔者也完全没听说过Nyström方法，而纵观整篇论文，里边也全是笔者一眼看上去感觉很茫然的矩阵分解推导，理解起来颇为困难。不过有趣的是，尽管作者的推导很复杂，但笔者发现最终的结果可以通过一个相对来说更简明的方式来理解，遂将笔者对Nyströmformer的理解整理在此，供大家参考。
8
Jul
两个多元正态分布的KL散度、巴氏距离和W距离
By 苏剑林 | 2021-07-08 | 102779位读者 | 引用正态分布是最常见的连续型概率分布之一。它是给定均值和协方差后的最大熵分布（参考《“熵”不起：从熵、最大熵原理到最大熵模型（二）》），也可以看作任意连续型分布的二阶近似，它的地位就相当于一般函数的线性近似。从这个角度来看，正态分布算得上是最简单的连续型分布了。也正因为简单，所以对于很多估计量来说，它都能写出解析解来。
本文主要来计算两个多元正态分布的几种度量，包括KL散度、巴氏距离和W距离，它们都有显式解析解。
正态分布
这里简单回顾一下正态分布的一些基础知识。注意，仅仅是回顾，这还不足以作为正态分布的入门教程。
概率密度
正态分布，也即高斯分布，是定义在$\mathbb{R}^n$上的连续型概率分布，其概率密度函数为
\begin{equation}p(\boldsymbol{x})=\frac{1}{\sqrt{(2\pi)^n \det(\boldsymbol{\Sigma})}}\exp\left\{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\top}\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right\}\end{equation}
1
Jul
又是Dropout两次！这次它做到了有监督任务的SOTA
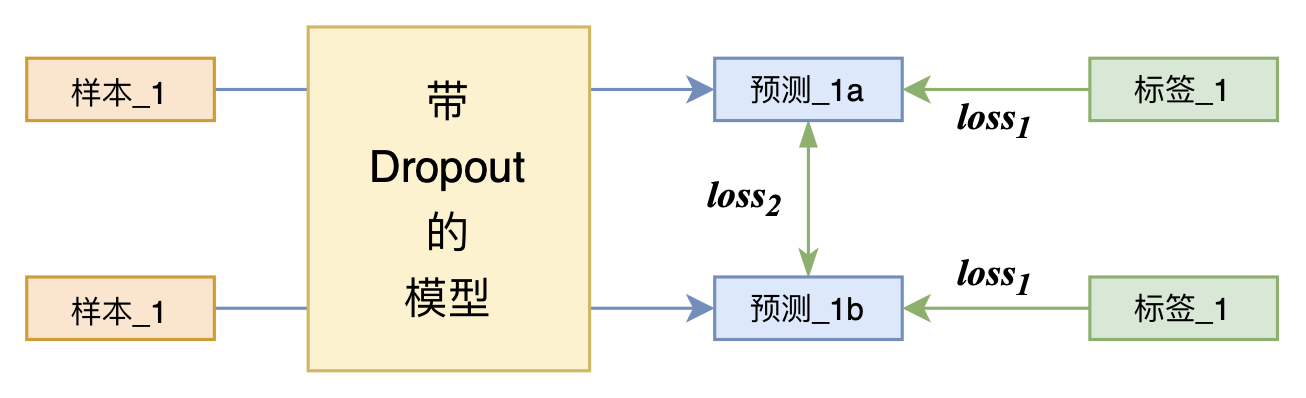
By 苏剑林 | 2021-07-01 | 209003位读者 | 引用关注NLP新进展的读者，想必对四月份发布的SimCSE印象颇深，它通过简单的“Dropout两次”来构造正样本进行对比学习，达到了无监督语义相似度任务的全面SOTA。无独有偶，最近的论文《R-Drop: Regularized Dropout for Neural Networks》提出了R-Drop，它将“Dropout两次”的思想用到了有监督任务中，每个实验结果几乎都取得了明显的提升。此外，笔者在自己的实验还发现，它在半监督任务上也能有不俗的表现。
R-Drop示意图
小小的“Dropout两次”，居然跑出了“五项全能”的感觉，不得不令人惊讶。本文来介绍一下R-Drop，并分享一下笔者对它背后原理的思考。
5
Mar
短文本匹配Baseline：脱敏数据使用预训练模型的尝试
By 苏剑林 | 2021-03-05 | 106059位读者 | 引用最近凑着热闹玩了玩全球人工智能技术创新大赛中的“小布助手对话短文本语义匹配”赛道，其任务就是常规的短文本句子对二分类任务，这任务在如今各种预训练Transformer“横行”的时代已经没啥什么特别的难度了，但有意思的是，这次比赛脱敏了，也就是每个字都被影射为数字ID了，我们无法得到原始文本。
在这种情况下，还能用BERT等预训练模型吗？用肯定是可以用的，但需要一些技巧，并且可能还需要再预训练一下。本文分享一个baseline，它将分类、预训练和半监督学习都结合在了一起，能够用于脱敏数据任务。
本文模型示意图
24
Sep
让人惊叹的Johnson-Lindenstrauss引理：应用篇
By 苏剑林 | 2021-09-24 | 35710位读者 | 引用上一篇文章中，我们比较详细地介绍了Johnson-Lindenstrauss引理（JL引理）的理论推导，这一篇我们来关注它的应用。
作为一个内容上本身就跟降维相关的结论，JL引理最基本的自然就是作为一个降维方法来用。但除了这个直接应用外，很多看似不相关的算法，比如局部敏感哈希（LSH）、随机SVD等，本质上也依赖于JL引理。此外，对于机器学习模型来说，JL引理通常还能为我们的维度选择提供一些理论解释。
降维的工具
JL引理提供了一个非常简单直接的“随机投影”降维思路：
给定$N$个向量$v_1,v_2,\cdots,v_N\in\mathbb{R}^m$，如果想要将它降到$n$维，那么只需要从$\mathcal{N}(0,1/n)$中采样一个$n\times m$矩阵$A$，然后$Av_1,Av_2,\cdots,Av_N$就是降维后的结果。
最近评论