科学空间|Scientific Spaces

主方程（master equation）是对随机过程进行建模的重要方法，它代表着马尔科夫过程的微分形式，我们的专业主要工具之一就是主方程，说宏大一点，量子力学和统计力学等也不外乎是主方程的一个特例。

然而，笔者阅读了几个著作，比如《统计物理现代教程》，还有我导师的《生物系统的随机动力学》，我发现这些著作对于主方程的推导都很模糊，他们在着力解释结果的意义，但并不说明结果的思想来源，因此其过程难以让人信服。而知乎上有人提问《如何理解马尔科夫过程的主方程的推导过程？》但没有得到很好的答案，也表明了这个事实。

马尔可夫过程

主方程是用来描述马尔科夫过程的，而马尔科夫过程可以理解为运动的无记忆性，说通俗点，就是下一刻的概率分布，只跟当前时刻有关，跟历史状态无关。用概率公式写出来就是（这里只考虑连续型概率，因此这里的$p$是概率密度）：
$$\begin{equation}\label{eq:maerkefu}p(x,\tau)=\int p(x,\tau|y,t) p(y,t) dy\end{equation}$$
这里的积分区域是全空间。这里的$p(x,\tau|y,t)$称为跃迁概率，即已经确定了$t$时刻来到了$y$位置后、在$\tau$时刻达到$x$的概率密度，这个式子的物理意义是很明显的，就不多做解释了。

点击阅读全文...

在有监督的机器学习中，经常会说到训练集（train)、验证集（validation）和测试集（test），这三个集合的区分可能会让人糊涂，特别是，有些读者搞不清楚验证集和测试集有什么区别。

划分

如果我们自己已经有了一个大的标注数据集，想要完成一个有监督模型的测试，那么通常使用均匀随机抽样的方式，将数据集划分为训练集、验证集、测试集，这三个集合不能有交集，常见的比例是8:1:1，当然比例是人为的。从这个角度来看，三个集合都是同分布的。

点击阅读全文...

最后，我们来看一下词向量模型$(15)$会有什么好的性质，或者说，如此煞费苦心去构造一个新的词向量模型，会得到什么回报呢？

模长的含义

似乎所有的词向量模型中，都很少会关心词向量的模长。有趣的是，我们上述词向量模型得到的词向量，其模长还能在一定程度上代表着词的重要程度。我们可以从两个角度理解这个事实。

在一个窗口内的上下文，中心词重复出现概率其实是不大的，是一个比较随机的事件，因此可以粗略地认为
\[P(w,w) \sim P(w)\tag{24}\]
所以根据我们的模型，就有
\[e^{\langle\boldsymbol{v}_{w},\boldsymbol{v}_{w}\rangle} =\frac{P(w,w)}{P(w)P(w)}\sim \frac{1}{P(w)}\tag{25}\]
所以
\[\Vert\boldsymbol{v}_{w}\Vert^2 \sim -\log P(w)\tag{26}\]
可见，词语越高频（越有可能就是停用词、虚词等），对应的词向量模长就越小，这就表明了这种词向量的模长确实可以代表词的重要性。事实上，$-\log P(w)$这个量类似IDF，有个专门的名称叫ICF，请参考论文《TF-ICF: A New Term Weighting Scheme for Clustering Dynamic Data Streams》。

点击阅读全文...

损失函数

现在，我们来定义loss，以便把各个词向量求解出来。用$\tilde{P}$表示$P$的频率估计值，那么我们可以直接以下式为loss
\[\sum_{w_i,w_j}\left(\langle \boldsymbol{v}_i, \boldsymbol{v}_j\rangle-\log\frac{\tilde{P}(w_i,w_j)}{\tilde{P}(w_i)\tilde{P}(w_j)}\right)^2\tag{16}\]
相比之下，无论在参数量还是模型形式上，这个做法都比glove要简单，因此称之为simpler glove。glove模型是
\[\sum_{w_i,w_j}\left(\langle \boldsymbol{v}_i, \boldsymbol{\hat{v}}_j\rangle+b_i+\hat{b}_j-\log X_{ij}\right)^2\tag{17}\]
在glove模型中，对中心词向量和上下文向量做了区分，然后最后模型建议输出的是两套词向量的求和，据说这效果会更好，这是一个比较勉强的trick，但也不是什么毛病。最大的问题是参数$b_i,\hat{b}_j$也是可训练的，这使得模型是严重不适定的！我们有
\[\begin{aligned}&\sum_{w_i,w_j}\left(\langle \boldsymbol{v}_i, \boldsymbol{\hat{v}}_j\rangle+b_i+\hat{b}_j-\log \tilde{P}(w_i,w_j)\right)^2\\
=&\sum_{w_i,w_j}\left[\langle \boldsymbol{v}_i+\boldsymbol{c}, \boldsymbol{\hat{v}}_j+\boldsymbol{c}\rangle+\Big(b_i-\langle \boldsymbol{v}_i, \boldsymbol{c}\rangle - \frac{|\boldsymbol{c}|^2}{2}\Big)\right.\\
&\qquad\qquad\qquad\qquad\left.+\Big(\hat{b}_j-\langle \boldsymbol{\hat{v}}_j, \boldsymbol{c}\rangle - \frac{|\boldsymbol{c}|^2}{2}\Big)-\log X_{ij}\right]^2\end{aligned}\tag{18}\]
这就是说，如果你有了一组解，那么你将所有词向量加上任意一个常数向量后，它还是一组解！这个问题就严重了，我们无法预估得到的是哪组解，一旦加上的是一个非常大的常向量，那么各种度量都没意义了（比如任意两个词的cos值都接近1）。事实上，对glove生成的词向量进行验算就可以发现，glove生成的词向量，停用词的模长远大于一般词的模长，也就是说一堆词放在一起时，停用词的作用还明显些，这显然是不利用后续模型的优化的。（虽然从目前的关于glove的实验结果来看，是我强迫症了一些。）

互信息估算

点击阅读全文...

2017年中，有两篇类似同时也是笔者非常欣赏的论文，分别是FaceBook的《Convolutional Sequence to Sequence Learning》和Google的《Attention is All You Need》，它们都算是Seq2Seq上的创新，本质上来说，都是抛弃了RNN结构来做Seq2Seq任务。

这篇博文中，笔者对《Attention is All You Need》做一点简单的分析。当然，这两篇论文本身就比较火，因此网上已经有很多解读了（不过很多解读都是直接翻译论文的，鲜有自己的理解），因此这里尽可能多自己的文字，尽量不重复网上各位大佬已经说过的内容。

序列编码

深度学习做NLP的方法，基本上都是先将句子分词，然后每个词转化为对应的词向量序列。这样一来，每个句子都对应的是一个矩阵$\boldsymbol{X}=(\boldsymbol{x}_1,\boldsymbol{x}_2,\dots,\boldsymbol{x}_t)$，其中$\boldsymbol{x}_i$都代表着第$i$个词的词向量（行向量），维度为$d$维，故$\boldsymbol{X}\in \mathbb{R}^{n\times d}$。这样的话，问题就变成了编码这些序列了。

第一个基本的思路是RNN层，RNN的方案很简单，递归式进行：
\begin{equation}\boldsymbol{y}_t = f(\boldsymbol{y}_{t-1},\boldsymbol{x}_t)\end{equation}
不管是已经被广泛使用的LSTM、GRU还是最近的SRU，都并未脱离这个递归框架。RNN结构本身比较简单，也很适合序列建模，但RNN的明显缺点之一就是无法并行，因此速度较慢，这是递归的天然缺陷。另外我个人觉得RNN无法很好地学习到全局的结构信息，因为它本质是一个马尔科夫决策过程。

点击阅读全文...

Geoffrey Hinton在谷歌多伦多办公室

由深度学习先驱Hinton开源的Capsule论文《Dynamic Routing Between Capsules》，无疑是去年深度学习界最热点的消息之一。得益于各种媒体的各种吹捧，Capsule被冠以了各种神秘的色彩，诸如“抛弃了梯度下降”、“推倒深度学习重来”等字眼层出不穷，但也有人觉得Capsule不外乎是一个新的炒作概念。

本文试图揭开让人迷惘的云雾，领悟Capsule背后的原理和魅力，品尝这一顿Capsule盛宴。同时，笔者补做了一个自己设计的实验，这个实验能比原论文的实验更有力说明Capsule的确产生效果了。

菜谱一览：

1、Capsule是什么？

2、Capsule为什么要这样做？

3、Capsule真的好吗？

4、我觉得Capsule怎样？

5、若干小菜。

点击阅读全文...

在本文中，我们再次对Capsule进行一次分析。

整体上来看，Capsule算法的细节不是很复杂，对照着它的流程把Capsule用框架实现它基本是没问题的。所以，困难的问题是理解Capsule究竟做了什么，以及为什么要这样做，尤其是Dynamic Routing那几步。

为什么我要反复对Capsule进行分析？这并非单纯的“炒冷饭”，而是为了得到对Capsule原理的理解。众所周知，Capsule给人的感觉就是“有太多人为约定的内容”，没有一种“虽然我不懂，但我相信应该就是这样”的直观感受。我希望尽可能将Capsule的来龙去脉思考清楚，使我们能觉得Capsule是一个自然、流畅的模型，甚至对它举一反三。

在《揭开迷雾，来一顿美味的Capsule盛宴》中，笔者先分析了动态路由的结果，然后指出输出是输入的某种聚类，这个“从结果到原因”的过程多多少少有些望文生义的猜测成分；这次则反过来，直接确认输出是输入的聚类，然后反推动态路由应该是怎样的，其中含糊的成分大大减少。两篇文章之间有一定的互补作用。

点击阅读全文...

事实上，在论文《Dynamic Routing Between Capsules》发布不久后，一篇新的Capsule论文《Matrix Capsules with EM Routing》就已经匿名公开了（在ICLR 2018的匿名评审中），而如今作者已经公开，他们是Geoffrey Hinton, Sara Sabour, Nicholas Frosst。不出大家意料，作者果然有Hinton。

大家都知道，像Hinton这些“鼻祖级”的人物，发表出来的结果一般都是比较“重磅”的。那么，这篇新论文有什么特色呢？

在笔者的思考过程中，文章《Understanding Matrix capsules with EM Routing 》给了我颇多启示，知乎上各位大神的相关讨论也加速了我的阅读，在此表示感谢。

论文摘要

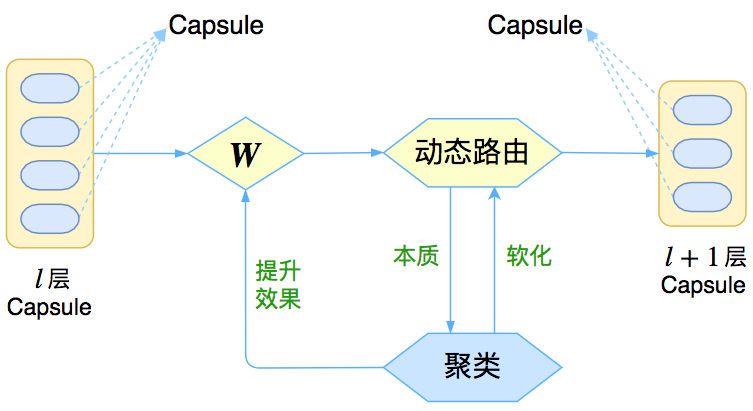
让我们先来回忆一下上一篇介绍《再来一顿贺岁宴：从K-Means到Capsule》中的那个图

Capsule框架的简明示意图

这个图表明，Capsule事实上描述了一个建模的框架，这个框架中的东西很多都是可以自定义的，最明显的是聚类算法，可以说“有多少种聚类算法就有多少种动态路由”。那么这次Hinton修改了什么呢？总的来说，这篇新论文有以下几点新东西：

1、原来用向量来表示一个Capsule，现在用矩阵来表示；

2、聚类算法换成了GMM（高斯混合模型）；

3、在实验部分，实现了Capsule版的卷积。

点击阅读全文...