科学空间|Scientific Spaces

在矩阵压缩这个问题上，我们通常有两个策略可以选择，分别是低秩化和稀疏化。低秩化通过寻找矩阵的低秩近似来减少矩阵尺寸，而稀疏化则是通过减少矩阵中的非零元素来降低矩阵的复杂性。如果说SVD是奔着矩阵的低秩近似去的，那么相应地寻找矩阵稀疏近似的算法又是什么呢？

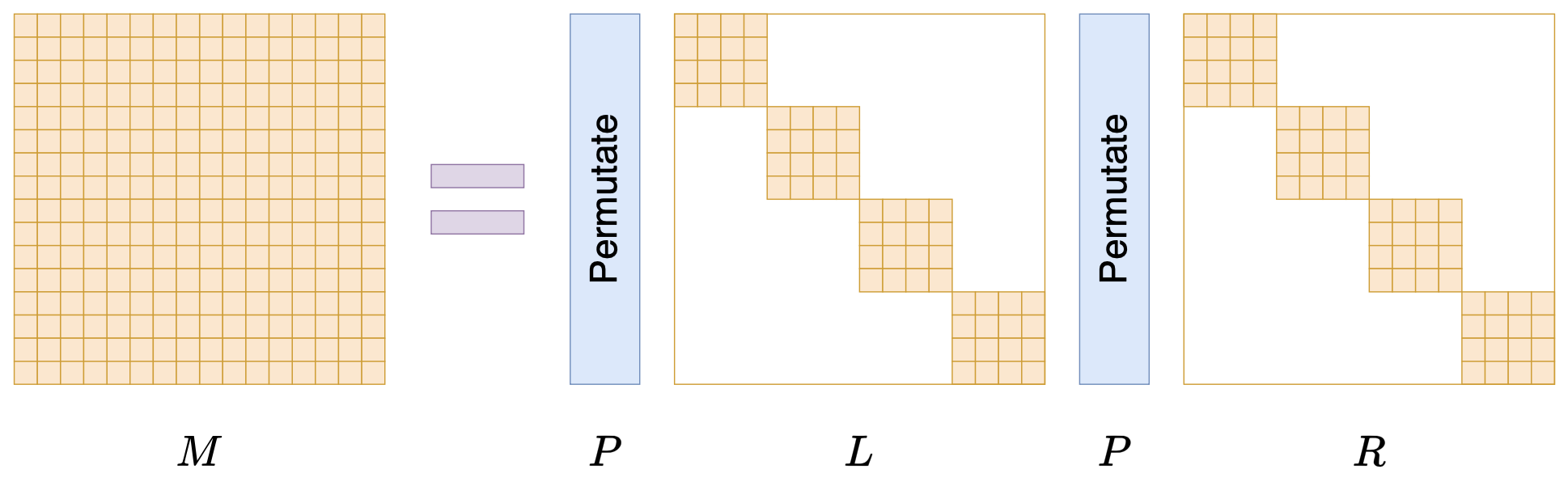
接下来我们要学习的是论文《Monarch: Expressive Structured Matrices for Efficient and Accurate Training》，它为上述问题给出了一个答案——“Monarch矩阵”，这是一簇能够分解为若干置换矩阵与稀疏矩阵乘积的矩阵，同时具备计算高效且表达能力强的特点，论文还讨论了如何求一般矩阵的Monarch近似，以及利用Monarch矩阵参数化LLM来提高LLM速度等内容。

Monarch矩阵形式M=PLPR

值得指出的是，该论文的作者也正是著名的Flash Attention的作者Tri Dao，其工作几乎都在致力于改进LLM的性能，这篇Monarch也是他主页上特意展示的几篇论文之一，单从这一点看就非常值得学习一番。

点击阅读全文...

我现在是越来越佩服爱因斯坦了，他的相对论是他天才的思想的充分体现。只有当相对论提出之后，宏观物理的大多数现象和规律才得到了统一的描述。狭义相对论中爱因斯坦对我们速度叠加常识的否定已经显示了他莫大的勇气，而一项头脑风暴性的工作——广义相对论则将他惊人的创造力体现得完美无瑕。我是被量子力学的数学吸引的，于相对论则是被相对论美妙的逻辑体系吸引。当然，其中也有相当美妙的数学。

狭义相对论中的核心内容之一就是被称为洛仑兹变换的东西，这在相对论发表之前已经由洛仑兹推导出来了，只不过他不承认他的物理意义，也就没有就此进行一次物理革命，革命的任务则由爱因斯坦完成。很久前我就已经看过洛仑兹变换的推导，那是直接设一种线性关系来求解的。但是我总感觉那样的推导不够清晰（也许是我的理解方式有问题吧），而且没有说明狭义相对论的两条原理如何体现出现。所以在研究过矩阵之后，我就尝试用矩阵来推导洛仑兹变换，发现效果挺好的，而且我觉得能够体现出相对论中的对称性。

两条原理

1、狭义相对性原理：在所有惯性系中，物理定律有相同的表达形式。这是力学相对性原理的推广，它适用于一切物理定律，其本质是所有惯性系平权。

2、光速不变原理：所有惯性系中，真空中的光速都等于c=299 792 458 m/s，与光源运动无关。迈克耳孙-莫雷实验是其有力证明。

点击阅读全文...

前言：我小学开始就喜欢纯数学，后来也喜欢上物理，还学习过一段时间的理论物理，直到本科毕业时，我才慢慢进入机器学习领域。所以，哪怕在机器学习领域中，我的研究习惯还保留着数学和物理的风格：企图从最少的原理出发，理解、推导尽可能多的东西。这篇文章是我这个理念的结果之一，试图以变分推断作为出发点，来统一地理解深度学习中的各种模型，尤其是各种让人眼花缭乱的GAN。本文已经挂到arxiv上，需要读英文原稿的可以移步到《Variational Inference: A Unified Framework of Generative Models and Some Revelations》。

下面是文章的介绍。其实，中文版的信息可能还比英文版要稍微丰富一些，原谅我这蹩脚的英语...

摘要：本文从一种新的视角阐述了变分推断，并证明了EM算法、VAE、GAN、AAE、ALI(BiGAN)都可以作为变分推断的某个特例。其中，论文也表明了标准的GAN的优化目标是不完备的，这可以解释为什么GAN的训练需要谨慎地选择各个超参数。最后，文中给出了一个可以改善这种不完备性的正则项，实验表明该正则项能增强GAN训练的稳定性。

近年来，深度生成模型，尤其是GAN，取得了巨大的成功。现在我们已经可以找到数十个乃至上百个GAN的变种。然而，其中的大部分都是凭着经验改进的，鲜有比较完备的理论指导。

本文的目标是通过变分推断来给这些生成模型建立一个统一的框架。首先，本文先介绍了变分推断的一个新形式，这个新形式其实在博客以前的文章中就已经介绍过，它可以让我们在几行字之内导出变分自编码器（VAE）和EM算法。然后，利用这个新形式，我们能直接导出GAN，并且发现标准GAN的loss实则是不完备的，缺少了一个正则项。如果没有这个正则项，我们就需要谨慎地调整超参数，才能使得模型收敛。

点击阅读全文...

本节简单介绍用矩阵来描述旋转。在二维平面上，复数无疑是描述旋转的最佳工具；然而推广到三维空间中，却要动用到“四元数”了。为了证明四元数的相关结论，我们需要三维旋转的矩阵描述。最一般的旋转运动为：绕某一根轴旋转$\theta$角度。这样我们就需要三个参数来描述它：确定一根轴至少需要两个参数，确定角度需要一个参数。因此，如果要用“数”来描述三维空间的伸缩和旋转的话，“三元数”显然是不够的，完成这一目的至少需要四元数。这也从另外一个角度反映了三元数的不存在性。

矩阵方法
首先我们认识到，如果旋转轴是坐标轴之一，那么旋转矩阵将是最简单的，比如向量$\boldsymbol{x}=(x_0,y_0,z_0)^{T}$绕$z$轴逆时针旋转$\theta$角后的坐标就可以描述为
$$\begin{equation}
\boldsymbol{R}_{\theta}\boldsymbol{x}\end{equation}$$

点击阅读全文...

几年前，笔者曾经以自己对矩阵的粗浅理解写了一个“理解矩阵”系列，其中有一篇《为什么只有方阵有行列式？》讨论了非方阵的行列式问题，里边给出了“非方针的行列式不好看”和“方阵的行列式就够了”的观点。本文来再次思考这个问题。

首先回顾方阵的行列式，其实行列式最重要的价值在于它的几何意义：

n维方阵的行列式的绝对值，等于它的各个行（或列）向量所张成的n维立体的超体积。

这个几何意义是行列式的一切重要性的源头，相关的讨论可以参考《行列式的点滴》，它也是我们讨论非方阵行列式的基础。

分析

对于方阵$\boldsymbol{A}_{n\times n}$来说，可以将它看成$n$个行向量的组合，也可以看成$n$个列向量的组合，不管是哪一种，行列式的绝对值都等于这$n$个向量所张成的$n$维立体的超体积。换句话说，对于方阵来说，行、列向量的区分不改变行列式。

对于非方阵$\boldsymbol{B}_{n \times k}$就不一样了，不失一般性，假设$n > k$。我们可以将它看成$n$个$k$维行向量的组合，也可以看成$k$个$n$维列向量的组合。非方针的行列式，应该也具有同样含义，即它们所张成的立体的超体积。

我们来看第一种情况，如果看成$n$个$k$维行向量，那么就得视为这$n$个向量张成的$n$维体的超体积了，但是要注意$n > k$，因此这$n$个向量必然线性相关，因此它们根本就张不成一个$n$维体，也许是一个$n-1$维体甚至更低，这样一来，它的$n$维体的超体积自然为0。

但是第二种情况就没有那么平凡了。如果看成$k$个$n$维列向量，那么这$k$个向量虽然是$n$维的，但它们张成的是一个$k$维体，这$k$维体的超体积未必为0。我们就以这个非平凡的体积作为非方阵行列式的定义好了。

点击阅读全文...

最近笔者做了一些理解和改进Transformer的尝试，得到了一些似乎还有价值的经验和结论，遂开一个专题总结一下，命名为“Transformer升级之路”，既代表理解上的深入，也代表结果上的改进。

作为该专题的第一篇文章，笔者将会介绍自己对Google在《Attention is All You Need》中提出来的Sinusoidal位置编码
\begin{equation}\left\{\begin{aligned}&\boldsymbol{p}_{k,2i}=\sin\Big(k/10000^{2i/d}\Big)\\
&\boldsymbol{p}_{k, 2i+1}=\cos\Big(k/10000^{2i/d}\Big)
\end{aligned}\right.\label{eq:sin}\end{equation}
的新理解，其中$\boldsymbol{p}_{k,2i},\boldsymbol{p}_{k,2i+1}$分别是位置$k$的编码向量的第$2i,2i+1$个分量，$d$是向量维度。

作为位置编码的一个显式解，Google在原论文中对它的描述却寥寥无几，只是简单提及了它可以表达相对位置信息，后来知乎等平台上也出现了一些解读，它的一些特点也逐步为大家所知，但总体而言比较零散。特别是对于“它是怎么想出来的”、“非得要这个形式不可吗”等原理性问题，还没有比较好的答案。

因此，本文主要围绕这些问题展开思考，可能在思考过程中读者会有跟笔者一样的感觉，即越思考越觉得这个设计之精妙漂亮，让人叹服～

点击阅读全文...

在上一篇文章中，我们以矩阵的方式推导出了洛仑兹变换。矩阵表述不仅仅具有形式上的美，还具有很重要的实用价值，比如可以很方便地寻找各种不变量。当洛仑兹变换用矩阵的方式表达出来后，很多线性代数中已知的理论都可以用在上边。在这篇小小的续集中，我们将尝试阐述这个思想。

本文中，继续设光速$c=1$。

我们已经得到了洛仑兹变换的矩阵形式：
\begin{equation}\left[\begin{array}{c} x\\t \end{array}\right]=\frac{1}{\sqrt{1-v^2}}\left[\begin{array}{c c}1 & v\\ v & 1 \end{array}\right]\left[\begin{array}{c}x'\\t' \end{array}\right]\end{equation}

点击阅读全文...

作为量子理论的一个重要定理，不确定性原理总是伴随着物理意义出现的，但是从数学的角度来讲，把不确定性原理的数学形式抽象出来，有助于我们发现更多领域的“不确定性原理”。

本文中，我们将谈及不确定性原理的n维矩阵形式。首先需要解释给大家的是，不确定性原理其实是关于“两个厄密算符与一个单位向量之间的一条不等式”。在量子力学中，厄密算符对应着无穷维的厄密矩阵；而所谓厄密矩阵，就是一个矩阵同时取共轭和转置之后，等于它自身。但是本文讨论一个更简单的情况，那就是n维实矩阵，n维实矩阵中的厄密矩阵就是我们所说的实对称矩阵了。

设$\boldsymbol{x}$是一个$n$维单位向量，即$|\boldsymbol{x}|=1$，而$\boldsymbol{A}$和$\boldsymbol{B}$是n阶实对称矩阵。在量子力学中，$\boldsymbol{x}$就是波函数，但是在这里，它只不过是一个单位实向量；并记$\boldsymbol{I}$是$n$阶单位阵。

考虑
$$\bar{A}=\boldsymbol{x}^{T}\boldsymbol{A}\boldsymbol{x},\bar{B}=\boldsymbol{x}^{T}\boldsymbol{B}\boldsymbol{x}$$
从这些记号可以看出，这些量对应着可观测量的期望值。当然，如果不懂量子力学，可以只看上面的矩阵形式。

点击阅读全文...