线性Attention的探索:Attention必须有个Softmax吗?
By 苏剑林 | 2020-07-04 | 216059位读者 | 引用众所周知,尽管基于Attention机制的Transformer类模型有着良好的并行性能,但它的空间和时间复杂度都是$\mathcal{O}(n^2)$级别的,$n$是序列长度,所以当$n$比较大时Transformer模型的计算量难以承受。近来,也有不少工作致力于降低Transformer模型的计算量,比如模型剪枝、量化、蒸馏等精简技术,又或者修改Attention结构,使得其复杂度能降低到$\mathcal{O}(n\log n)$甚至$\mathcal{O}(n)$。
前几天笔者读到了论文《Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention》,了解到了线性化Attention(Linear Attention)这个探索点,继而阅读了一些相关文献,有一些不错的收获,最后将自己对线性化Attention的理解汇总在此文中。
Attention
当前最流行的Attention机制当属Scaled-Dot Attention,形式为
\begin{equation}Attention(\boldsymbol{Q},\boldsymbol{K},\boldsymbol{V}) = softmax\left(\boldsymbol{Q}\boldsymbol{K}^{\top}\right)\boldsymbol{V}\label{eq:std-att}\end{equation}
这里的$\boldsymbol{Q}\in\mathbb{R}^{n\times d_k}, \boldsymbol{K}\in\mathbb{R}^{m\times d_k}, \boldsymbol{V}\in\mathbb{R}^{m\times d_v}$,简单起见我们就没显式地写出Attention的缩放因子了。本文我们主要关心Self Attention场景,所以为了介绍上的方便统一设$\boldsymbol{Q}, \boldsymbol{K}, \boldsymbol{V}\in\mathbb{R}^{n\times d}$,一般场景下都有$n > d$甚至$n\gg d$(BERT base里边$d=64$)。
BERT-of-Theseus:基于模块替换的模型压缩方法
By 苏剑林 | 2020-07-17 | 90600位读者 | 引用最近了解到一种称为“BERT-of-Theseus”的BERT模型压缩方法,来自论文《BERT-of-Theseus: Compressing BERT by Progressive Module Replacing》。这是一种以“可替换性”为出发点所构建的模型压缩方案,相比常规的剪枝、蒸馏等手段,它整个流程显得更为优雅、简洁。本文将对该方法做一个简要的介绍,给出一个基于bert4keras的实现,并验证它的有效性。
模型压缩
首先,我们简要介绍一下模型压缩。不过由于笔者并非专门做模型压缩的,也没有经过特别系统的调研,所以该介绍可能显得不专业,请读者理解。
也来扯几句“全国青少年科技创新大赛”
By 苏剑林 | 2020-07-18 | 33974位读者 | 引用通过互信息思想来缓解类别不平衡问题
By 苏剑林 | 2020-07-19 | 152635位读者 | 引用类别不平衡问题,也叫“长尾问题”,是机器学习面临的常见问题之一,尤其是来源于真实场景下的数据集,几乎都是类别不平衡的。大概在两年前,笔者也思考过这个问题,当时正好对“互信息”相关的内容颇有心得,所以构思了一种基于互信息思想的解决办法,但又想了一下,那思路似乎过于平凡,所以就没有深究。然而,前几天在arxiv上刷到Google的一篇文章《Long-tail learning via logit adjustment》,意外地发现里边包含了跟笔者当初的构思几乎一样的方法,这才意识到当初放弃的思路原来还能达到SOTA的水平~于是结合这篇论文,将笔者当初的构思过程整理于此,希望不会被读者嫌弃“马后炮”。
问题描述
这里主要关心的是单标签的多分类问题,假设有$1,2,\cdots,K$共$K$个候选类别,训练数据为$(x,y)\sim\mathcal{D}$,建模的分布为$p_{\theta}(y|x)$,那么我们的优化目标是最大似然,或者说最小化交叉熵,即
\begin{equation}\mathop{\text{argmin}}_{\theta}\,\mathbb{E}_{(x,y)\sim\mathcal{D}}[-\log p_{\theta}(y|x)]\end{equation}
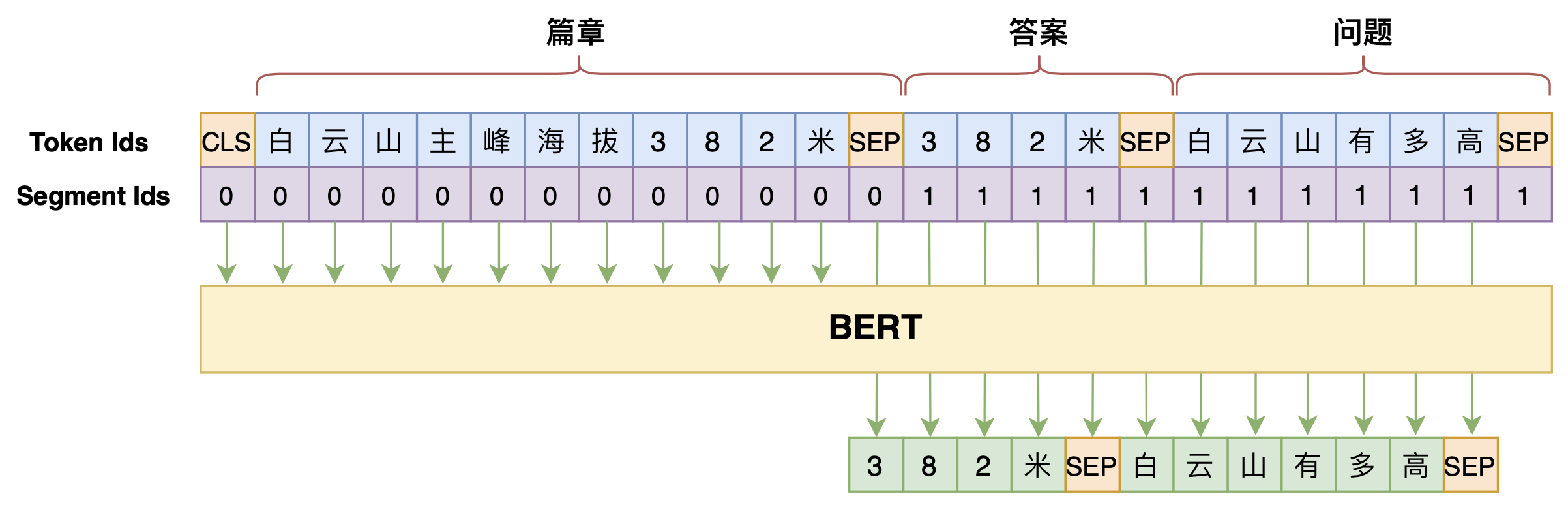
学会提问的BERT:端到端地从篇章中构建问答对
By 苏剑林 | 2020-07-25 | 110976位读者 | 引用机器阅读理解任务,相比不少读者都有所了解了,简单来说就是从给定篇章中寻找给定问题的答案,即“篇章 + 问题 → 答案”这样的流程,笔者之前也写过一些关于阅读理解的文章,比如《基于CNN的阅读理解式问答模型:DGCNN》等。至于问答对构建,则相当于是阅读理解的反任务,即“篇章 → 答案 + 问题”的流程,学术上一般直接叫“问题生成(Question Generation)”,因为大多数情况下,答案可以通过比较规则的随机选择,所以很多文章都只关心“篇章 + 答案 → 问题”这一步。
本文将带来一次全端到端的“篇章 → 答案 + 问题”实践,包括模型介绍以及基于bert4keras的实现代码,欢迎读者尝试。
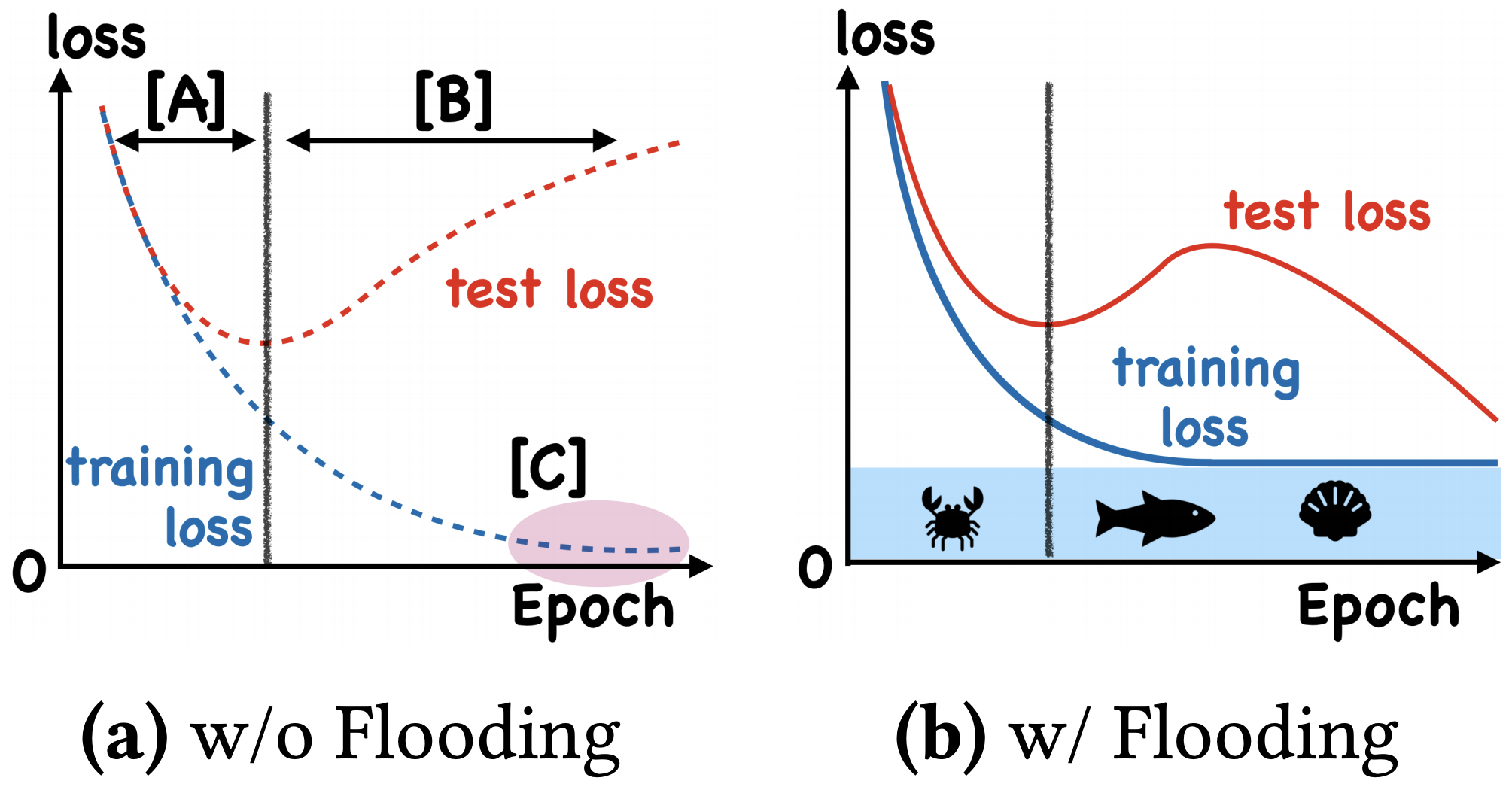
我们真的需要把训练集的损失降低到零吗?
By 苏剑林 | 2020-07-31 | 66242位读者 | 引用在训练模型的时候,我们需要损失函数一直训练到0吗?显然不用。一般来说,我们是用训练集来训练模型,但希望的是验证集的损失越小越好,而正常来说训练集的损失降低到一定值后,验证集的损失就会开始上升,因此没必要把训练集的损失降低到0。
既然如此,在已经达到了某个阈值之后,我们可不可以做点别的事情来提升模型性能呢?ICML 2020的论文《Do We Need Zero Training Loss After Achieving Zero Training Error?》回答了这个问题。不过论文的回答也仅局限在“是什么”这个层面上,并没很好地描述“为什么”,另外看了知乎上kid丶大佬的解读,也没找到自己想要的答案。因此自己分析了一下,记录在此。
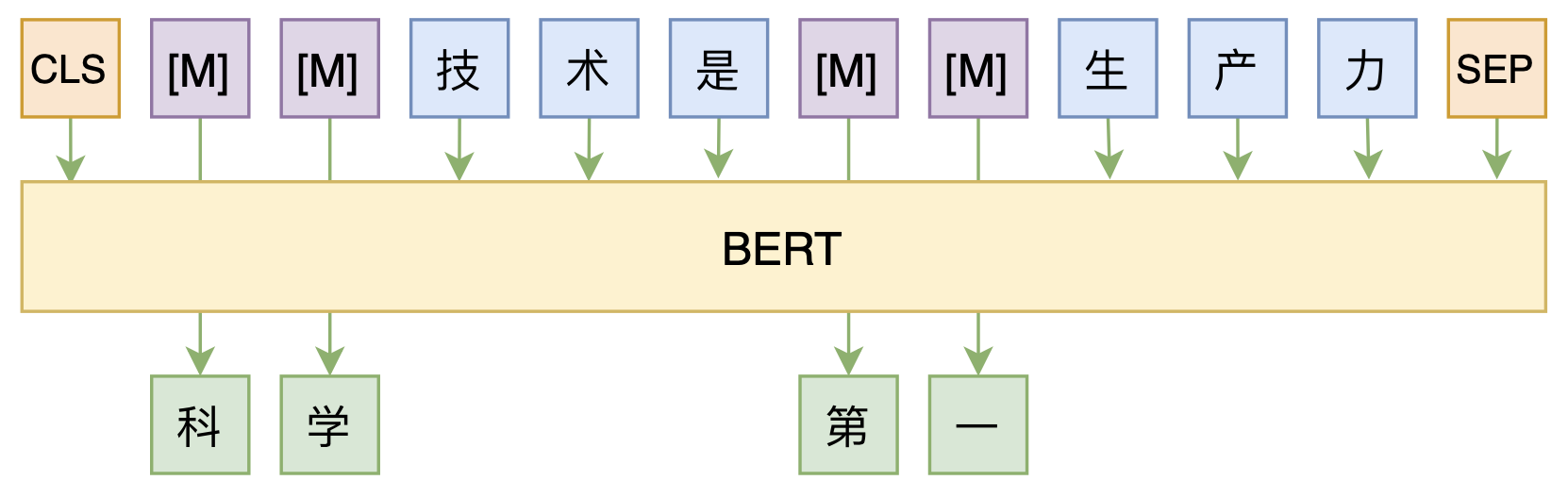
修改Transformer结构,设计一个更快更好的MLM模型
By 苏剑林 | 2020-08-07 | 52833位读者 | 引用大家都知道,MLM(Masked Language Model)是BERT、RoBERTa的预训练方式,顾名思义,就是mask掉原始序列的一些token,然后让模型去预测这些被mask掉的token。随着研究的深入,大家发现MLM不单单可以作为预训练方式,还能有很丰富的应用价值,比如笔者之前就发现直接加载BERT的MLM权重就可以当作UniLM来做Seq2Seq任务(参考这里),又比如发表在ACL 2020的《Spelling Error Correction with Soft-Masked BERT》将MLM模型用于文本纠错。
然而,仔细读过BERT的论文或者亲自尝试过的读者应该都知道,原始的MLM的训练效率是比较低的,因为每次只能mask掉一小部分的token来训练。ACL 2020的论文《Fast and Accurate Deep Bidirectional Language Representations for Unsupervised Learning》也思考了这个问题,并且提出了一种新的MLM模型设计,能够有更高的训练效率和更好的效果。
L2正则没有想象那么好?可能是“权重尺度偏移”惹的祸
By 苏剑林 | 2020-08-14 | 35438位读者 | 引用L2正则是机器学习常用的一种防止过拟合的方法(应该也是一道经常遇到的面试题)。简单来说,它就是希望权重的模长尽可能小一点,从而能抵御的扰动多一点,最终提高模型的泛化性能。但是读者可能也会发现,L2正则的表现通常没有理论上说的那么好,很多时候加了可能还有负作用。最近的一篇文章《Improve Generalization and Robustness of Neural Networks via Weight Scale Shifting Invariant Regularizations》从“权重尺度偏移”这个角度分析了L2正则的弊端,并提出了新的WEISSI正则项。整个分析过程颇有意思,在这里与大家分享一下。
相关内容
这一节中我们先简单回顾一下L2正则,然后介绍它与权重衰减的联系以及与之相关的AdamW优化器。
L2正则的理解
为什么要添加L2正则?这个问题可能有多个答案。有从Ridge回归角度回答的,有从贝叶斯推断角度回答的,这里给出从扰动敏感性的角度的理解。









最近评论