变分自编码器(八):估计样本概率密度
By 苏剑林 | 2021-12-09 | 45110位读者 | 引用在本系列的前面几篇文章中,我们已经从多个角度来理解了VAE,一般来说,用VAE是为了得到一个生成模型,或者是做更好的编码模型,这都是VAE的常规用途。但除了这些常规应用外,还有一些“小众需求”,比如用来估计$x$的概率密度,这在做压缩的时候通常会用到。
本文就从估计概率密度的角度来了解和推导一下VAE模型。
两个问题
所谓估计概率密度,就是在已知样本$x_1,x_2,\cdots,x_N\sim \tilde{p}(x)$的情况下,用一个待定的概率密度簇$q_{\theta}(x)$去拟合这批样本,拟合的目标一般是最小化负对数似然:
\begin{equation}\mathbb{E}_{x\sim \tilde{p}(x)}[-\log q_{\theta}(x)] = -\frac{1}{N}\sum_{i=1}^N \log q_{\theta}(x_i)\label{eq:mle}\end{equation}
VQ-VAE的简明介绍:量子化自编码器
By 苏剑林 | 2019-06-24 | 233116位读者 | 引用印象中很早之前就看到过VQ-VAE,当时对它并没有什么兴趣,而最近有两件事情重新引起了我对它的兴趣。一是VQ-VAE-2实现了能够匹配BigGAN的生成效果(来自机器之心的报道);二是我最近看一篇NLP论文《Unsupervised Paraphrasing without Translation》时发现里边也用到了VQ-VAE。这两件事情表明VQ-VAE应该是一个颇为通用和有意思的模型,所以我决定好好读读它。
EAE:自编码器 + BN + 最大熵 = 生成模型
By 苏剑林 | 2020-04-20 | 41946位读者 | 引用生成模型一直是笔者比较关注的主题,不管是NLP和CV的生成模型都是如此。这篇文章里,我们介绍一个新颖的生成模型,来自论文《Batch norm with entropic regularization turns deterministic autoencoders into generative models》,论文中称之为EAE(Entropic AutoEncoder)。它要做的事情给变分自编码器(VAE)基本一致,最终效果其实也差不多(略优),说它新颖并不是它生成效果有多好,而是思路上的新奇,颇有别致感。此外,借着这个机会,我们还将学习一种统计量的估计方法——$k$邻近方法,这是一种很有用的非参数估计方法。
自编码器vs生成模型
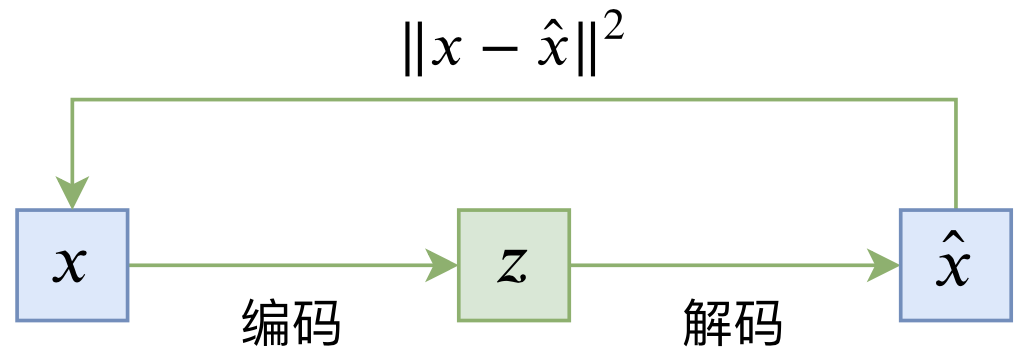
普通的自编码器是一个“编码-解码”的重构过程,如下图所示:
其loss一般为
\begin{equation}L_{AE} = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - \hat{x}\right\Vert^2\right] = \mathbb{E}_{x\sim \tilde{p}(x)}\left[\left\Vert x - D(E(x))\right\Vert^2\right]\end{equation}
从去噪自编码器到生成模型
By 苏剑林 | 2019-10-31 | 85884位读者 | 引用在我看来,几大顶会之中,ICLR的论文通常是最有意思的,因为它们的选题和风格基本上都比较轻松活泼、天马行空,让人有脑洞大开之感。所以,ICLR 2020的投稿论文列表出来之后,我也抽时间粗略过了一下这些论文,确实发现了不少有意思的工作。
其中,我发现了两篇利用去噪自编码器的思想做生成模型的论文,分别是《Learning Generative Models using Denoising Density Estimators》和《Annealed Denoising Score Matching: Learning Energy-Based Models in High-Dimensional Spaces》。由于常规做生成模型的思路我基本都有所了解,所以这种“别具一格”的思路就引起了我的兴趣。细读之下,发现两者的出发点是一致的,但是具体做法又有所不同,最终的落脚点又是一样的,颇有“一题多解”的美妙,遂将这两篇论文放在一起,对比分析一翻。
SVD分解(一):自编码器与人工智能
By 苏剑林 | 2017-01-15 | 40624位读者 | 引用咋看上去,SVD分解是比较传统的数据挖掘手段,自编码器是深度学习中一个比较“先进”的概念,应该没啥交集才对。而本文则要说,如果不考虑激活函数,那么两者将是等价的。进一步的思考就可以发现,不管是SVD还是自编码器,我们降维,并不是纯粹地为了减少储存量或者减少计算量,而是“智能”的初步体现。
等价性
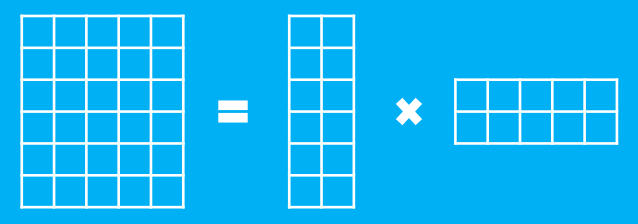
假设有一个$m$行$n$列的庞大矩阵$M_{m\times n}$,这可能使得计算甚至存储上都成问题,于是考虑一个分解,希望找到矩阵$A_{m\times k}$和$B_{k\times n}$,使得
$$M_{m\times n}=A_{m\times k}\times B_{k\times n}$$
这里的乘法是矩阵乘法。如图
用变分推断统一理解生成模型(VAE、GAN、AAE、ALI)
By 苏剑林 | 2018-07-18 | 272595位读者 | 引用前言:我小学开始就喜欢纯数学,后来也喜欢上物理,还学习过一段时间的理论物理,直到本科毕业时,我才慢慢进入机器学习领域。所以,哪怕在机器学习领域中,我的研究习惯还保留着数学和物理的风格:企图从最少的原理出发,理解、推导尽可能多的东西。这篇文章是我这个理念的结果之一,试图以变分推断作为出发点,来统一地理解深度学习中的各种模型,尤其是各种让人眼花缭乱的GAN。本文已经挂到arxiv上,需要读英文原稿的可以移步到《Variational Inference: A Unified Framework of Generative Models and Some Revelations》。
下面是文章的介绍。其实,中文版的信息可能还比英文版要稍微丰富一些,原谅我这蹩脚的英语...
摘要:本文从一种新的视角阐述了变分推断,并证明了EM算法、VAE、GAN、AAE、ALI(BiGAN)都可以作为变分推断的某个特例。其中,论文也表明了标准的GAN的优化目标是不完备的,这可以解释为什么GAN的训练需要谨慎地选择各个超参数。最后,文中给出了一个可以改善这种不完备性的正则项,实验表明该正则项能增强GAN训练的稳定性。
近年来,深度生成模型,尤其是GAN,取得了巨大的成功。现在我们已经可以找到数十个乃至上百个GAN的变种。然而,其中的大部分都是凭着经验改进的,鲜有比较完备的理论指导。
本文的目标是通过变分推断来给这些生成模型建立一个统一的框架。首先,本文先介绍了变分推断的一个新形式,这个新形式其实在博客以前的文章中就已经介绍过,它可以让我们在几行字之内导出变分自编码器(VAE)和EM算法。然后,利用这个新形式,我们能直接导出GAN,并且发现标准GAN的loss实则是不完备的,缺少了一个正则项。如果没有这个正则项,我们就需要谨慎地调整超参数,才能使得模型收敛。
从变分编码、信息瓶颈到正态分布:论遗忘的重要性
By 苏剑林 | 2018-11-27 | 126960位读者 | 引用这是一篇“散文”,我们来谈一下有着千丝万缕联系的三个东西:变分自编码器、信息瓶颈、正态分布。
众所周知,变分自编码器是一个很经典的生成模型,但实际上它有着超越生成模型的含义;而对于信息瓶颈,大家也许相对陌生一些,然而事实上信息瓶颈在去年也热闹了一阵子;至于正态分布,那就不用说了,它几乎跟所有机器学习领域都有或多或少的联系。
那么,当它们三个碰撞在一块时,又有什么样的故事可说呢?它们跟“遗忘”又有什么关系呢?
变分自编码器
在本博客你可以搜索到若干几篇介绍VAE的文章。下面简单回顾一下。
理论形式回顾
简单来说,VAE的优化目标是:
\begin{equation}KL(\tilde{p}(x)p(z|x)\Vert q(z)q(x|z))=\iint \tilde{p}(x)p(z|x)\log \frac{\tilde{p}(x)p(z|x)}{q(x|z)q(z)} dzdx\end{equation}
其中$q(z)$是标准正态分布,$p(z|x),q(x|z)$是条件正态分布,分别对应编码器、解码器。具体细节可以参考《变分自编码器(二):从贝叶斯观点出发》。
漫谈重参数:从正态分布到Gumbel Softmax
By 苏剑林 | 2019-06-10 | 166596位读者 | 引用最近在用VAE处理一些文本问题的时候遇到了对离散形式的后验分布求期望的问题,于是沿着“离散分布 + 重参数”这个思路一直搜索下去,最后搜到了Gumbel Softmax,从对Gumbel Softmax的学习过程中,把重参数的相关内容都捋了一遍,还学到一些梯度估计的新知识,遂记录在此。
文章从连续情形出发开始介绍重参数,主要的例子是正态分布的重参数;然后引入离散分布的重参数,这就涉及到了Gumbel Softmax,包括Gumbel Softmax的一些证明和讨论;最后再讲讲重参数背后的一些故事,这主要跟梯度估计有关。
基本概念
重参数(Reparameterization)实际上是处理如下期望形式的目标函数的一种技巧:
\begin{equation}L_{\theta}=\mathbb{E}_{z\sim p_{\theta}(z)}[f(z)]\label{eq:base}\end{equation}
这样的目标在VAE中会出现,在文本GAN也会出现,在强化学习中也会出现($f(z)$对应于奖励函数),所以深究下去,我们会经常碰到这样的目标函数。取决于$z$的连续性,它对应不同的形式:
\begin{equation}\int p_{\theta}(z) f(z)dz\,\,\,\text{(连续情形)}\qquad\qquad \sum_{z} p_{\theta}(z) f(z)\,\,\,\text{(离散情形)}\end{equation}
当然,离散情况下我们更喜欢将记号$z$换成$y$或者$c$。










最近评论