科学空间|Scientific Spaces

我们知道，梯度累积是在有限显存下实现大batch_size训练的常用技巧。在之前的文章《用时间换取效果：Keras梯度累积优化器》中，我们就简单介绍过梯度累积的实现，大致的思路是新增一组参数来缓存梯度，最后用缓存的梯度来更新模型。美中不足的是，新增一组参数会带来额外的显存占用。

这几天笔者在思考优化器的时候，突然意识到：梯度累积其实可以内置在带动量的优化器中！带着这个思路，笔者对优化了进行了一些推导和实验，最后还得到一个有意思但又有点反直觉的结论：少更新几步参数，模型最终效果可能会变好！

注：本文下面的结果，几乎原封不动且没有引用地出现在Google的论文《Combined Scaling for Zero-shot Transfer Learning》中，在此不做过多评价，请读者自行品评。

SGDM

在正式讨论之前，我们定义函数
\begin{equation}\chi_{t/k} = \left\{ \begin{aligned}&1,\quad t \equiv 0\,(\text{mod}\, k) \\
&0,\quad t \not\equiv 0\,(\text{mod}\, k)
\end{aligned}\right.\end{equation}
也就是说，$t$是一个整数，当它是$k$的倍数时，$\chi_{t/k}=1$，否则$\chi_{t/k}=0$，这其实就是一个$t$能否被$k$整除的示性函数。在后面的讨论中，我们将反复用到这个函数。

点击阅读全文...

前几天在训练一个新的Transformer模型的时候，发现怎么训都不收敛了。经过一番debug，发现是在做Self Attention的时候$\boldsymbol{Q}\boldsymbol{K}^{\top}$之后忘记除以$\sqrt{d}$了，于是重新温习了一下为什么除以$\sqrt{d}$如此重要的原因。当然，Google的T5确实是没有除以$\sqrt{d}$的，但它依然能够正常收敛，那是因为它在初始化策略上做了些调整，所以这个事情还跟初始化有关。

藉着这个机会，本文跟大家一起梳理一下模型的初始化、参数化和标准化等内容，相关讨论将主要以Transformer为心中展开。

采样分布

初始化自然是随机采样的的，所以这里先介绍一下常用的采样分布。一般情况下，我们都是从指定均值和方差的随机分布中进行采样来初始化。其中常用的随机分布有三个：正态分布（Normal）、均匀分布（Uniform）和截尾正态分布（Truncated Normal）。

点击阅读全文...

今天我们来学习Johnson-Lindenstrauss引理，由于名字比较长，下面都简称“JL引理”。

个人认为，JL引理是每一个计算机科学的同学都必须了解的神奇结论之一，它是一个关于降维的著名的结果，它也是高维空间中众多反直觉的“维度灾难”现象的经典例子之一。可以说，JL引理是机器学习中各种降维、Hash等技术的理论基础，此外，在现代机器学习中，JL引理也为我们理解、调试模型维度等相关参数提供了重要的理论支撑。

对数的维度

JL引理，可以非常通俗地表达为：

通俗版JL引理： 塞下$N$个向量，只需要$\mathcal{O}(\log N)$维空间。

点击阅读全文...

这篇文章我们来做一道编程题：

如何在有限内存下全局随机打乱（Shuffle）几百G的文本文件？

题目背景其实很明朗，现在预训练模型动辄就几十甚至几百G语料了，为了让模型能更好地进行预训练，对训练语料进行一次全局的随机打乱是很有必要的。但对于很多人来说，几百G的语料往往比内存还要大，所以如何能在有限内存下做到全局的随机打乱，便是一个很值得研究的问题了。

已有工具

假设我们的文件是按行存储的，也就是一行代表一个样本，我们要做的就是按行随机打乱文件。假设我们只有一个文件，并且这个文件大小明显小于内存，那么我们可以用linux自带的shuf命令：

shuf input.txt -o output.txt

点击阅读全文...

前几天在群里大家讨论到了“Transformer如何解决梯度消失”这个问题，答案有提到残差的，也有提到LN（Layer Norm）的。这些是否都是正确答案呢？事实上这是一个非常有趣而综合的问题，它其实关联到挺多模型细节，比如“BERT为什么要warmup？”、“BERT的初始化标准差为什么是0.02？”、“BERT做MLM预测之前为什么还要多加一层Dense？”，等等。本文就来集中讨论一下这些问题。

梯度消失说的是什么意思？

在文章《也来谈谈RNN的梯度消失/爆炸问题》中，我们曾讨论过RNN的梯度消失问题。事实上，一般模型的梯度消失现象也是类似，它指的是（主要是在模型的初始阶段）越靠近输入的层梯度越小，趋于零甚至等于零，而我们主要用的是基于梯度的优化器，所以梯度消失意味着我们没有很好的信号去调整优化前面的层。

点击阅读全文...

Dropout是经典的防止过拟合的思路了，想必很多读者已经了解过它。有意思的是，最近Dropout有点“老树发新芽”的感觉，出现了一些有趣的新玩法，比如最近引起过热议的SimCSE和R-Drop，尤其是在文章《又是Dropout两次！这次它做到了有监督任务的SOTA》中，我们发现简单的R-Drop甚至能媲美对抗训练，不得不说让人意外。

一般来说，Dropout是被加在每一层的输出中，或者是加在模型参数上，这是Dropout的两个经典用法。不过，最近笔者从论文《Raise a Child in Large Language Model: Towards Effective and Generalizable Fine-tuning》中学到了一种新颖的用法：加到梯度上面。

梯度加上Dropout？相信大部分读者都是没听说过的。那么效果究竟如何呢？让我们来详细看看。

点击阅读全文...

在本博客中，已经多次讨论过梯度惩罚相关内容了。从形式上来看，梯度惩罚项分为两种，一种是关于输入的梯度惩罚$\Vert\nabla_{\boldsymbol{x}} f(\boldsymbol{x};\boldsymbol{\theta})\Vert^2$，在《对抗训练浅谈：意义、方法和思考（附Keras实现）》、《泛化性乱弹：从随机噪声、梯度惩罚到虚拟对抗训练》等文章中我们讨论过，另一种则是关于参数的梯度惩罚$\Vert\nabla_{\boldsymbol{\theta}} f(\boldsymbol{x};\boldsymbol{\theta})\Vert^2$，在《从动力学角度看优化算法（五）：为什么学习率不宜过小？》、《我们真的需要把训练集的损失降低到零吗？》等文章我们讨论过。

在相关文章中，两种梯度惩罚都声称有着提高模型泛化性能的能力，那么两者有没有什么联系呢？笔者从Google最近的一篇论文《The Geometric Occam's Razor Implicit in Deep Learning》学习到了两者的一个不等式，算是部分地回答了这个问题，并且感觉以后可能用得上，在此做个笔记。

最终结果

假设有一个$l$层的MLP模型，记为
\begin{equation}\boldsymbol{h}^{(t+1)} = g^{(t)}(\boldsymbol{W}^{(t)}\boldsymbol{h}^{(t)}+\boldsymbol{b}^{(t)})\end{equation}
其中$g^{(t)}$是当前层的激活函数，$t\in\{1,2,\cdots,l\}$，并记$\boldsymbol{h}^{(1)}$为$\boldsymbol{x}$，即模型的原始输入，为了方便后面的推导，我们记$\boldsymbol{z}^{(t+1)}=\boldsymbol{W}^{(t)}\boldsymbol{h}^{(t)}+\boldsymbol{b}^{(t)}$；参数全体为$\boldsymbol{\theta}=\{\boldsymbol{W}^{(1)},\boldsymbol{b}^{(1)},\boldsymbol{W}^{(2)},\boldsymbol{b}^{(2)},\cdots,\boldsymbol{W}^{(l)},\boldsymbol{b}^{(l)}\}$。设$f$是$\boldsymbol{h}^{(l+1)}$的任意标量函数，那么成立不等式
\begin{equation}\Vert\nabla_{\boldsymbol{x}} f\Vert^2\left(\frac{1 + \Vert \boldsymbol{h}^{(1)}\Vert^2}{\Vert\boldsymbol{W}^{(1)}\Vert^2 \Vert\nabla_{\boldsymbol{x}}\boldsymbol{h}^{(1)}\Vert^2}+\cdots+\frac{1 + \Vert \boldsymbol{h}^{(l)}\Vert^2}{\Vert\boldsymbol{W}^{(l)}\Vert^2 \Vert\nabla_{\boldsymbol{x}}\boldsymbol{h}^{(l)}\Vert^2}\right)\leq \Vert\nabla_{\boldsymbol{\theta}} f\Vert^2\label{eq:f}\end{equation}

点击阅读全文...

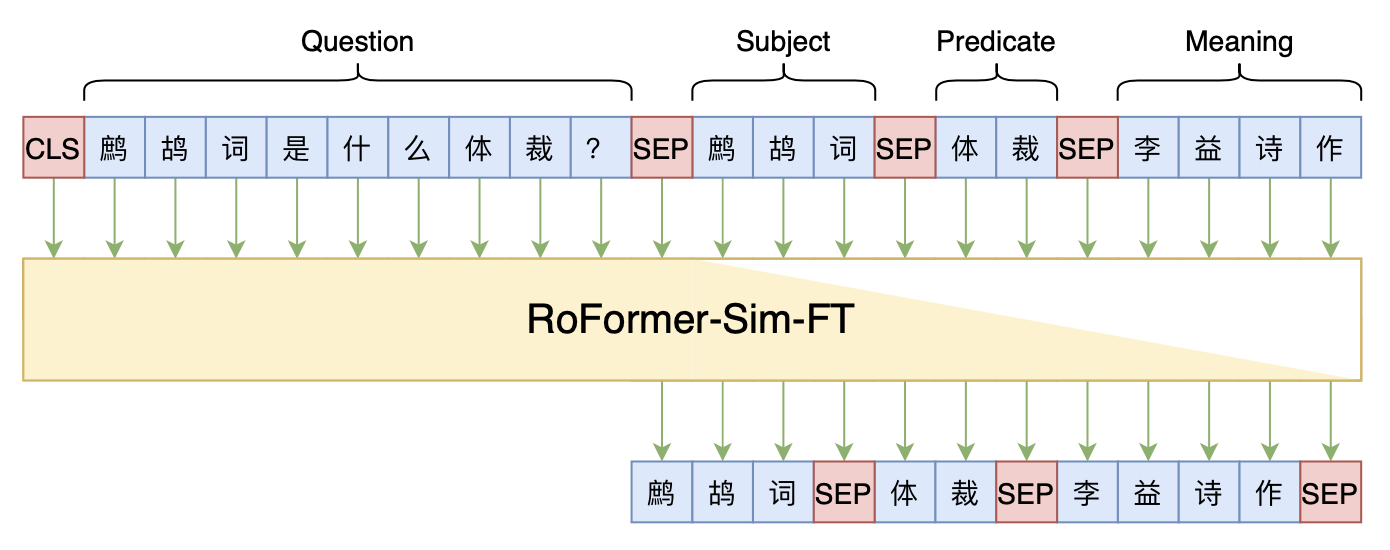
两年前，在《万能的seq2seq：基于seq2seq的阅读理解问答》和《“非自回归”也不差：基于MLM的阅读理解问答》中，我们在尝试过分别利用“Seq2Seq+前缀树”和“MLM+前缀树”的方式做抽取式阅读理解任务，并获得了不错的结果。而在去年的ICLR2021上，Facebook的论文《Autoregressive Entity Retrieval》同样利用“Seq2Seq+前缀树”的组合，在实体链接和文档检索上做到了效果与效率的“双赢”。

事实上，“Seq2Seq+前缀树”的组合理论上可以用到任意检索型任务中，堪称是检索任务的“新范式”。本文将再次回顾“Seq2Seq+前缀树”的思路，并用它来实现最近推出的KgCLUE知识图谱问答榜单的一个baseline。

本文baseline模型示意图

点击阅读全文...