Problem of the Month (August 2004)

This month's problem is to approximate famous mathematical constants using only the first n digits (each used exactly once) and the mathematical symbols + – * / ( ) . and ^. For each n, what is the best approximation you can get to the following constants?

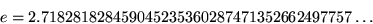
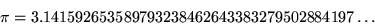
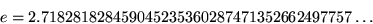
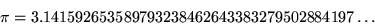
What other constants can you approximate well in this manner?

ANSWERS

Richard Sabey, Joseph DeVincentis, Jeremy Galvagni, Bill Clagett, Bertrand Winter, Berend Jan van der Zwaag, Ambrus Zsbán, and Gerrit de Blaauw sent answers this month, with Richard Sabey and Gerrit de Blaauw furnishing the vast majority of results.

Approximations of γ using 1–n

n	expression	value	error	author
1	1	1.	.42	EF
2	.1^.2	.6	.053	BC
3	3^–1/2	.5773	.00013	EF
4	(4^–.3+.1)²	.57722	1.04E–5	RS
5	(4–3+.1^.5)^–2	.5772153	–2.72E–7	RS
6	(.6^{((.1+.4)^–.3)}–.2)^.5	.577215656	–8.38E–9	GB
7	3^(–.5–2^(–4–.7^(.1–6)))	.577215666	1.21E–9	RS
8	(.4^((6+3*.8)^–7)+.1^.5)^–2	.5772156648	–8.10E–12	RS
9	.8^(.2674^9–1/3)–.5	.5772156648	–4.25E–12	RS

Approximations of e using 1–n

n	expression	value	error	author
1	1	1.	–1.7	EF
2	1+2	3.	.28	EF
3	3–.1–.2	2.70	–.018	EF
4	2^{(.1+.3)^–.4}	2.71829	9.16E–6	RS
5	3^.5+4^–(.1²)	2.718284	1.68E–6	GB
6	((.4+6^.2)*5–1)/3	2.71828180	–2.66E–8	BC
7	2^((.3+.1)^–.4–5^–7.6)	2.718281812	–1.57E–8	RS
8	(1+2^–76)^(4^38+.5)	2.718281828	3.96E–47	RS
9	(1+9^{–4^7*6})^{3^2⁸⁵}	2.718281828	–2.01E–18457734525360901453873570	RS

Approximations of π using 1–n

n	expression	value	error	author
1	1	1.	–2.1	EF
2	1+2	3.0	–.14	EF
3	(1/.3)–.2	3.13	–.0082	BC
4	.4^{–(2.1)^.3}	3.14156	–3.26E–5	GB
5	3+.2/(.4^.1+.5)	3.141598	5.92E–6	BC
6	(4+6/(3^(.2)(.1)))^.5	3.14159263	–1.38E–8	BC
7	3+1/(7+4^{(6^–5–2)})	3.14159269	4.33E–8	RS
8	2^(5^.4)–.6–.1^(38/7)	3.141592654	5.15E–10	RS
9	2^5^.4–.6–(.3^9/7)^(.8^.1)	3.14159265359	6.60E–13	RS

Approximations of Feigenbaum's constant 4.66920160910299 using 1–n

n	expression	value	error	author
1	1	1.	–3.6	RS
2	1/.2	5.	.33	BC
3	(.1)^–2/3	4.64	–.027	RS
4	4*1+2/3	4.666	–.0025	RS
5	(.3^–.1+.4)²/.5	4.66923	2.94E–5	RS
6	(.3^{–(.61^.5)}–.4)²	4.6692017	1.27E–7	GB
7	.2 + (4 + .5^(–13/6))^.7	4.66920161	8.59E–9	GB
8	4+.8^(3*.6)–.2^(7+.1^.5)	4.66920161	1.01E–8	RS
9	4+.8^(2.9)–(76)^–3.15	4.669201608	–3.04E–10	RS

Corey Plover suggested the following variant: use the first n decimal digits of a constant instead of the digits 1 through n. He asks, for a given constant, what is the smallest n that gives a closer approximation than the trivial decimal expansion. Here are some answers.

constant	digits	expression	value	error	author
γ	.57721	(1+(7/.7)^–.5)^–2	.5772153	–2.72E–7	RS
e	2.71	(2–.1)/.7	2.714	–3.99E–3	RS
π	3.141	(.4^.1)/.3+.1	3.1414	–1.14E–4	RS

This got me thinking. What is the best approximation to these constants using ANY n digits? Here's the best known:

Approximations of γ using any digits

	expression	value	error	author
1	.6	.6	.023	AZ
2	3^–.5	.5773	.00013	EF
3	3^–1/2	.5773	.00013	EF
4	(1+.1^.5)^–2	.5772154	–2.72E–7	GB
5	5*.3^(.6^–(.8^–.6))	.5772154	–2.57E–9	GB
6	((6–(.1^(–.7)))/((.1^(–.4))–.8))	.5772156642	–6.27E–10	AZ

Approximations of e using any digits

	expression	value	error	author
1	3	3.	.28	EF
2	2.7	2.70	–.018	EF
3	2^{.4^–.4}	2.71829	9.16E–6	RS
4	(.2+6^.2)/.6	2.71828180	–2.66E–8	GB
5	(1+9^–9)^9⁹	2.718281825	–3.50E–9	RS
6	(1+9^–9)^9⁹+.5	2.718281828	1.50E–18	RS

Approximations of π using any digits

	expression	value	error	author
1	3	3.	–.14	EF
2	.1^–.5	3.16	.026	RS
3	.8^–4+.7	3.1414	–1.86E–4	RS
4	2^{5^.4}–.6	3.141596	3.72E–6	RS
5	.8^–(.1^–.1+5)–.9	3.14159268	3.36E–8	GB
6	((7–(.3^(–.7)))^(.7^(.8^.8)))	3.141592656	–3.14E–9	AZ

Approximations of Feigenbaum's constant 4.66920160910299 using any digits

	expression	value	error	author
1	5	5.	.33	GB
2	9^.7	4.656	–.014	GB
3	6^.86	4.668	3.50E–4	GB
4	9–6^(.8^.9)	4.669198	–3.33E–6	GB
5	(8^.7)^(.6^–.6–.3)	4.669201600	9.50E–10	GB
6	8^((.6^(.1–.7)–.3)*.7)	4.669201600	9.50E–10	GB

And this got Richard Sabey thinking. What is the best approximation to these constants using the digits 1 through n in that order? Here's the best known:

Approximations of γ using 1–n in order

n	expression	value	error	author
1	1	1.	.42	RS
2	.1^.2	.6	.053	RS
3	1.2^–3	.578	.0014	RS
4	(1–2^.3)/–.4	.5778	6.45E–4	RS
5	(1+.2^.3/4)*.5	.5771	–8.64E–5	RS
6	1/(2–.3+.4^.5–.6)	.5772153	–2.72E–7	RS
7	(.1–(23^–.45–.6))^.7	.5772155	–7.13E–8	GB
8	((.1+(2^(3^.4))5.6)^.7)/8	.57721567	1.34E–8	GB
9	.1^–(.2/(.3–4^–(.5^–((6*7)^–.8))–.9))	.5772156644	–5.01E–10	GB

Approximations of e using 1–n in order

n	expression	value	error	author
1	1	1.	–1.7	RS
2	1+2	3.	.28	RS
3	1+2–.3	2.70	–.018	RS
4	.1+2+.3^.4	2.717	–4.80E–4	RS
5	–.1+(–.2+.3)^–.45	2.7183	1.01E–4	RS
6	(1+2)^(.3+.4^5+.6)	2.718284	2.30E–6	RS
7	–((.1–2)/.3^.4–.5+6/7)	2.71828185	2.17E–8	GB
8	((.1^–.2)–((3–.4)^(.5–.6))/.7)^–.8	2.718281825	–2.77E–9	GB
9	(1+2^(–3(4+5)))^(.6.7+8^9)	2.718281826	–1.62E–9	RS

Approximations of π using 1–n in order

n	expression	value	error	author
1	1	1.	–2.1	RS
2	1+2	3.0	–.14	RS
3	.1^(–.2–.3)	3.16	.020	RS
4	(.1+2^.3)^4	3.13	–.0018	RS
5	(.1/.2^.3^4)^–.5	3.1417	1.39E–4	RS
6	.1^(–2/3)+4.5–6	3.14158	–3.81E–6	RS
7	(1+2^–.3)^.4^(–.5/.6^.7)	3.1415924	–1.88E–7	RS
8	.1^(–2/3)+(4/.5)^–6–.7–.8)	3.14159264	–5.28E–9	GB
9	(.1+2^–(3–(4^–((.5+6^–7)^8))))*9	3.14159262	2.43E–8	GB

Approximations of Feigenbaum's constant 4.66920160910299 using 1–n in order

n	expression	value	error	author
1	1	1.	–3.6	RS
2	1/.2	5.	.33	RS
3	(.1)^–2/3	4.64	–.027	RS
4	1*2/3+4	4.666	–.0025	RS
5	.1^.2*(.3–4)/–.5	4.6690	–1.17E–4	RS
6	1/(.2–3^–4)–.5^.6	4.6691	–8.19E–6	RS
7	.12(.3+(4+.5^–.6)7)	4.6692019	3.07E–7	GB
8	.1^–(2/((3/4.5)^(6–.7–8)))	4.669201630	2.04E–8	GB
9	1+2^((3–.4*(.5–.6^7)–.8)^.9)	4.669201613	4.02E–9	GB

Richard Sabey also sent results for expressions without using the decimal point, both in any order and in ascending order. Joseph DeVincentis sent results that use the digits 0–n. And thanks to Berend Jan van der Zwaag for finding a bunch of typos.

In 2008, I extended these results by considering the best approximations to various constants using n copies of a given digit. Here are the best results.

Best Approximations to π with n Copies of the Digit k

n \ k	2	3	4	5	6	7
1	1 + 1 = 2	1 + 1 + 1 = 3	(. 1)^–1/(1+1) = 3.162	1 + (1 + 1)^1.1 = 3.143	.1^-(.1+(.1^.1)/(1+1)) = 3.1416 (GB)	1.1^(11+(1-.1)^-.1) = 3.141598 (GB)
2	2 + 2 = 4	2 + 2^{(. 2)} = 3.149	2^{2^{(. 2)^{(. 2)}}} = 3.144	2 + 2 – 2^{–(. 22)} = 3.1414	2*(.2+.2+2.2^.2) = 3.1416 (GB)	2^(2-.2^-(.2^.2-.2^-.2)) = 3.14158 (GB)
3	3.3 = 3.3	3 + (. 3)/3 = 3.1	3^{3^{3^{(. 3)}}} = 3.140	3 × [(3 – . 3)^{(. 3)} – . 3] = 3.1413	.3^-((3-.3)^-((3-.3)^-3)) = 3.14157 (GB)	3/(.33/(.3-3^-3)-.3) = 3.1415929 (GB)
4	4 – (. 4) = 3.6	4 – (. 4) – (. 4) = 3.2	(. 4)^{–4^{(. 4)×(. 4)}} = 3.139	4 – 4^{–(. 44)/4} = 3.1414	((.4+.4)^-(.4^-(.4^4)))/.4 = 3.141594 (GB)	(4-4/(.4-.4*4^.4))^.4 = 3.141593 (GB)
5	5 × (. 5) = 2.5	(5 + 5)^{(. 5)} = 3.162	5 / [5 × (. 5)]^{(. 5)} = 3.162	5 – (. 5)^{–[5^{–(. 5)}/(. 5)]} = 3.1411	.5+(5^.5)^(.5+.5^.5) = 3.141591 (GB)	.5+.5+.5^-((.5+.5^.5)^.5) = 3.14159268 (GB)
6	6^{(. 6)} = 2.930	6.6^{(. 6)} = 3.103	[6 + (. 6)^{(. 6)}]^{(. 6)} = 3.140	(. 6)^{[6 ×(. 6) –(. 6)^{–(. 6)}]} = 3.142	66.666^6 = 3.1415 (GB)	(6^.6)/(.6^-(6^-(.6/6))-.6) = 3.141593 (GB)
7	7^{(. 7)} = 3.905	7 – 7^{(. 7)} = 3.095	[(. 7)^–7 – 7]^{(. 7)} = 3.147	7^{7/[7+7×(. 7)]} = 3.1413	(77)^((7.7)^-.77) = 3.14158 (GB)	7^-(.7-7^(.7^(7-.7^-.7))) = 3.1415927 (GB)
8	(. 8) + (. 8) = 1.6	(. 8)^{–8^{(. 8)}} = 3.247	(. 8)^{–8×(. 8)×(. 8)} = 3.135	8^{(. 8)} / [(. 8) + (. 88)] = 3.1416	(8/((.8+.8)/.8^.8))^.8 = 3.1416 (GB)	(8^-((.8+.8)^-(8^(.8^.8))))^-8 = 3.1415929 (GB)
9	(. 9)^–9 = 2.581	(. 9)^{–9/(. 9)} = 2.868	9 × (. 9) × (. 9)⁹ = 3.138	(. 9) × [(. 9)^{(. 9)} + (. 9)^–9] = 3.1416	(9-.99.9).9^9 = 3.1415927 (GB)	(.9-.9(.99-9)).9^9 = 3.1415927 (GB)

Best Approximations to e with n Copies of the Digit k

n \ k	2	3	4	5	6	7
1	1 + 1 = 2	1 + 1 + 1 = 3	1 + 1 + (. 1)^{(. 1)} = 2.794	(1 + 1) × [(. 1) + (. 1)^{–(. 1)}] = 2.717	1-.1+(.1+.1)/.11 = 2.7181 (GB)	(1+(.1+.1)^-.1)/(1-.1-.1) = 2.71827 (GB)
2	2 + (. 2) = 2.2	2 + (. 2)^{(. 2)} = 2.725	(. 2)^{[(.2)^{–(. 2)}–2]} = 2.713	2^{[2×(. 2)]^{–2×(. 2)}} = 2.71829	2^(((2^.2)*.2^.2)^-2) = 2.71829 (GB)	2+(2*(2+2^-2))^-.22 = 2.71827 (GB)
3	3 – (. 3) = 2.7	3 × 3 × (. 3) = 2.7	3 × 3^{–(. 3)×(. 3)} = 2.717	[(. 3)^–3 – 3 × 3]^{(. 3)} = 2.7184	(3-.3+.3^-3)^.3-.3 = 2.71827 (GB)	3-.3^(.333+3^-.3) = 2.7182817 (GB)
4	4 – (. 4) = 3.6	4 × (. 4)^{(. 4)} = 2.772	(. 4)^{–[(. 4)+(. 4)^{(. 4)}]} = 2.722	[(4 + 4) / 4]^{(. 4)^{–(. 4)}} = 2.71829	.4+4^(4^-((.4^-.4)/4)) = 2.718287 (GB)	4^((4-.4/4)^-(.4-.4*.4)) = 2.7182815 (GB)
5	5 × (. 5) = 2.5	(. 5) + 5^{(. 5)} = 2.736	55^{(. 5)×(. 5)} = 2.723	5 × (. 55) – (. 5)⁵ = 2.7187	.5^-((5*.5)^(.5-.5/5)) = 2.71829 (GB)	(.5+.5+5^-5)^(.5+5^5) = 2.71828185 (GB)
6	6^{(. 6)} = 2.930	[6 – (. 6)]^{(. 6)} = 2.751	(. 6)^{–(. 6)} + (. 6)^{–(. 6)} = 2.717	(. 6)^{–[(. 6)×6^{(. 66)}]} = 2.7183	(6/6+6^-6)^(6^6) = 2.71825 (GB)	(.6+.6+6^(.6+.6))/(6*.6) = 2.71828180 (GB)
7	7^{(. 7)} = 3.905	(. 7) / 7^{–(. 7)} = 2.733	7.7^{(. 7)×(. 7)} = 2.7188	7^{[(. 77)–7^{–(. 7)}]} = 2.71822	.7^-((7+7*7)^(7^-.7)) = 2.7183 (GB)	(.7^-((7+7)^(7^-.77)))/.7 = 2.7182817 (GB)
8	(. 8) + (. 8) = 1.6	8 – 8^{(. 8)} = 2.722	(. 8)^{[(. 8)–8^{(. 8)}]} = 2.716	(. 8) + 8 × (. 8)^{8×(. 8)} = 2.7180	.8(.8+.8^-8)^(.8.8) = 2.7181 (GB)	(8/(8-8^-8))^(8/8^-8) = 2.71828183 (GB)
9	(. 9)^–9 = 2.581	(. 9) + (. 9) + (. 9) = 2.7	9^{–(. 9)} + (. 9)^–9 = 2.719	(. 9) + (. 9) + (. 9)^{(. 9)×(. 9)} = 2.7181	9*(.9+.9)-(9+9)^.9 = 2.7182815 (GB)	(.9/(.9+9^-9))^-(.9/9^-9) = 2.718281824 (GB)

Best Approximations to γ with n Copies of the Digit k

n \ k	2	3	4	5	6	7
1	(. 1)^{(. 1)} = .794	[(. 1) × (. 1)]^{(. 1)} = .630	(1 + 1)^{–(. 1)^{(. 1)}} = .576	(. 1) / (. 11)^{(. 1)^{(. 1)}} = .5773	.1*((.1+.1)^-1.1-.1) = .5773 (GB)	(1+.1^(1/(1+1)))^-(1+1) = .57723 (GB)
2	(. 2)^{(. 2)} = .724	2^{(. 2)} / 2 = .574	2 – (. 2)^{–(. 22)} = .575	[(. 2) / (2 – (. 2))]^{2^–2} = .5773	.2+.2^(.2^(.2^(.2^.2))) = .577218 (GB)	2^-((.2^-.2-.2^-(.2^2))^.2) = .5772151 (GB)
3	(. 3) + (. 3) = .6	(3 + 3)^{–(. 3)} = .584	3^–3/[3+3] = .5773	(. 3)^{–(. 3)} – [(. 3) + (. 3)]^{(. 3)} = .5771	3*(.3^(.3^.3))-3^-.3 = .57722 (GB)	.3/.3^((3+(.3+.3)^-3)^-.3) = .5772157 (GB)
4	4^{–(. 4)} = .574	(. 4) / (. 4)^{(. 4)} = .5770	(. 4)^{4×(. 4)} / (. 4) = .5770	[(. 4)^{(. 4)} – (. 44)]^{(. 4)} = .57722	.4*(.4+(4/(4-.4))^.4) = .577217 (GB)	(44+4)^-((4-.4)^-4)-.4 = .5772154 (GB)
5	(. 55) = .55	(. 555) = .555	[5 × (. 5) + (. 5)]^{&ndash(. 5)} = .5773	(. 5) / (. 5)^{[(. 5)^{(. 5)}–(. 5)]} = .5771	.5^(.5+(.5^-.55)/5) = .5772158 (GB)	.5/(.5+5^-((5^(.5^.5))/5)) = .5772158 (GB)
6	(. 66) = .66	6^{–(. 6)} / (. 6) = .569	[6 / 6 – (. 6)]^{(. 6)} = .5770	[6^{6^–6} – (. 6)]^{(. 6)} = .5771	.6-(6^.6)*((.6^6)/6) = .5772151 (GB)	(.6+(6-(.6^-.6)/6)^.6)/6 = .5772158 (GB)
7	(. 7) × (. 7) = .49	7 × 7^{(. 7)} = .576	[(. 7) × (. 7)]^{(. 77)} = .5773	(. 7) – [(. 7) / (7 + 7)]^{(. 7)} = .5771	(.7^(.7*(.7+.7)))^-.7-.7 = .577211 (GB)	.7-((7-.7)^-(7^-(.7^-.7)))/7 = .5772158 (GB)
8	(. 8) × (. 8) = .64	(. 8) – 8^{–(. 8)} = .610	8^{–8^{–(. 8)×(. 8)}} = .57723	[(. 8) × (. 8)]^{8^{(. 8)/8}} = .57727	(.8*8^(.8^8.8))^-8 = .577216 (GB)	((8^-((.8^8)*(.8^.8)))/.8)^8 = .577216 (GB)
9	(. 9)⁹ = .387	[(. 9) + (. 9)]^{–(. 9)} = .589	[(. 9) × (. 9)]^{(. 9)^–9} = .580	[(. 9) + 9^{–(. 9)}] / [(. 9) + (. 9)] = .576	(9^(.9-.9^(9+9)))/9 = .57723 (GB)	(9-.9/9)/(9+9-.9^-9) = .577216 (GB)

Best Approximations to Feigenbaum's Constant with n Copies of the Digit k

n \ k	2	3	4	5	6	7
1	1 + 1 = 2	1 / [(. 1) + (. 1)] = 5	1 / [(. 11) + (. 1)] = 4.762	(1 + 1)^–1.1 / (. 1) = 4.665	.1^-((.1^.1-.1)^1.1) = 4.67 (GB)	.1+.1+1/(1-.1^.11) = 4.66921 (GB)
2	2 + 2 = 4	2^2.2 = 4.594	2^{–(. 2)/2} / (. 2) = 4.665	2 + 2 + (. 2)^{2^–2} = 4.668	.2+(2*2^.2)^(2-.2) = 4.6691 (GB)	.2^-(.2^(2^-(2+.2^-(.2^.2)))) = 4.669203 (GB)
3	3 + 3 = 6	3^{(. 3)} / (. 3) = 4.634	(. 33)^{–3^{(. 3)}} = 4.671	3^{[3 + (. 3) × (. 3)]^{(. 3)}} = 4.6697	3*(.3+.3+.3^(3^-3)) = 4.6691 (GB)	.3^-((.3+.3)^(.3^3))+3^.3 = 4.6692014 (GB)
4	4 + (. 4) = 4.4	4 + (. 4)^{(. 4)} = 4.693	4 + (. 4)^{(. 44)} = 4.668	4 / [(. 4) + (. 4)]^{(. 4)^{(. 4)}} = 4.6690	4+.4^(.4/(.4^(.4/4))) = 4.6691 (GB)	.44-(4/.4^.4-4/.4) = 4.669200 (GB)
5	5 – (. 5) = 4.5	(. 5)^{–5^{(. 5)}} = 4.711	5 × (. 5)^{(. 5)/5} = 4.665	[5 – (. 5)^{–(. 5)^{–(. 5)}}] / (. 5) = 4.6697	5-(5^-(.5*5^.5))/.5 = 4.669205 (GB)	.5^5+5.5^((5-.5)/5) = 4.669203 (GB)
6	6 – (. 6) = 5.4	6 – (. 6)^{–(. 6)} = 4.641	6 – (. 6) – (. 6)^{(. 6)} = 4.663	6 – 6^{(. 6)^6×(.6)} = 4.670	6^(6/(6+.6^(.6^6))) = 4.6691 (GB)	6*(.6^((6-.6)/66))^6 = 4.66921 (GB)
7	7 × (. 7) = 4.9	(. 7) + 7^{(. 7)} = 4.604	(. 77) + 7^{(. 7)} = 4.674	(. 7) × [7 – (7×(. 7))^{–(. 7)}] = 4.6698	7^(.7^(.7^(.7+.7*.7))) = 4.6691 (GB)	((.77+.7^.7)/(7+7))^-.7 = 4.6692019 (GB)
8	8^{(. 8)} = 5.278	(. 8) / (. 8)⁸ = 4.768	(. 88) / 8^{–(. 8)} = 4.644	[8 / (. 8)]^{(. 8)×(. 8)^{(. 8)}} = 4.668	.8*(8/(.8+.8)+.8^.8) = 4.669209 (GB)	8/(8^.8-.8^-(8.8^.8)) = 4.6691 (GB)
9	(. 9)^–9 = 2.581	9 / [(. 9) + (. 9)] = 5	[(. 9) + (. 9)] / 9^{(. 9)} = 4.646	(. 9) + (. 9) + (. 9)^–9 / (. 9) = 4.667	9^.9-.99*.9^-9 = 4.6693 (GB)	.9/(.99+.9-(.9+.9)^.9) = 4.669207 (GB)

If you can extend any of these results, please e-mail me. Click here to go back to Math Magic. Last updated 5/15/08.