多任务学习漫谈（三）：分主次之序

多任务学习是一个很宽泛的命题，不同场景下多任务学习的目标不尽相同。在《多任务学习漫谈（一）：以损失之名》和《多任务学习漫谈（二）：行梯度之事》中，我们将多任务学习的目标理解为“做好每一个任务”，具体表现是“尽量平等地处理每一个任务”，我们可以称之为“平行型多任务学习”。然而，并不是所有多任务学习的目标都是如此，在很多场景下，我们主要还是想学好某一个主任务，其余任务都只是辅助，希望通过增加其他任务的学习来提升主任务的效果罢了，此类场景我们可以称为“主次型多任务学习”。

在这个背景下，如果还是沿用平行型多任务学习的“做好每一个任务”的学习方案，那么就可能会明显降低主任务的效果了。所以本文继续沿着“行梯度之事”的想法，探索主次型多任务学习的训练方案。

目标形式 #

在这篇文章中，我们假设读者已经阅读并且基本理解《多任务学习漫谈（二）：行梯度之事》里边的思想和方法，那么在梯度视角下，让某个损失函数保持下降的必要条件是更新量与其梯度夹角至少大于90度，这是贯穿全文的设计思想。

约束优化 #

现在假设主次型多任务学习场景下，我们有$n+1$个任务的损失函数，分别为$\mathcal{L}_0,\mathcal{L}_1,\cdots,\mathcal{L}_n$，其中$\mathcal{L}_0$是主任务损失，我们希望它越小越好；而$\mathcal{L}_1,\cdots,\mathcal{L}_n$是辅助损失，相当于正则项，我们只希望它在训练过程中不要往上升的方向走，但不一定要“拼了命地变小”。

沿用《多任务学习漫谈（二）：行梯度之事》的记号，我们记每一步的更新量为$\Delta\boldsymbol{\theta}=-\eta\boldsymbol{u}$，既然我们以$\mathcal{L}_0$为主任务，那么自然希望最大化$\boldsymbol{u}$与$\boldsymbol{g}_0$的内积，可以设计优化目标为
\begin{equation}\max_{\boldsymbol{u}} \langle\boldsymbol{u},\boldsymbol{g}_0\rangle - \frac{1}{2}\Vert\boldsymbol{u}\Vert^2\end{equation}
这里$\boldsymbol{g}_i = \nabla_{\boldsymbol{\theta}}\mathcal{L}_i$是对应损失的梯度。如果没有其他约束，那么将会解得$\boldsymbol{u} = \boldsymbol{g}_0$，这就是普通的梯度下降。但事实上我们还有辅助任务$\mathcal{L}_1,\cdots,\mathcal{L}_n$，我们希望它们不要往上升的方向走，所以至少还要保证$\langle\boldsymbol{u},\boldsymbol{g}_1\rangle\geq 0,\cdots,\langle\boldsymbol{u},\boldsymbol{g}_n\rangle\geq 0$，它们是优化的约束条件，从而总的目标是
\begin{equation}\max_{\boldsymbol{u}} \langle\boldsymbol{u},\boldsymbol{g}_0\rangle - \frac{1}{2}\Vert\boldsymbol{u}\Vert^2\quad\text{s.t.}\,\, \langle\boldsymbol{u},\boldsymbol{g}_1\rangle\geq 0,\cdots,\langle\boldsymbol{u},\boldsymbol{g}_n\rangle\geq 0\end{equation}
求解这个约束优化问题，就可以得到满足条件的更新量。

拉氏乘子 #

求解这种带约束优化问题的标准方案是拉格朗日乘子法，简称“拉氏乘子”，它将约束条件整合到目标函数中，转化为一个min-max问题：
\begin{equation}\max_{\boldsymbol{u}} \min_{\lambda_i\geq 0}\langle\boldsymbol{u},\boldsymbol{g}_0\rangle - \frac{1}{2}\Vert\boldsymbol{u}\Vert^2 + \sum_i \lambda_i \langle\boldsymbol{u},\boldsymbol{g}_i\rangle\label{eq:q-1}\end{equation}

这里约定对$i$的求和是从$1$到$n$。怎么理解这个转换呢？假如$\langle\boldsymbol{u},\boldsymbol{g}_i\rangle > 0$，那么$\min\limits_{\lambda_i\geq 0}$这一步就只能得到$\lambda_i=0$，因为只有$\lambda_i=0$能使得它取最小，此时$\lambda_i \langle\boldsymbol{u},\boldsymbol{g}_i\rangle=0$；如果$\langle\boldsymbol{u},\boldsymbol{g}_i\rangle=0$，那么自然地$\lambda_i \langle\boldsymbol{u},\boldsymbol{g}_i\rangle=0$；如果$\langle\boldsymbol{u},\boldsymbol{g}_i\rangle < 0$，那么$\min\limits_{\lambda_i\geq 0}$这一步就会得到$\lambda_i\to\infty$，此时$\lambda_i \langle\boldsymbol{u},\boldsymbol{g}_i\rangle\to -\infty$。但是别忘了，$\boldsymbol{u}$的优化是取$\max$的，所以在$0$与$-\infty$之间，它自然会选择$0$，也就是完成该min-max优化后，必然自动地有$\langle\boldsymbol{u},\boldsymbol{g}_i\rangle \geq 0$以及$\lambda_i \langle\boldsymbol{u},\boldsymbol{g}_i\rangle=0$。这意味着min-max的优化结果跟原来带约束的max优化完全等价。

为了方便后面的推导，这里引入跟上一篇文章类似的记号：
\begin{equation}\mathbb{Q}^n=\left\{(\lambda_1,\cdots,\lambda_n)\left|\lambda_1,\cdots,\lambda_n\geq 0\right.\right\},\quad\tilde{\boldsymbol{g}}(\lambda) = \sum_i \lambda_i \boldsymbol{g}_i\end{equation}
那么式$\eqref{eq:q-1}$可以记为
\begin{equation}\max_{\boldsymbol{u}} \min_{\lambda\in\mathbb{Q}^n}\langle\boldsymbol{u},\boldsymbol{g}_0 + \tilde{\boldsymbol{g}}(\lambda)\rangle - \frac{1}{2}\Vert\boldsymbol{u}\Vert^2\label{eq:q-2}\end{equation}

求解算法 #

至此，我们将主次型多任务学习的更新方向求解转化为了一个min-max问题$\eqref{eq:q-2}$。接下来，跟上一篇文章的方式类似，我们先通过Minimax定理来交换$\max$和$\min$的次序，然后进一步通过Frank-Wolfe算法给出求解方式，最后我们会比较它跟它跟上一篇文章结果的异同。

交换次序 #

注意到问题$\eqref{eq:q-2}$的$\max$和$\min$是有次序的，正常来说必须要先完成$\min$这一步后才能再做$\max$这一步，贸然交换次序可能会得到错误的结果。然而，$\min$这一步是有约束的优化，而$\max$这一步是无约束的，因此相对来说$\max$确实简单一些。如果我们能交换次序，先进行$\max$这一步，那么问题就可以得到简化。

所以，我们需要先判断两者的次序能否交换。幸运的是，冯·诺依曼提出了美妙的Minimax定理，它告诉我们如果$\min$和$\max$的参数可行域都是一个凸集，并且目标函数关于$\min$的参数是凸的、关于$\max$的参数是凹的，那么$\min$和$\max$的次序就可以交换。更幸运的是，容易看出问题$\eqref{eq:q-2}$满足Minimax定理的条件，从而它等价于
\begin{equation}\min_{\lambda\in\mathbb{Q}^n}\max_{\boldsymbol{u}} \langle\boldsymbol{u},\boldsymbol{g}_0 + \tilde{\boldsymbol{g}}(\lambda)\rangle - \frac{1}{2}\Vert\boldsymbol{u}\Vert^2 =\min_{\lambda\in\mathbb{Q}^n}\frac{1}{2}\Vert\boldsymbol{g}_0 + \tilde{\boldsymbol{g}}(\lambda)\Vert^2\label{eq:q-3}\end{equation}
这样我们就将问题简化为只有$\min$操作了，其中等号右边是因为左边的目标函数只是关于$\boldsymbol{u}$的二次函数，它的最大值在$\boldsymbol{u}^* = \boldsymbol{g}_0 + \tilde{\boldsymbol{g}}(\lambda)$取到，代入即得等号右边结果。

简单情形 #

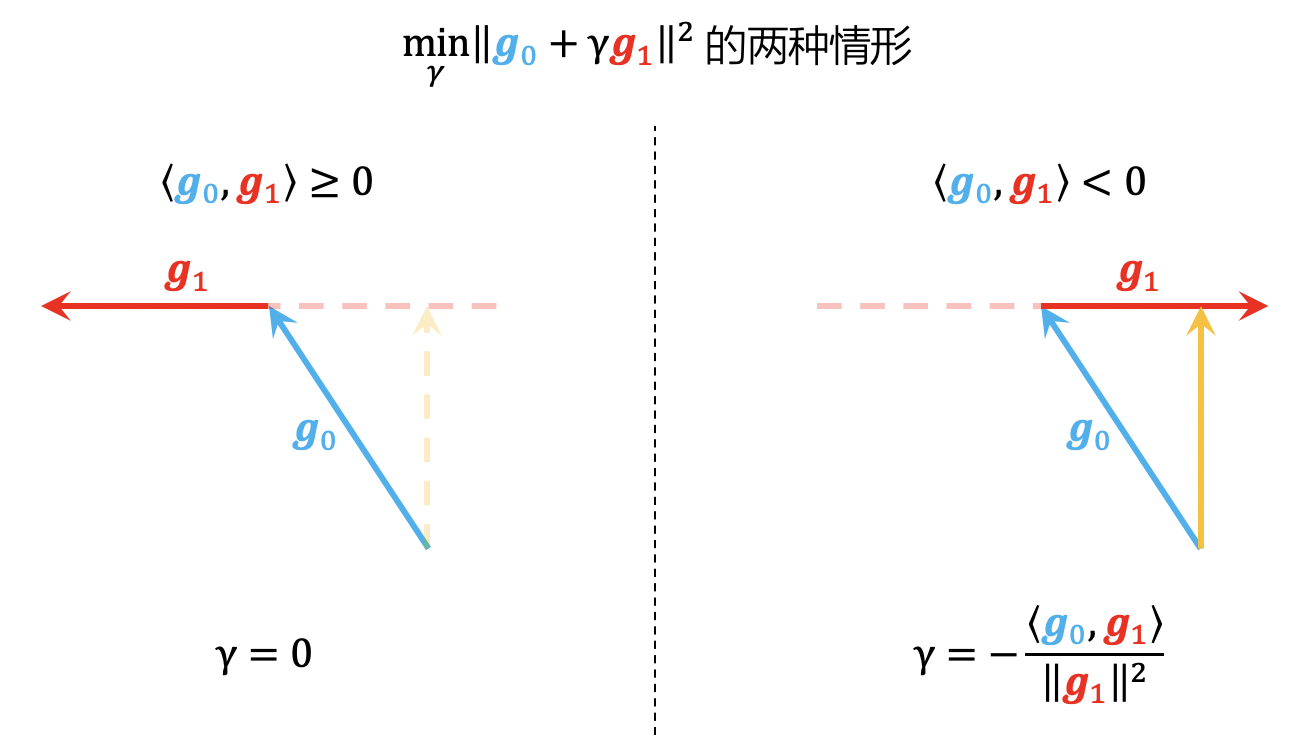
现在问题变成了求$\boldsymbol{g}_0$与$\boldsymbol{g}_1,\cdots,\boldsymbol{g}_n$的最小模长的加权叠加。按照惯例，我们先试着解决最简单的情形，即$n=1$时的$\min\limits_{\gamma\geq 0}\Vert\boldsymbol{g}_0 + \gamma\boldsymbol{g}_1\Vert^2$，它有着形象的几何意义和简单的解析解。

如上图所示，共有两种情形：第一种情形是$\langle\boldsymbol{g}_0,\boldsymbol{g}_1\rangle\geq 0$，这说明$\boldsymbol{g}_0$与$\boldsymbol{g}_1$本就不冲突，所以直接取$\gamma=0$就行；第二种情形是$\langle\boldsymbol{g}_0,\boldsymbol{g}_1\rangle < 0$，从上面右图可以看出，$\Vert\boldsymbol{g}_0 + \gamma\boldsymbol{g}_1\Vert^2$的最小值在$\boldsymbol{g}_0 + \gamma\boldsymbol{g}_1$与$\boldsymbol{g}_1$垂直时取到，于是由$\langle \boldsymbol{g}_0 + \gamma\boldsymbol{g}_1,\boldsymbol{g}_1\rangle=0$解得$\gamma = -\frac{\langle \boldsymbol{g}_0,\boldsymbol{g}_1\rangle}{\Vert\boldsymbol{g}_1\Vert^2}$。最后，当$\Vert\boldsymbol{g}_1\Vert\neq 0$时，也可以统一写成
\begin{equation}\gamma = \frac{\text{relu}(-\langle \boldsymbol{g}_0,\boldsymbol{g}_1\rangle)}{\Vert\boldsymbol{g}_1\Vert^2}\label{eq:gamma}\end{equation}

迭代求解 #

接下来我们处理一般情形，其思想依然源自Frank-Wolfe算法。

首先，我们通过$\tau = \mathop{\arg\min}\limits_i \langle \boldsymbol{g}_i, \boldsymbol{g}_0 + \tilde{\boldsymbol{g}}(\lambda^{(k)})\rangle$找出下一步更新的可行方向$e_{\tau}$。接着，我们进行一维搜索，但跟之前不同的是，这次不是在$\lambda^{(k)}$与$e_{\tau}$之间插值搜索，而是直接重新确定$\boldsymbol{g}_{\tau}$对应的系数，也就是说，我们直接在$\tilde{\boldsymbol{g}}(\lambda^{(k)})$中把$\boldsymbol{g}_{\tau}$部分删掉，然后重新用$n=1$情形的算法重新计算$\boldsymbol{g}_{\tau}$对应的系数。

由此，我们得到下述迭代过程：
\begin{equation}\left\{\begin{aligned}
&\tau = \mathop{\arg\min}_i \langle \boldsymbol{g}_i, \boldsymbol{g}_0+\tilde{\boldsymbol{g}}(\lambda^{(k)})\rangle\\
&\gamma = \mathop{\arg\min}_{\gamma} \left\Vert\boldsymbol{g}_0 + \tilde{\boldsymbol{g}}(\lambda^{(k)} - \lambda^{(k)}_{\tau} e_{\tau} + \gamma e_{\tau})\right\Vert^2 = \mathop{\arg\min}_{\gamma} \left\Vert\boldsymbol{g}_0 + \tilde{\boldsymbol{g}}(\lambda^{(k)}) - \lambda^{(k)}_{\tau}\boldsymbol{g}_{\tau} + \gamma \boldsymbol{g}_{\tau}\right\Vert^2\\
&\lambda^{(k+1)} = \lambda^{(k)} - \lambda^{(k)}_{\tau} e_{\tau} + \gamma e_{\tau}
\end{aligned}\right.\end{equation}

两相比较 #

至此，我们完成了本文所探究的主次型多任务学习的求解。对于认真推导过两篇文章的数学结果的同学来说，定然会感觉到平行型和主次型的方法和结果都非常相似。事实上确实如此，它们有诸多相似之处，但细微之处又有不同。

为了加深大家的理解，我们可以将这两种多任务学习的异同对比如下：
$$\small
\begin{array}{c|c|c}
\hline
& \text{平行型多任务学习(前文)} & \text{主次型多任务学习(本文)} \\
\hline
\text{目标概述} & \text{学好每一个任务} & \text{学好主任务，但不让辅任务变差} \\
\hline
\text{增量格式} & \Delta\boldsymbol{\theta} = -\eta\boldsymbol{u} & \Delta\boldsymbol{\theta} = -\eta\boldsymbol{u} \\
\hline
\text{数学定义} & \max\limits_{\boldsymbol{u}}\min\limits_i \langle \boldsymbol{g}_i, \boldsymbol{u}\rangle - \frac{1}{2}\Vert \boldsymbol{u}\Vert^2 & {\begin{array}{l}\max\limits_{\boldsymbol{u}} \langle\boldsymbol{u},\boldsymbol{g}_0\rangle - \frac{1}{2}\Vert\boldsymbol{u}\Vert^2 \\ \text{s.t.}\,\, \langle\boldsymbol{u},\boldsymbol{g}_1\rangle\geq 0,\cdots,\langle\boldsymbol{u},\boldsymbol{g}_n\rangle\geq 0\end{array}} \\
\hline
\text{对偶结果} & \min\limits_{\alpha\in\mathbb{P}^n}^{\,^\,}\Vert\tilde{\boldsymbol{g}}(\alpha)\Vert^2 & \min\limits_{\lambda\in\mathbb{Q}^n}\Vert\boldsymbol{g}_0 + \tilde{\boldsymbol{g}}(\lambda)\Vert^2 \\
\hline
\text{方向向量} & \boldsymbol{u}=\tilde{\boldsymbol{g}}(\alpha)=\sum\limits_i^{\,^\,} \alpha_i \boldsymbol{g}_i & \boldsymbol{u}=\boldsymbol{g}_0+\tilde{\boldsymbol{g}}(\lambda)=\boldsymbol{g}_0 + \sum\limits_i \lambda_i \boldsymbol{g}_i \\
\hline
\text{可行空间} & \mathbb{P}^n = \left\{(\alpha_1,\cdots,\alpha_n)\left|\forall\alpha_i\geq 0, \sum\limits_i \alpha_i = 1\right.\right\} & \mathbb{Q}^n=\left\{(\lambda_1,\cdots,\lambda_n)\left|\forall\lambda_i\geq 0\right.\right\} \\
\hline
\text{迭代步骤} & \left\{\begin{aligned}
&\tau = \mathop{\arg\min}_i \langle \boldsymbol{g}_i, \tilde{\boldsymbol{g}}(\alpha^{(k)})\rangle\\
&\gamma = \mathop{\arg\min}_{\gamma} \left\Vert(1-\gamma)\tilde{\boldsymbol{g}}(\alpha^{(k)}) + \gamma \boldsymbol{g}_{\tau}\right\Vert^2\\
&\alpha^{(k+1)} = (1-\gamma)\alpha^{(k)} + \gamma e_{\tau}
\end{aligned}\right. & \left\{\begin{aligned}
&\tau = \mathop{\arg\min}_i \langle \boldsymbol{g}_i, \boldsymbol{g}_0+\tilde{\boldsymbol{g}}(\lambda^{(k)})\rangle\\
&\gamma = \mathop{\arg\min}_{\gamma} \left\Vert\boldsymbol{g}_0 + \tilde{\boldsymbol{g}}(\lambda^{(k)}) - \lambda^{(k)}_{\tau}\boldsymbol{g}_{\tau} + \gamma \boldsymbol{g}_{\tau}\right\Vert^2\\
&\lambda^{(k+1)} = \lambda^{(k)} - \lambda^{(k)}_{\tau} e_{\tau} + \gamma e_{\tau}
\end{aligned}\right. \\
\hline
\end{array}$$

经过这样对比，我们也不难将结果推广到有$n$个主任务、$m$个辅任务的混合型多任务学习，其对偶结果是：
\begin{equation}\min_{\alpha\in\mathbb{P}^n,\lambda\in\mathbb{Q}^m}\Vert\tilde{\boldsymbol{g}}(\alpha) + \tilde{\boldsymbol{g}}(\lambda)\Vert^2\end{equation}
至于具体的迭代算法，请大家自行思考～

应用思考 #

在这一节中，我们通过几个例子说明，很多常见的问题都可以对应到这种有主次之分的多任务学习中，某种意义上来说，主次型多任务学习可能比平行型多任务学习更为常见。

正则损失 #

最常见的例子可能是往任务损失函数里边加入的正则项，比如L2正则：
\begin{equation}\mathcal{L}(\boldsymbol{\theta}) + \frac{\lambda}{2}\Vert\boldsymbol{\theta}\Vert^2\end{equation}
如果我们将$\mathcal{L}(\boldsymbol{\theta})$和$\frac{1}{2}\Vert\boldsymbol{\theta}\Vert^2$看成是两个任务的损失，那么这也可以视为一个多任务学习问题。很显然，我们并没有想要$\frac{1}{2}\Vert\boldsymbol{\theta}\Vert^2$越小越好，而只是希望$\frac{1}{2}\Vert\boldsymbol{\theta}\Vert^2$的加入能够提高$\mathcal{L}(\boldsymbol{\theta})$的泛化性能，所以这就无法对应上平行型多任务学习，而更贴近主次型多任务学习了。

L2正则项$\frac{1}{2}\Vert\boldsymbol{\theta}\Vert^2$的梯度比较简单，就是$\boldsymbol{\theta}$。那么，套用本文的结果$\eqref{eq:gamma}$，我们可以修改优化器，将梯度项改为
\begin{equation}\boldsymbol{g} + \frac{\text{relu}(-\langle \boldsymbol{g},\boldsymbol{\theta}\rangle)}{\Vert\boldsymbol{\theta}\Vert^2}\end{equation}
这样就可以实现往模型里边加入L2正则但又不用调正则项系数$\lambda$了。当然，也可以像AdamW那样直接对原本的更新量进行处理，实现解耦形式的权重衰减（Decoupled Weight Decay）。

当然，除了这种对参数的直接正则外，还有很多其他形式的辅助损失，比如有往分类模型加入对比学习损失的、有往生成模型加入长度惩罚的，等等。这些做法多多少少都可以对应上主次型多任务学习中，因此可以尝试套用本文的结果。如果觉得完整梯度的计算量较大，那么也可以跟上一篇文章一样，对“共享编码”的情形进行近似来降低计算量。

带噪学习 #

此外，有一种常见的训练场景，大家可能没意识到它是一个多任务学习问题，但它本质上确实也可以视为多任务学习问题来理解，那就是“带噪学习”。

假设对于同一种任务，我们只有少量精标的干净数据，但同时有大量的噪声数据。由于噪声数据较多，所以我们倾向于以噪声数据为主进行学习，假设对应的损失为$\mathcal{L}_0$。然而，由于数据中存在噪声，因此纯粹最小化$\mathcal{L}_0$未必能得到理想的模型，它可能把错误的标注也背下来了。这时，干净数据就可以派上用场了，我们可以用干净数据算一个损失$\mathcal{L}_1$。由于干净数据的噪声较少，可以认为$\mathcal{L}_1$比$\mathcal{L}_0$更能反映模型的真实性能，那么我们就可以增加一个限制：

不管怎么最小化$\mathcal{L}_0$，都不能让$\mathcal{L}_1$上升。换句话说，你可以用噪声数据训练，但不能让干净数据的效果变差。

这刚好就是以$\mathcal{L}_0$为主、$\mathcal{L}_1$为辅的主次型多任务学习问题！

无独有偶，去年Google的一篇论文《Gradient-guided Loss Masking for Neural Machine Translation》也给出了类似做法，但细节略有不同。它是通过算每个噪声样本对参数的梯度，只保留与干净数据梯度$\nabla_{\boldsymbol{\theta}} \mathcal{L}_1$夹角小于90度（内积大于0）的样本。也就是说，大家都是以与干净数据梯度的内积为判断依据，不同的是，主次型多任务中，如果内积小于0，则对更新量做一个修正，而在Google的文章中，则是直接删掉对应的样本。

本文小结 #

本文将前一篇文章的平行型多任务学习的结果推广到了“主次型”多任务学习，即多任务学习的目标不再是做好所有的任务，而是以某个任务为主、其余任务为辅，其结果跟原来的平行型多任务学习有不少相似之处，但细微之处又不尽相同，最后介绍了主次型多任务学习的一些经典例子，如正则项、带噪学习等。

转载到请包括本文地址：https://spaces.ac.cn/archives/8907

更详细的转载事宜请参考：《科学空间FAQ》