大气光学质量(Airmass)
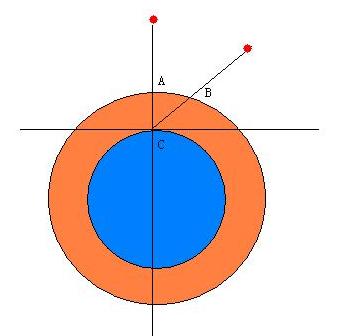
By 苏剑林 | 2010-02-04 | 30985位读者 |天文学中有一个名词Airmass,注意这并非Air mass(空气质量),这是指天顶距等于z的方向上大气光学厚度和天顶方向大气光学厚度之比,我目前也找不到它的中文名称究竟是什么,反正觉得如果译成“大气质量”很怪,就暂且翻译成“大气厚度指数”好了。现在知道它叫做“大气光学质量”了,一般用X表示,如下图中,$X={BC}/{AC}$。
在一片较小的区域内,大气层和地面都可以视为平行平面,这时有一个很好的近似公式:
$$X=\sec z$$
对于现在的中学教材来说,有的读者可能不了解\sec为何物,实际上:$\sec z=\frac{1}{\cos z}$
在60°的时候,airmass约等于2。然而地球是不平坦的,根据不同的精度要求,z的峰值为60-75°。随着天顶角的变大,该公式的准确度迅速降低;该式会在地平线的时候趋于无穷大,而根据实际的弯曲大气情况,airmass通常不会大于40。
实际上,如果不考虑大气折射,把地球看成一个球体,而大气层也视为高度为y的空心球体,只从几何的角度来看,则从天顶角z发出来的光线要穿透的大气厚度为($R_E$为地球半径):
$$s=\sqrt{R_E^2 \cos^2 z+2R_E \cdot y+y^2}-R_E \cdot\cos z$$
或者写成
$$s=\sqrt{(R_E +y)^2 - R_E^2 \sin^2 z}-R_E \cdot\cos z$$
但实际中还必须考虑折射等因素,所以很多插值公式便出来了。例如, Young和Irvine于1967年在$X=\sec z$基础上加入了一个修正因子:
$$X=\sec z_t [1-0.0012(\sec^2 z_t -1)]$$
这里的$z_t$是真实的天顶角,也就是修正了大气折射后的天顶角。这样处理后,天顶角z的峰值可以达到80°。但同样随着天顶角的变大准确度也迅速降低;该式会在z=86.6°时达到11.13的最大值,而在地平线的时候趋于负无穷大。
Hardie在1962年使用了$\sec z-1$的多项式来修正:
$$X=\sec z-0.0018167(\sec z-1)-0.002875(\sec z-1)^2 -0.0008083(\sec z-1)^3$$
这提供了高达85°的峰值,不过和上式一样,该式会达到一个最大值,然后在地平线的时候趋于负无穷大。
1966年Rozenberg提出了
$$X=(\cos z+0.025e^{-11\cos z})^{-1}$$
该法在地平线的时候依旧能够得到合理的值(z=90°时airmass约等于40)
Kasten和Young在1989年发展成
$$X=\frac{1}{\cos z+0.50572(96.07995-z)^{-1.6364}}$$
公式在z接近90°仍然相当合理,在地平线时的结果约为38,注意这里的z必须使用角度为单位。
1994年Young得出
$$X=\frac{1.002432\cos^2 z_t + 0.148386\cos z_t + 0.0096467}{\cos^3 z_ t + 0.149864\cos^2 z_t + 0.0102963\cos z_t + 0.000303978}$$
同样$z_t$为真实天顶角。这条公式可以将误差(即使是地平线的结果)控制在0.0037内。
2002年Pickering派生出了公式
$$X=\frac{x}{\sin(h+\frac{244}{165+47h^{1.1}})}$$
h=90°-z
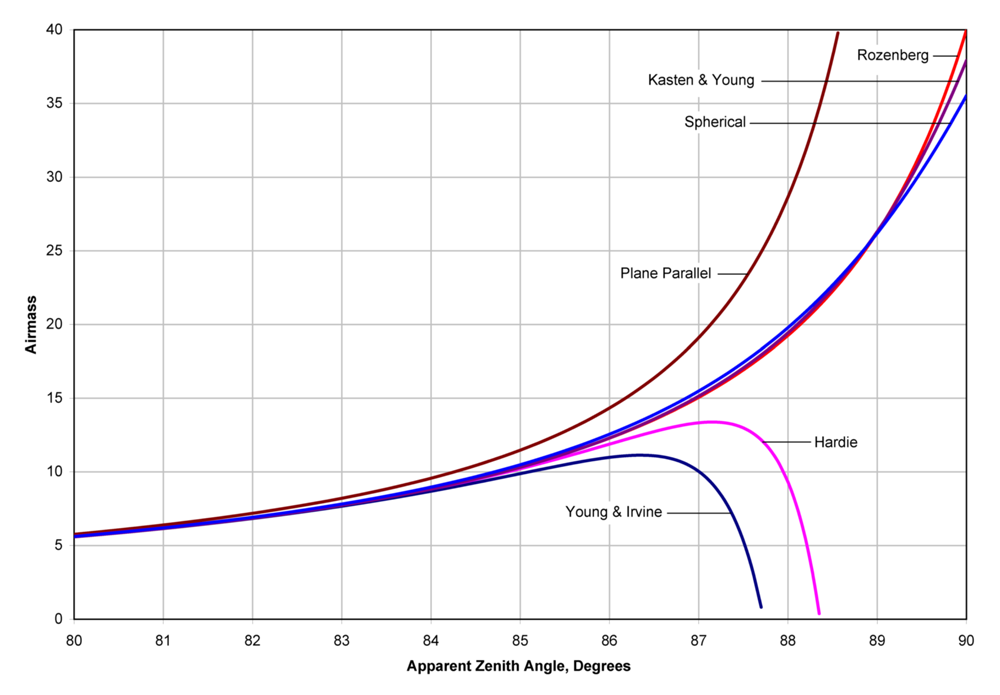
下图的曲线比较了不同的插值公式准确度:
差值公式是从不同的运算过程中导出的近似公式,它只考虑了z这个因素,因为在该问题中,我们只有z这个变量。在一定程度上,插值公式方便了我们的计算。尽管看起来有些公式很麻烦,但对于计算机时代来说,公式的关键是:有效、准确。
更多内容可以参考:http://en.wikipedia.org/wiki/Airmass
转载到请包括本文地址:https://spaces.ac.cn/archives/396
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Feb. 04, 2010). 《大气光学质量(Airmass) 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/396
@online{kexuefm-396,
title={大气光学质量(Airmass)},
author={苏剑林},
year={2010},
month={Feb},
url={\url{https://spaces.ac.cn/archives/396}},
}










最近评论