exp(1/2 t^2+xt)级数展开的图解技术

本文要研究的是关于$t$的函数
$$\exp\left(\frac{1}{2}t^2+xt\right)$$
在$t=0$处的泰勒展开式。显然，它并不困难，手算或者软件都可以做出来，答案是：
$$1+x t+\frac{1}{2} \left(x^2+1\right) t^2+\frac{1}{6}\left(x^3+3 x\right) t^3 +\frac{1}{24} \left(x^4+6 x^2+3\right) t^4 + \dots$$
不过，本文将会给出笔者构造的该级数的一个图解方法。通过这个图解方法比较比较直观而方便地手算出展开式的前面一些项。后面我们再来谈谈这种图解技术的起源以及进一步的应用。

级数的图解方法：说明 #

首先，很明显要写出这个级数，关键是写出展开式的每一项，也就是要求出
$$f_k (x) = \left.\frac{d^k}{dt^k}\exp\left(\frac{1}{2}t^2+xt\right)\right|_{t=0}$$
$f_k (x)$是一个关于$x$的$k$次整系数多项式，$k$是展开式的阶，也是求导的阶数。

这里，我们用一个“点”表示一个$x$，用“两点之间的一条直线”表示“相乘”，那么，$x^2$就可以表示成

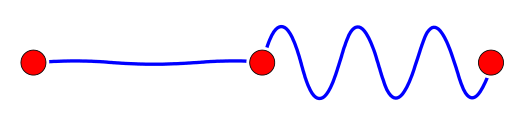
我们用“点”的个数代表着$f_k (x)$的次数，那么$f_k (x)$的每一项都应该有$k$个点，而$f_k (x)$并非总是$k$次的，这时候，我们用“两个点以及它们之间的波浪线”表示“1”，借用物理的术语，可以说这两个点“耦合”成了一个常数。所以，下面的图就表示$f_3(x)$中的$x$：

要注意项的形式跟图的顺序无关，也就是说，下图也表示$f_3(x)$中的$x$：

为了表示项前面的系数，我们在后面添加对应的数字，所以下图表示$f_3(x)$中的$3x$这一项：

我们还需要一个限制，就是“两个波浪线不能出现在相邻的地方”，也就是下面的图是被禁止的：

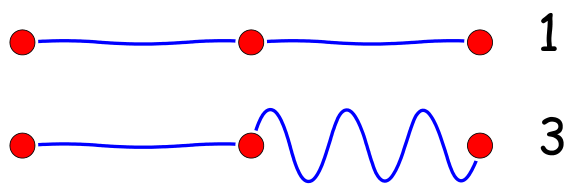
现在，我们不难读出下面的图：

它表示$x^3+3x$，是泰勒展式的三阶项；类似地，图

表示$x^4+6x^2+3$，是泰勒展式的四阶项。

级数的图解方法：递推 #

如果仅仅是上面的图示，那么它仅仅是级数的另外一种写法，并没有给我们带来什么帮助。然而，借助图示可以很直观地帮助我们进行递推，也就是从$k$阶图到$k+1$阶的图的过程。

以从$3$阶到$4$阶的过程为例，3阶的图为

$4$阶的图有4个点，也就是添加1个点。我们想象着，添加的这个点会发出两种“信号”：直线信号和波浪信号。这两种信号会探测原有图的各个点，但两种信号有不同的特点。

直线信号

直线信号是“见好就收”的那种，它对各个点没有分辨力，只要探测到一个点就与之相连，并且停止进一步的探测，因此，经过直线信号的探测，3阶图变为

波浪信号

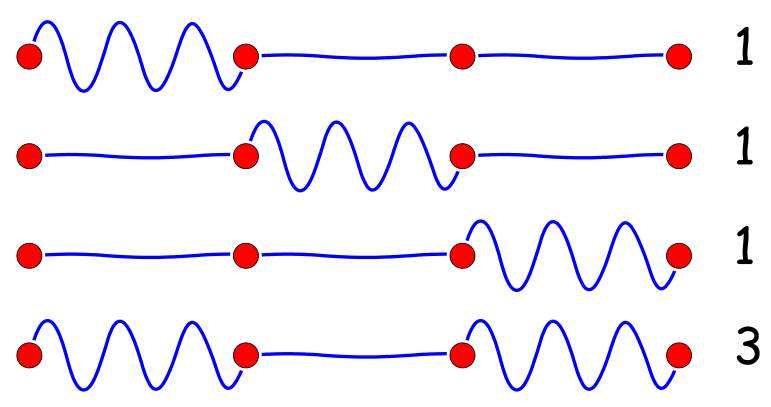
波浪信号与直线信号不同，它对各个点有识别能力，会精细地探测各个可以嵌入的点，然后逐一嵌入到里边去，因此，经过波浪信号的探测，3阶图变为（其中前三个图是等价的）

因此，综合两种信号的探测结果，我们得到四阶图

表示$x^4+6x^2+3$，是泰勒展式的四阶项。

这是一个示例，读者可以结合自己的理解，进一步简化其中的过程。

级数的图解方法：应用 #

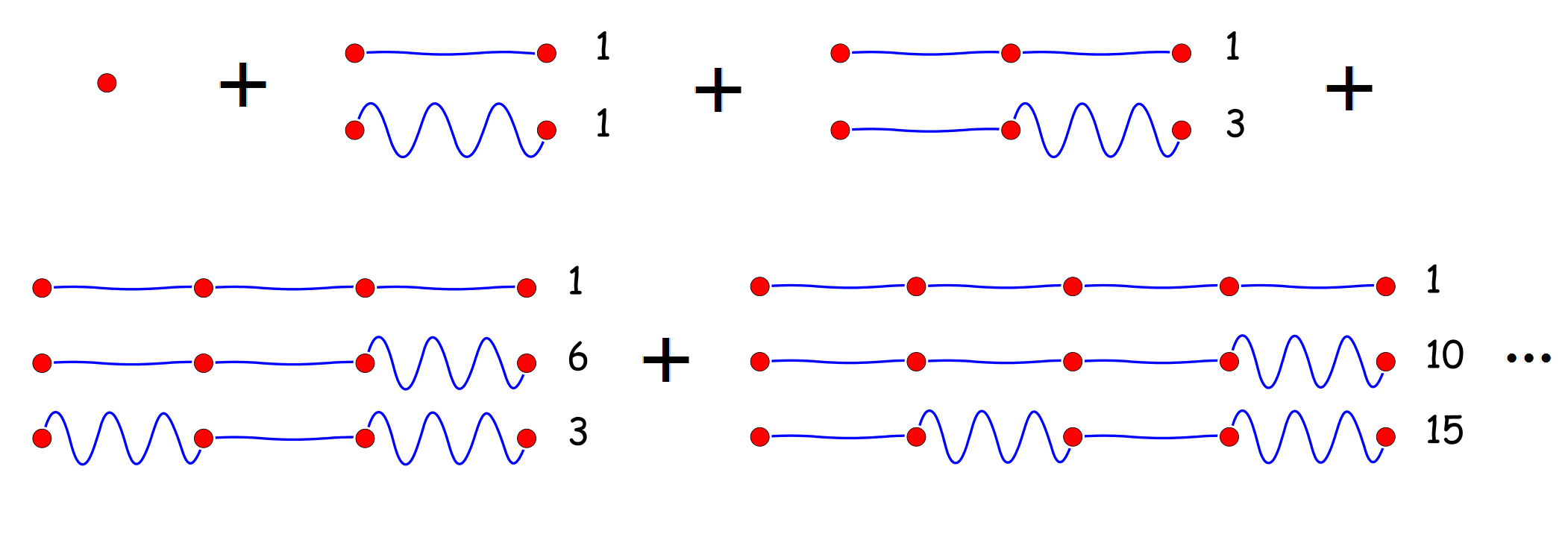
利用上述图解过程，就可以比较快地画出该级数的图

第一项表示$f_1 (x) = x$，它对应着泰勒展式的$xt$项，第二项表示$f_2 (x) = x^2 + 1$，它对应着泰勒展式的$\frac{1}{2!}(x^2 + 1)t^2$项；第三项表示$f_3 (x) = x^3 + 3x$，它对应着泰勒展式的$\frac{1}{3!}(x^3 + 3x)t^3$项，等等。所以
$$\exp\left(\frac{1}{2}t^2+xt\right)=1+x t+\frac{1}{2} \left(x^2+1\right) t^2+\frac{1}{6}\left(x^3+3 x\right) t^3 + \dots$$

显然，如果仅仅是为了展开这个级数，上述工程未免小题大作了。但是，将点和波浪线换成其他意义，就有可能在更复杂的展开式中发挥作用。事实上，我是在研究量子力学微扰技巧的“外源技巧”（泛函导数）中总结出来的这一套方法。在那里，要求
$$\frac{\delta^n}{\delta x^n}\exp\left[\int \left(xf+\frac{1}{2}fL^{-1}f\right)dt\right]$$
泛函导数的求法远比普通导数复杂，因此，如果有这样的一套图示方法来帮助我们进行计算，能够减轻我们的计算量，方便我们对每一项进行推导。而事实上，在泛函导数中，类似的技巧是存在的，这就相当于把各个点换成不同颜色的，将每一项区别开来，可以想象，每一项将会多得多，也复杂得多。当然，这留给以后的文章讲述吧。

转载到请包括本文地址：https://www.spaces.ac.cn/archives/3426

更详细的转载事宜请参考：《科学空间FAQ》