你所没有思考过的平行线问题

本文的主题是平行线，了解数学的朋友可能会想我会写有关非欧几何的内容。但这次不是，本文的内容纯粹是我们从小就开始学习的欧氏几何，基于“欧几里得第五公设”（又称平行公设）。但即便是从小就学习的欧氏几何中的平行线，也许里边的很多问题我们都没有思考清楚。因为平行是几何中非常基本的情形，因此，在讨论这种基本命题的时候，相当容易会出现循环论证、甚至本末倒置的情况。

我们从初中开始就被灌输“同位角相等，两直线平行”、“内错角相等，两直线平行”之类的平行线判断法则，当然，还少不了的是“过直线外一点只能作一条直线与已知直线平行”。但是，这些内容之中，有多少是基本的公理，有多少是可以证明的，该如何证明，我想很多人都理解不清楚，我自己也没有一个很好的答案。那些在初中教授平行线的老师们，估计也没多少个能够把它说清楚的。后来我发现，我居然不会证明“同位角相等，两直线平行”，“欧几里得第五公设”好像并没有告诉我们这个判定法则呀。于是，我翻看了一下初中的数学教科书，发现原来当初“同位角相等，两直线平行”这一判定法则是不加证明地让我们接受的，无怪乎我怎么也想不到关于这一法则的简单的证明...

于是，我想写这篇文章，为大家理解平行线的整个逻辑提供一点参考。

找出平行线 #

一开始我们就声明我们只讨论欧氏几何，因此，我们承认如下公理：

过直线外一点只能作一条直线与已知直线平行。

当然，在欧几里得的《几何原本》中，更基本的是如下四条

1、从一点向另一点可以引一条直线。
2、任意线段能无限延伸成一条直线。
3、给定任意线段，可以以其一个端点作为圆心，该线段作为半径作一个圆。
4、所有直角都相等。

事实上，第一条公理中，还暗含了过两点只能作一条直线，第二条公理中，还暗含了所有直线的长度都是无限的。如果没有这些“暗含”，则以上的公理还不足以构成欧氏几何的基础。另外，不难证明“过两点只能作一条直线”等价于说“平面上两条不同的直线，最多只有一个交点”。

以上内容就是本文的基础了，当然，也是欧氏几何的基础。首先，第五公设说只有一条平行线，那么我们首先把它找出来，找出来的方法如下：

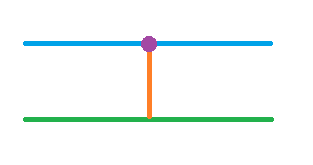
绿色线为已知直线，紫色点为已知点，过紫色点作已知直线的垂线。

注意，我们所做的每一步，都要考虑依据，以避免本末倒置的出现。为什么可以作出已知直线的垂线？首先，我们过紫色点任意作一条直线与绿色线相交，得到两个角∠A和∠B，其中∠A-∠B > 0，当直线以紫色点为中心旋转到右边的时候，必然有∠A-∠B < 0，从而必有某个位置使得∠A=∠B，而∠A+∠B=180°，即∠A=∠B=90°。这本质上是连续函数的介值定理——数学分析里边的内容！你没有看错，就是数学分析，就这么简单的问题也需要用到。如果真的要将几何严格化，必须要借助代数这一工具！

接下来，我们过紫色点，作一条直线（下面的蓝色线），垂直于上一步作出来的橙色线。

下面我们可以证明，蓝色线平行于绿色线。证明的思想很简单，整个图形是关于橙色线对称的，如果蓝色线和绿色线在某一边相交，那么必然也在另外一边相交，从而有两个交点——这与已知的公理“平面上两条不同的直线，最多只有一个交点”矛盾。因此，两者只能是平行。

现在我们就找出了一条平行线了，而根据第五公设，只有一条这样的线，所以这条线就是唯一一条了。

“内错角相等，两直线平行” #

下面我们来证明“内错角相等，两直线平行”。个人认为，这个一点都不简单...

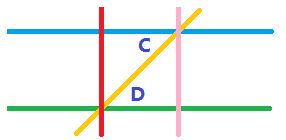
首先我们有两条平行线：蓝色线和绿色线，黄色线是跟平行线相交的直线，从而得到两个内错角C和D。紧接着，过C角处的交点，作粉红色的线垂直于蓝色线，然后可以证明粉红色线也垂直于绿色线。这步很显然，但也需要证明。如果粉红色线不垂直于绿色线，那么可以按前面的方法，坐出另外一条过同样的点而又与蓝色线平行的线来，从而过同一点有两条不同的直线与蓝色线平行，矛盾。顺便地，我们容易证明红色线平行于粉红色线。

现在我们得到了一个矩形——四个内角都是90°的图形。于是可以利用矩形的对称性来证明两个三角形全等，即三条边对应相等的两个三角形全等，从而内错角相等。而这个判定法则，源于三角形的稳定性——也是几何公理。

可是别忘了，我们还没有证明矩形的对边相等！！这里的矩形定义为四个内角都是90°的四边形，因此并没有包含对边相等这个条件，需要我们证明。当然，不困难，利用对称性，将矩形对折过来，根据我们平行线的作法（两次垂直），中点处的平行线，就是对称轴，因此对折过来后就重合了。（这里说的比较通俗，可以用数学的语言写出来~请读者自己试试，对称性是关键。）

一点点总结 #

为了说明平行这件事情，我们花了那么多篇幅，而且还不知道说清楚了没有。因此，涉及到这些基本问题，需要步步质问，步步为营，才不至于陷入逻辑上的矛盾。当然，有没有必要做这件事情，就见仁见智了。

有些地方可能我也没有论证清楚，也有可能出现逻辑矛盾，希望读者发现后不吝批评。

转载到请包括本文地址：https://spaces.ac.cn/archives/3243

更详细的转载事宜请参考：《科学空间FAQ》