矩阵描述三维空间旋转

本节简单介绍用矩阵来描述旋转。在二维平面上，复数无疑是描述旋转的最佳工具；然而推广到三维空间中，却要动用到“四元数”了。为了证明四元数的相关结论，我们需要三维旋转的矩阵描述。最一般的旋转运动为：绕某一根轴旋转$\theta$角度。这样我们就需要三个参数来描述它：确定一根轴至少需要两个参数，确定角度需要一个参数。因此，如果要用“数”来描述三维空间的伸缩和旋转的话，“三元数”显然是不够的，完成这一目的至少需要四元数。这也从另外一个角度反映了三元数的不存在性。

矩阵方法
首先我们认识到，如果旋转轴是坐标轴之一，那么旋转矩阵将是最简单的，比如向量$\boldsymbol{x}=(x_0,y_0,z_0)^{T}$绕$z$轴逆时针旋转$\theta$角后的坐标就可以描述为
$$\begin{equation}
\boldsymbol{R}_{\theta}\boldsymbol{x}\end{equation}$$
其中
$$\begin{equation}\label{xuanzhuanjuzhen}
\boldsymbol{R}_{\theta}=\left[ \begin{array}{\cdot {20}{c}}
\cos\theta&{ - \sin\theta}&0\\
\sin\theta & \cos\theta &0\\
0&0&1
\end{array} \right]
\end{equation}$$
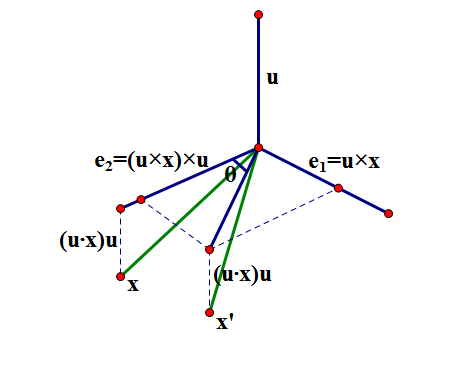
如果旋转轴不是坐标轴，而是由单位列向量$\boldsymbol{u}=(x_1,y_1,z_1)$确定，那么同时就确定了与$\boldsymbol{u}$垂直的一个平面，在此平面上找到两个正交的单位列向量$\boldsymbol{e}_1,\boldsymbol{e}_2$，用$\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{u}$就可以建立一个新直角坐标系（右手架），设在此坐标系之下原来的$\boldsymbol{x}$向量的坐标为$\boldsymbol{\xi}=(\xi_1,\xi_2,\xi_3)^T$，则
$$\begin{equation}
\left[ \boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{u} \right] \boldsymbol{\xi}=\boldsymbol{x}
\end{equation}$$
在新坐标系下描述旋转是方便的，它就是矩阵$\eqref{xuanzhuanjuzhen}$。绕$\boldsymbol{u}$轴逆时针旋转$\theta$角后，坐标为
$$\begin{equation}
\boldsymbol{R}_{\theta} \boldsymbol{\xi}=\boldsymbol{R}_{\theta}\left[ \boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{u} \right]^{-1}\boldsymbol{x}
\end{equation}$$
上面是在$\boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{u}$坐标系的坐标，变为我们最初的直角坐标系，那就是
$$\begin{equation}\label{xuanzhuan}
\left[ \boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{u} \right]\boldsymbol{R}_{\theta}\left[ \boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{u} \right]^{-1}\boldsymbol{x}
\end{equation}$$
$\eqref{xuanzhuan}$式就是旋转之后的坐标。它描述了三维空间中最一般的旋转。注意矩阵$\left[ \boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{u} \right]$ 是一个正交矩阵，因此它的逆就是$\left[ \boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{u} \right]^{-1}=\left[ \begin{array}{*{20}{c}}\boldsymbol{e}_1^T \\ \boldsymbol{e}_2^T \\ \boldsymbol{u}^{T}\end{array} \right]$，因此旋转后坐标为
$$\begin{equation}\label{xuanzhuanzuobiao3}
\left[ \boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{u} \right]\boldsymbol{R}_{\theta}\left[ \begin{array}{\cdot {20}{c}}\boldsymbol{e}_1^T \\ \boldsymbol{e}_2^T \\ \boldsymbol{u}\end{array}\right]\boldsymbol{x} =\left[ \boldsymbol{e}_1,\boldsymbol{e}_2,\boldsymbol{u} \right]\boldsymbol{R}_{\theta}\left[ \begin{array}{\cdot {20}{c}}\boldsymbol{e}_1 \cdot \boldsymbol{x} \\ \boldsymbol{e}_2 \cdot \boldsymbol{x}\\ \boldsymbol{u} \cdot \boldsymbol{x}\end{array} \right]
\end{equation}$$

剩下就是$\boldsymbol{e}_1,\boldsymbol{e_2}$的确定问题。如果无法很快找出满足条件的两个向量来，那么可以利用向量的叉积：
$$\begin{equation}\label{chaji}
\boldsymbol{e}_1=\frac{\boldsymbol{u}\times\boldsymbol{x}}{|\boldsymbol{u}\times\boldsymbol{x}|},\boldsymbol{e}_2=\frac{\boldsymbol{u}\times(\boldsymbol{u}\times\boldsymbol{x})}{|\boldsymbol{u}\times(\boldsymbol{u}\times\boldsymbol{x})|}=\frac{(\boldsymbol{u}\cdot\boldsymbol{x})\boldsymbol{u}- \boldsymbol{x}}{|\boldsymbol{u}\times\boldsymbol{x}|}
\end{equation}$$

叉积的好处是明显的，将$\eqref{chaji}$代入$\eqref{xuanzhuanzuobiao3}$，得到
$$\begin{equation}\label{juzhenxuanzhuanhuajian}
\begin{aligned}
&\left[ \frac{\boldsymbol{u}\times\boldsymbol{x}}{|\boldsymbol{u}\times\boldsymbol{x}|},\frac{(\boldsymbol{u}\cdot\boldsymbol{x})\boldsymbol{u}- \boldsymbol{x}}{|\boldsymbol{u}\times\boldsymbol{x}|},\boldsymbol{u} \right]\boldsymbol{R}_{\theta}\left[ \begin{array}{\cdot {20}{c}}0 \\ \frac{(\boldsymbol{u} \cdot \boldsymbol{x})^2-\boldsymbol{x}^2}{|\boldsymbol{u}\times\boldsymbol{x}|}\\ \boldsymbol{u} \cdot \boldsymbol{x}\end{array} \right]\\
=&\left[ \frac{\boldsymbol{u}\times\boldsymbol{x}}{|\boldsymbol{u}\times\boldsymbol{x}|},\frac{(\boldsymbol{u}\cdot\boldsymbol{x})\boldsymbol{u}- \boldsymbol{x}}{|\boldsymbol{u}\times\boldsymbol{x}|},\boldsymbol{u} \right]\left[ \begin{array}{\cdot {20}{c}} |\boldsymbol{u}\times \boldsymbol{x}| \sin\theta \\ -|\boldsymbol{u}\times \boldsymbol{x}|\cos\theta \\ \boldsymbol{u} \cdot \boldsymbol{x}\end{array} \right]\\
=&\left(\boldsymbol{u}\times\boldsymbol{x} \right)\sin\theta-\left[(\boldsymbol{u}\cdot\boldsymbol{x})\boldsymbol{u}- \boldsymbol{x}\right]\cos\theta+(\boldsymbol{u}\cdot\boldsymbol{x})\boldsymbol{u}\\
=&\left(\boldsymbol{u}\times\boldsymbol{x} \right)\sin\theta+\left[(\boldsymbol{u}\times\boldsymbol{x})\times\boldsymbol{u}\right]\cos\theta+(\boldsymbol{u}\cdot\boldsymbol{x})\boldsymbol{u}
\end{aligned}
\end{equation}$$
这被称为Rodrigues旋转公式，它是用向量描述三维空间旋转最简单的形式。写成最后的形式是因为它有明显的几何意义，事实上可以完全不用矩阵的分析，只是利用几何方法和向量叉积就可以推导出$\eqref{juzhenxuanzhuanhuajian}$的最后一式来。另外如果$\boldsymbol{x} \perp \boldsymbol{u}$（事实上在实际应用中，这一条件并不算苛刻。），那么坐标旋转公式将会相当简单：
$$\begin{equation}
(\boldsymbol{u}\times\boldsymbol{x})\sin\theta +\boldsymbol{x}\cos\theta
\end{equation}$$

几何方法

旋转示意图

已知单位向量$\boldsymbol{u}$是旋转轴，求向量$\boldsymbol{x}$绕轴$\boldsymbol{u}$逆时针旋转$\theta$角之后的坐标。我们用$\boldsymbol{u}$跟$\boldsymbol{x}$作叉积$\boldsymbol{e}_1=\boldsymbol{u}\times\boldsymbol{x}$，得到一个与$\boldsymbol{u}$和$\boldsymbol{x}$都垂直的向量；再做叉积$\boldsymbol{e}_2=(\boldsymbol{u}\times\boldsymbol{x})\times\boldsymbol{u}$，得到一个与$\boldsymbol{u}$和$\boldsymbol{x}$和$\boldsymbol{u}$共面的向量，且这个向量与$\boldsymbol{u}\times\boldsymbol{x}$等长，与$\boldsymbol{u}$和$\boldsymbol{u}\times\boldsymbol{x}$都垂直。

注意到
$$(\boldsymbol{u}\times\boldsymbol{x})\times\boldsymbol{u}=\boldsymbol{x}-(\boldsymbol{u}\cdot\boldsymbol{x})\boldsymbol{u}$$
也就是说向量$\boldsymbol{x}$在平面$\boldsymbol{e}_1 ,\boldsymbol{e}_2$上的投影就是$\boldsymbol{e}_2$，而在$\boldsymbol{u}$轴上的投影是$(\boldsymbol{u}\cdot\boldsymbol{x})\boldsymbol{u}$，要注意旋转的时候只有在$\boldsymbol{e}_1 ,\boldsymbol{e}_2$平面、也就是旋转平面上的分量有变化，描述旋转平面上的变换是简单的，它只不过是
$$\boldsymbol{e}_2 \cos\theta +\boldsymbol{e}_1\sin\theta$$

再加上$\boldsymbol{u}$轴的分量$(\boldsymbol{u}\cdot\boldsymbol{x})\boldsymbol{u}$就得到了旋转后的坐标，也就是
$$\left(\boldsymbol{u}\times\boldsymbol{x} \right)\sin\theta+\left[(\boldsymbol{u}\times\boldsymbol{x})\times\boldsymbol{u}\right]\cos\theta+(\boldsymbol{u}\cdot\boldsymbol{x})\boldsymbol{u}$$
这样我们就重新得到了$\eqref{juzhenxuanzhuanhuajian}$。

转载到请包括本文地址：https://spaces.ac.cn/archives/2224

更详细的转载事宜请参考：《科学空间FAQ》

打赏

微信打赏

支付宝打赏

因为网站后台对打赏并无记录，因此欢迎在打赏时候备注留言。
你还可以点击这里或在下方评论区留言来告知你的建议或需求。