也许大家会觉得，相对论中有一个因子
$$\gamma =\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}$$
因此，相对论的效应只有在高速情况下，即v比较接近于c的情况下才会凸显出来。这在一般情况下是正确的，但是却不全对。因为存在相当明显的、速度低于1mm/s的相对论效应——那就是几乎人尽皆知的“磁”。

之前已经提及过，磁场可以解释为电场的相对论效应，因此所有电磁现象都可以归因为电场和相对论。事实上，这是正确的，只是教科书上并没有明确说出这一点而已。于是我们就不难理解“为什么电磁学的麦克斯韦方程组会与相对论协调”、“为什么电场与磁场的表现如此相似”等等问题了，因为它们的探究本身就在相对论的框架下，磁场和电场都是一个东西的结果。

下面的内容基本上都出自《看得见的相对论》，这是一本科普类的小书，但它着眼于用直观的方式给我们相对论的理解，可以说是相对论（包括广义相对论）的文字版本，而不是公式版本（当然里边也有一些相当易懂的公式）。

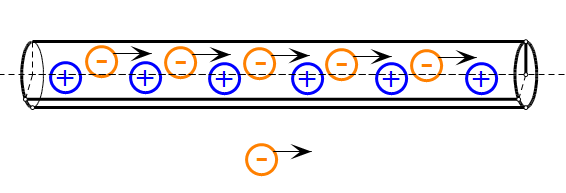
让我们考虑一根有恒定电流的直导线，并假设导线内没有电阻（这是相当理想的情况，但是有电阻也不会明显改变结果）。我们知道，电流的产生实际上是带有负电荷的电子在定向移动，导线内的正离子并没有移动。设电子移动的速度为v，电子的速度不大于1mm/s，如下图：

电的相对论效应

电的相对论效应

想象导线的外边有一个电子，假如它静止，那么它将不会受到任何力的作用，但是如果它跟导线内的电子做相同的运动（同速度、同向），那么电磁学知识告诉我们，电子会趋向导线，受到正比于$v^2$的力的作用。这一项力就是我们所说的电生磁效应了。下面我们用相对论来解释这一效应 。

再次想象，我们“坐在”一个电子上边，那么在我们看来，所有的电子都是静止的，而正离子和导线本身倒是以速度v反向运动了。由于相对论效应，运动的长度会发生收缩，于是导线的体积也相应变为原来的
$$\sqrt{1-\frac{v^2}{c^2}}$$

所以导线内的正电荷密度变为原来的
$$\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}\approx 1+\frac{v^2}{2c^2}$$

但是电子密度没有变化，因此导线内相当于净剩下正电荷了，其数目正比于
$$\frac{1}{\sqrt{1-\frac{v^2}{c^2}}}-1 \approx \frac{v^2}{2c^2}$$

导线内有正比于$\frac{v^2}{2c^2}$的正电荷，而外边是一个负的电子，所以两者自然相吸，而且根据库仑定律，两者的力是正比于电荷量之积的，因此自然也正比于$\frac{v^2}{2c^2}$了，即正比于$v^2$。这就解释了电生磁现象。也就是说，在如此低的速度之下也会有明显的相对论效应。

总结

上面可以总结为：没有相对论，就没有磁效应。因此，相对论的长度收缩、时间延缓等等各种效应都是实实在在的，而不是观测者的“幻象”。一般而言，相对论效应都是不明显的，但是对于电磁学来说，库仑力是如此地大，以至于微弱的相对论效应被放大得如此明显。另一方面，这个观点也让人耳目一新，难道，我们认识了好几千年的磁效应，仅仅是一个“子虚乌有”的东西？

转载到请包括本文地址：https://spaces.ac.cn/archives/1987

更详细的转载事宜请参考：《科学空间FAQ》

如果您还有什么疑惑或建议，欢迎在下方评论区继续讨论。

如果您觉得本文还不错，欢迎分享/打赏本文。打赏并非要从中获得收益，而是希望知道科学空间获得了多少读者的真心关注。当然，如果你无视它，也不会影响你的阅读。再次表示欢迎和感谢！

如果您需要引用本文，请参考：

苏剑林. (May. 11, 2013). 《电的相对论效应——磁“子虚乌有”？ 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/1987

@online{kexuefm-1987,
        title={电的相对论效应——磁“子虚乌有”？},
        author={苏剑林},
        year={2013},
        month={May},
        url={\url{https://spaces.ac.cn/archives/1987}},
}