黑洞融合的简单模拟
By 苏剑林 | 2012-12-18 | 22570位读者 |在天文爱好者眼中,黑洞是一个球体,其半径为$\frac{2GM}{c^2}$;这是广义相对论的施瓦兹黑洞的结果,也从经典力学推导推导出来,虽然用经典力学是错误的,但是对于多数的天文爱好者(包括笔者)来说,这是目前唯一的一种可行的理解方法(广义相对论那些复杂推导会让我们很崩溃的)。当然,事实上,黑洞不是一个球体,它只是一个密度很大的点。至于密度有多大,目前公认的说法是无穷大,但是严格的物理是不接受这个说法的,或者说,物理是不会接受任何无穷大的说法,所以现在积极发展量子引力理论来统一相对论和量子力学,不过这是另话了。$\frac{2GM}{c^2}$只不过是黑洞的视界,视界之内,我们就什么也不知道了。本文主要就从经典力学的角度探讨一下两个黑洞的合并过程中其视界的变化。读者将会发现,这些视界的形状相当有趣。
经典力学中的黑洞是这样定义的:天体表面的逃逸速度超过了光速,于是连光都无法逃脱,所以这个“洞”就很黑。也就是说,光子的总能量(引力势能与动能之和,经典力学意义下的)要为负,负数表示受到束缚。用数学公式来讲,就是:
$$\frac{1}{2}mc^2 - \frac{GM_1 m}{r_1}-\frac{GM_2 m}{r_2}-...-\frac{GM_n m}{r_n} \leq 0$$
其中$-\frac{GMm}{r}$表示光子的引力势能。也就是说,假如有n个质点,那么它们造成的黑洞视界由以下方程确定:
$$ \frac{M_1}{r_1}+\frac{M_2}{r_2}+...\frac{M_n}{r_n} \geq \frac{c^2}{2G} $$
建立坐标系就可以描述出这些曲面的形状来。我们不妨先来看一下两个等质量黑洞的情况,在观看下面的模拟结果之前,读者不妨先闭上自己的眼睛,想象这些曲面大概会是什么形状的?这是一种相当重要的训练,它为你建立一系列的物理直觉,有助于我们检验最后结果的正确性。
两个等质量黑洞合并的过程中,视界的方程是这样的:
$$ \frac{1}{r_1}+\frac{1}{r_2} \geq \frac{c^2}{2GM} $$
建立适当的直角坐标系,其方程就可以表示出来:
$$ \frac{1}{\sqrt{x^2+y^2+z^2+d^2+2dx}}+\frac{1}{\sqrt{x^2+y^2+z^2+d^2-2dx}} \geq \frac{c^2}{2GM} $$
其中2d表示两个天体的距离,黑洞合并的过程中也就是d不断减少直到为0的情况。下面是一系列的模拟图:
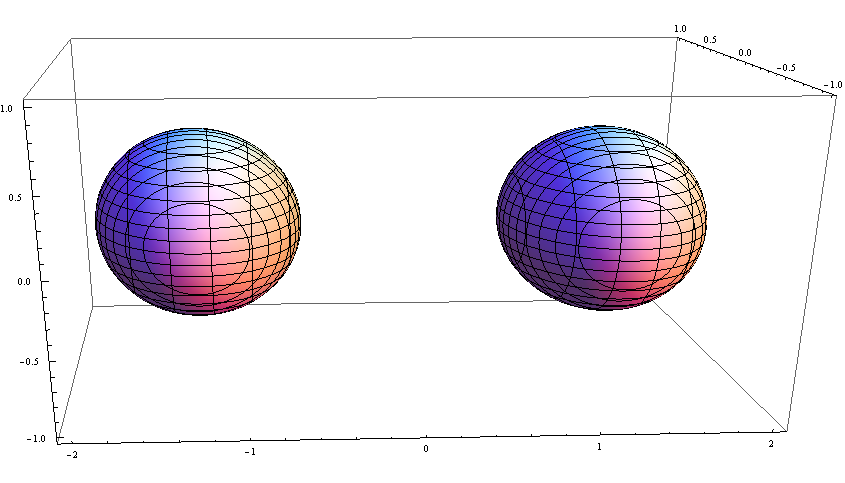
距离很远时,视界就是两个球体:
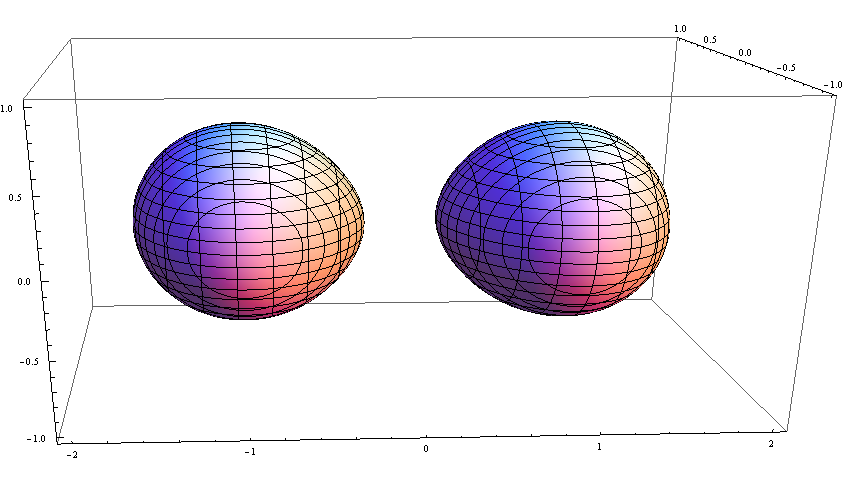
逐渐靠近时,由于相互之间的引力叠加,视界区域变大:
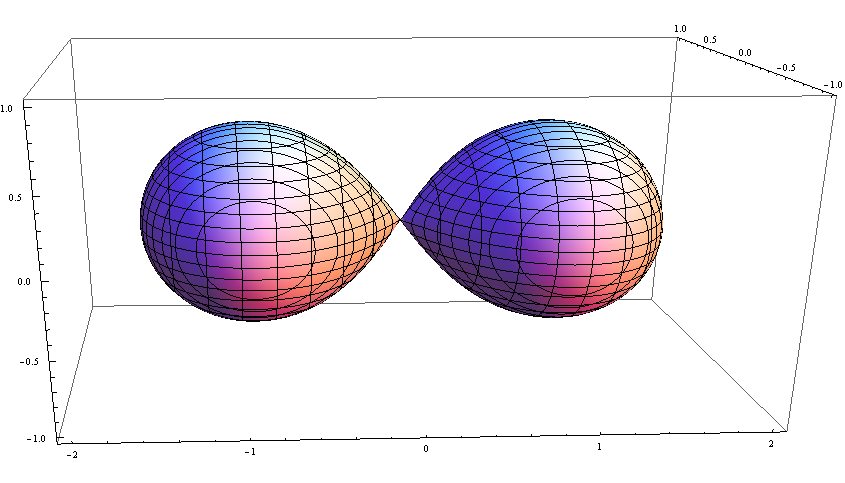
视界开始交汇:
视界慢慢融合:
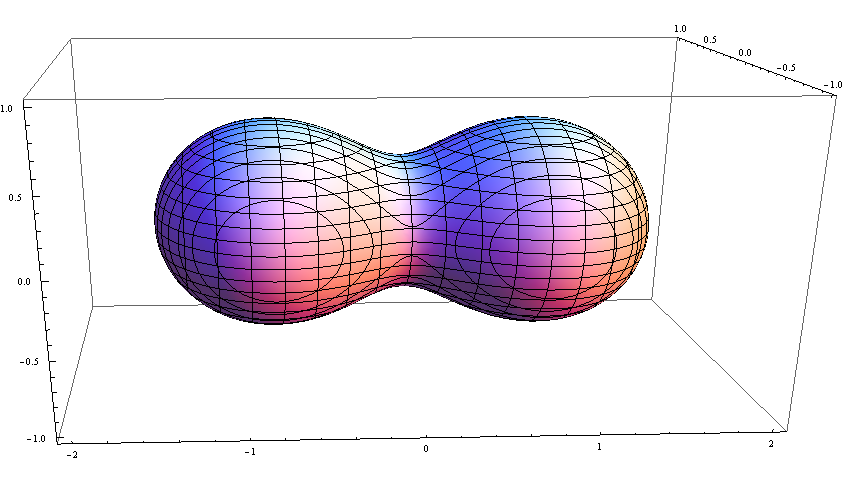
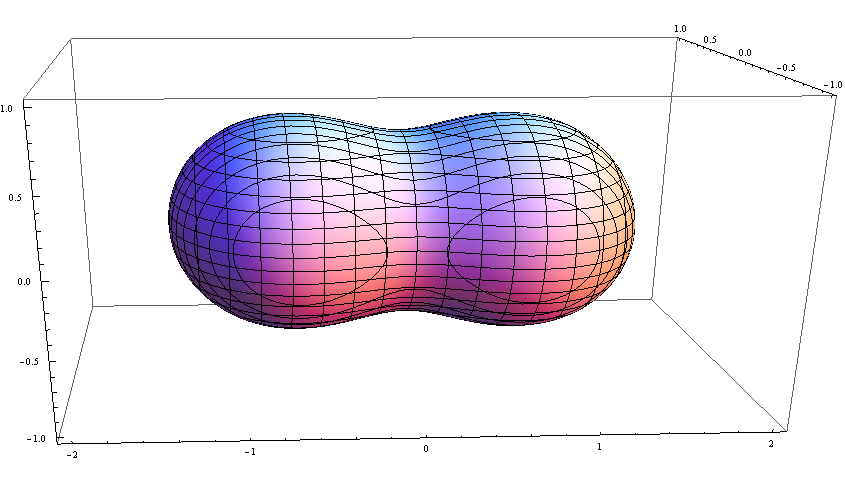
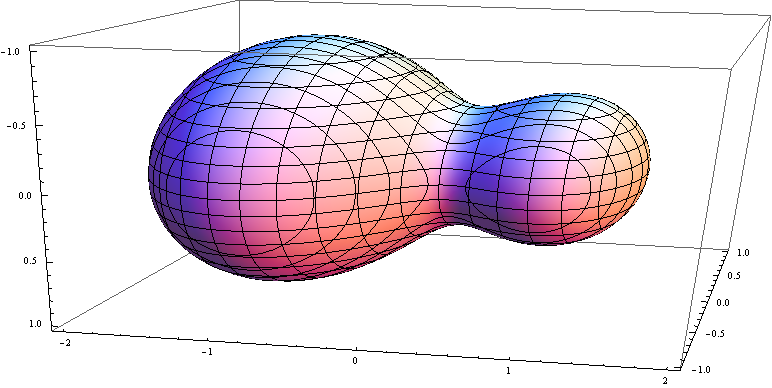
挺像花生的:
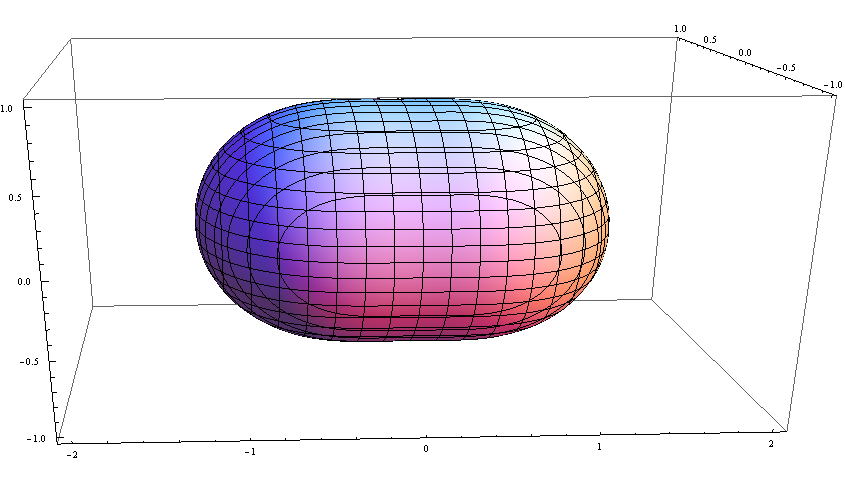
很接近一个球体了:
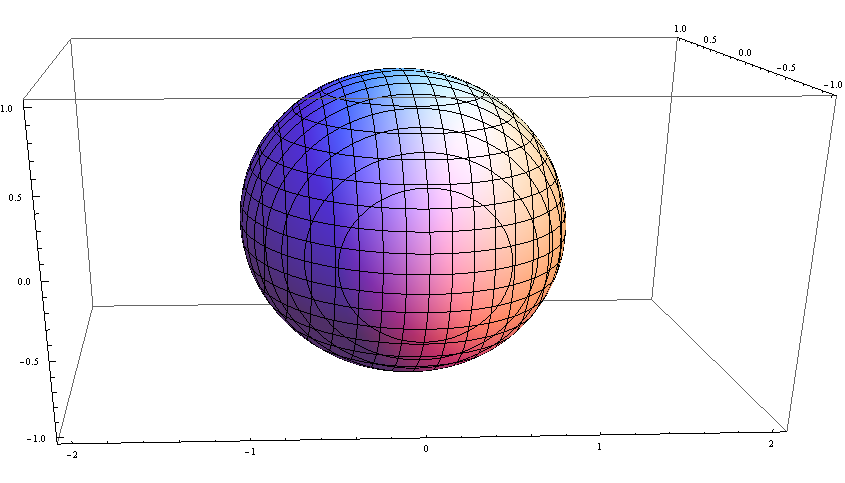
最终结果,变成一个球体:
其表面积比两个的总和要大。
这是我做的一个小动画(很简陋的逐帧叠加):
其实这个形状跟天体物理中的洛希瓣本质是一样的。这个过程我发现其实有点像细胞分裂的逆过程呢!
如果质量不相等,那么怎么样呢?请看:
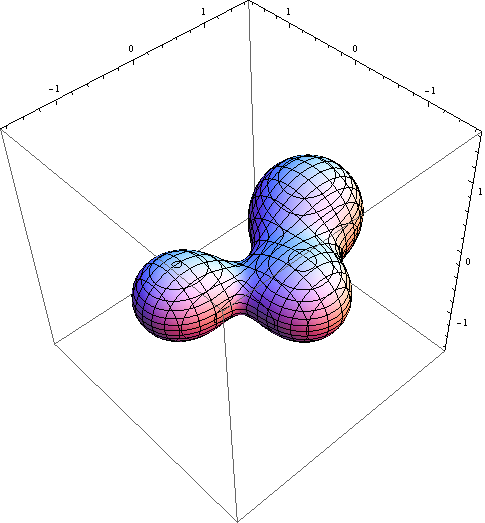
多个黑洞合并就更有趣了:
笔者最近在学习理论物理的内容,虽然很有趣,但是数学是很繁杂的。为了不至于在复杂的数学海洋中迷失了物理的本性,所以我不时要寻找一些有趣的玩儿来活跃一下大脑思维。本文也是这样的情境下的产物。虽然经典力学的分析并不正确,但是还是能够让我们瞧个端倪,这已经足够了。不管怎样,这只是为了有一个物理直观感觉和几何欣赏而已。当然,还锻炼了我的数学软件使用技术,这些图都是用Mathematica 8生成的。
转载到请包括本文地址:https://spaces.ac.cn/archives/1825
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Dec. 18, 2012). 《黑洞融合的简单模拟 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/1825
@online{kexuefm-1825,
title={黑洞融合的简单模拟},
author={苏剑林},
year={2012},
month={Dec},
url={\url{https://spaces.ac.cn/archives/1825}},
}







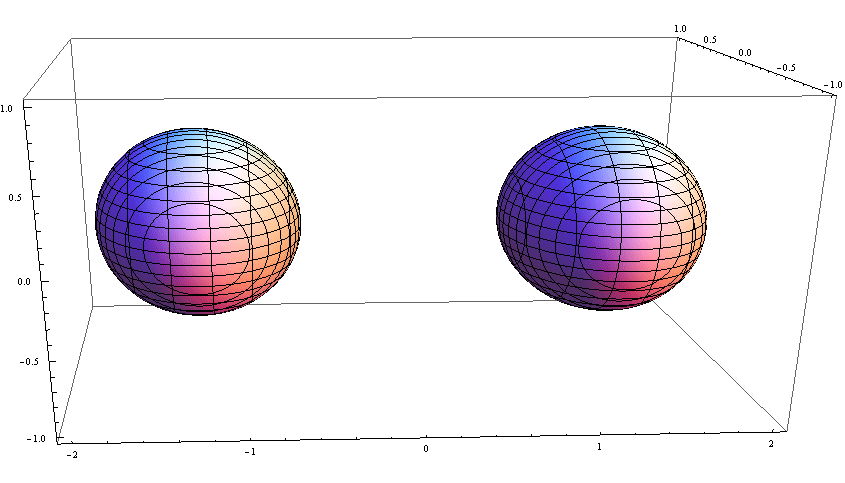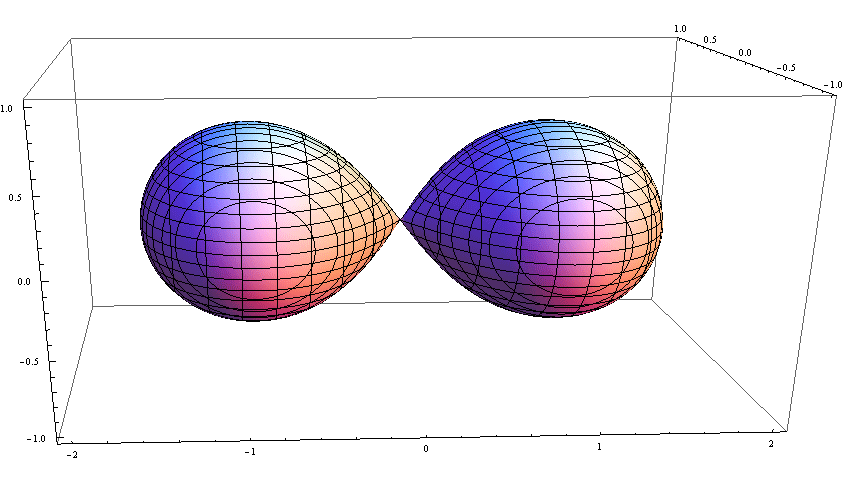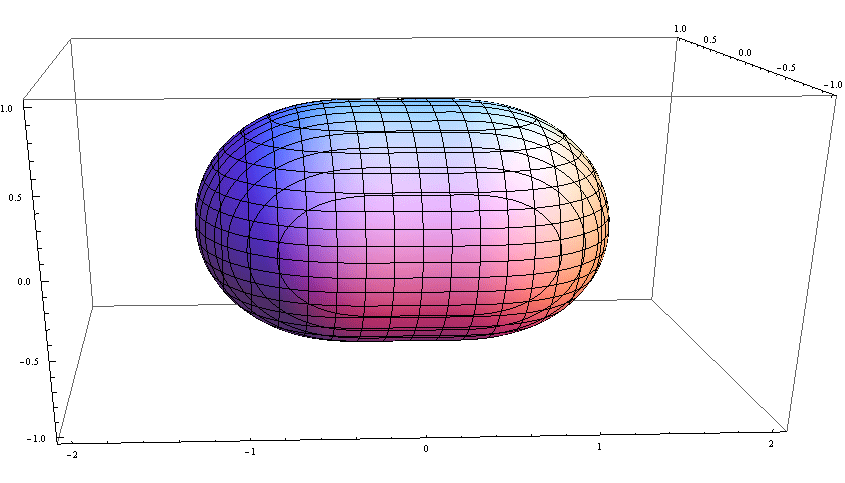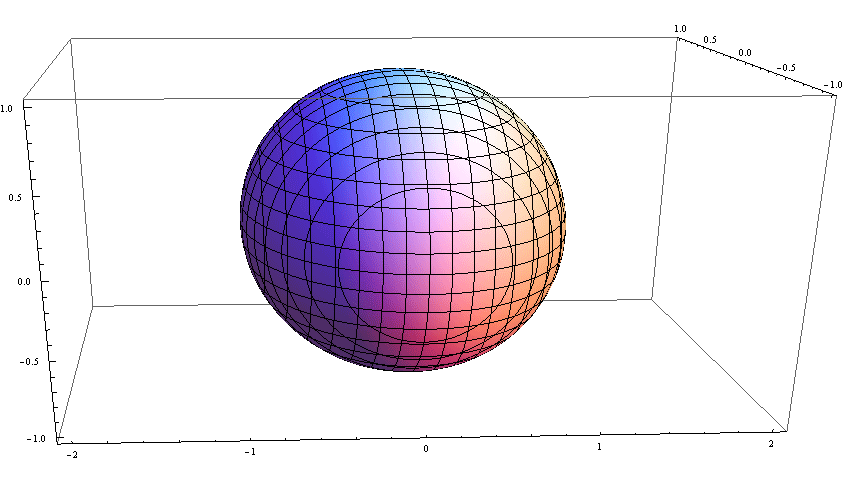



December 18th, 2012
很像细胞融合……离心、振动、电刺激……
March 2nd, 2022
我有点想不通,从直觉上,两黑洞中间的区域引力方向相反,互相抵消,视界面应该是向里挤压才对,怎么会突出来一个尖呢?从牛顿引力来推导,我感觉黑洞合并的过程,视界面是越来越接近奇点,也就是互相接近的一侧变得越来越薄,合并的一刻两个奇点直接撞上了。