哥德巴赫猜想浅谈1
By 苏剑林 | 2012-10-06 | 17601位读者 |高斯说过“数学是科学的皇后,而算术则是数学的女王。”这里的“算术”,其实就是我们现在所说的数论。从很小的时候开始,我便对数论情有独钟。虽然后来接触了很多更为有趣的数学分支,但是对数学的热情依然不减。我想,这大概是因为小时候的情结吧。小学时候,小小年纪的我,刚刚学完素数、合数、约数、整除等等概念,对数字尤其有兴趣。我想,在那时候我唯一能够读懂的数学难题只有数论这一领域吧。比如费马大定理,$x^n+y^n=z^n$,对于n大于2没有正整数解,很容易就知道它在讲什么;再比如,哥德巴赫猜想,每个大于4的偶数都可以分拆成两个奇素数之和,也很简单就弄懂它讲的是什么。所以,小小的我看懂了这些问题后就饶有兴致地摆弄数字啦,也许正因为如此,才让我对数字乃至对数学都有深厚的爱。
哥德巴赫猜想,无疑是数论中的一个璀璨明珠,可是目前来讲,它还是可望不可即的。一个看似如此简单的猜想,却困惑了数学家几百年,至今无人能解。尽管如此,我还是愿意细细地研究它,慢慢地品味它,在“论证”、或者说验算它的时候,欣赏到数学那神秘的美妙。本文主要就是研究给定偶数的“哥德巴赫分拆数”,即通过实际验算得出每个偶数分拆为两个素数之和的不同分拆方式的数目,比如6=3+3,只有一种分拆方式;8=3+5=5+3;有两种分拆方式;10=3+7=5+5=7+3,有三种分拆方式;等等。偶数2n的分拆数记为$G_2 (2n)$。
(这里定义的“分拆数”跟网上以及一般文献中的定义不同,这里把3+5和5+3看成是两种分拆方式,而网上一般的定义是只看成一种。我这里的定义的好处在于分拆方式的数目实际表示了分拆中涉及到的所有素数的个数。)
哥德巴赫猜想很难,这话没错,但是事实上哥德巴赫猜想是一个非常弱的命题。它说“每个大于4的偶数至少可以分拆成两个奇素数之和”,用上面的术语来说,就是每个偶数的“哥德巴赫分拆数”大于或等于1。可是经过实际验算发现,偶数越大,它的哥德巴赫分拆数越大,两者整体上是呈正相关关系的,比如$G_2 (100)=12,G_2 (1000)=56,G_2 (10000)=254$......所以,从强弱程度上来讲,这和“少于n的素数至少有一个”是差不多的(当然,难度有天壤之别)。
为什么这么弱的一个命题,难度有如此之大呢?其实证明哥德巴赫猜想有一个很基本的思路,就是筛法,有点类似于埃拉托斯特尼筛法。我们可以很合理地估计每个偶数的哥德巴赫分拆数,可是我们从无法从细节上严格地证明它,这就是困难之处。正如哈代(Hardy)所说“我们不是在原则上没有成功,而是在细节上没有成功。”
下表是我用Python得出的哥德巴赫分拆数表
(限于篇幅,只列出了100以内的偶数,附件有10000以内的分拆数表)
偶数 分拆数
6 1
8 2
10 3
12 2
14 3
16 4
18 4
20 4
22 5
24 6
26 5
28 4
30 6
32 4
34 7
36 8
38 3
40 6
42 8
44 6
46 7
48 10
50 8
52 6
54 10
56 6
58 7
60 12
62 5
64 10
66 12
68 4
70 10
72 12
74 9
76 10
78 14
80 8
82 9
84 16
86 9
88 8
90 18
92 8
94 9
96 14
98 6
100 12
整体上来讲,n越大,$G_2 (2n)$就越大,但这又不是全局规律。比如96的分拆数是14,可是98却降到了6,100又升到了12,起伏不定,难以捉摸,似乎没有丝毫规律可寻。
其实,分拆数和偶数2n所包含的素因子有关。素因子越少,那么基本上分拆数相对也大一些。那么有没有一个“指标”,或者说近似公式,来给出$G_2 (2n)$的上限或下限呢?BoJone经过验算研究,得出一个经验公式:
$$G_2 (2n) > \frac{2n}{ln^2 (2n)} (n>3)$$
我们或许还记得公式$\frac{2n}{ln (2n)}$其实就是素数定理给出的公式,如果说因子$\frac{1}{ln (2n)}$是一次筛法(筛选出小于2n的素数)得出的结果,那么$\frac{1}{ln^2 (2n)}$实际上相当于进行了两次筛法。所以哥德巴赫猜想可以粗糙地理解为自然数经过两次筛法的过滤之后,还有一些“精华”留下来。
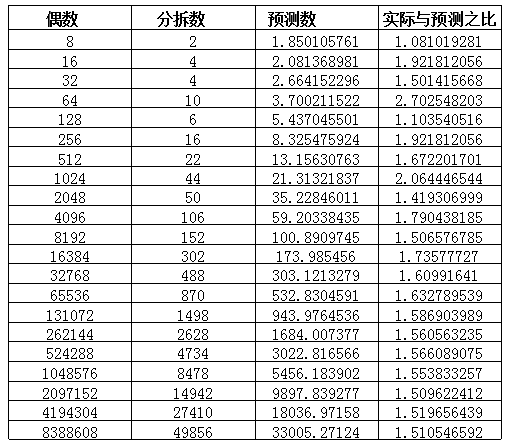
如果没有办法寻找到分拆数的一般规律,那么能不能先研究对于某一类偶数的分拆数规律呢?既然分拆数跟素因子有关,所以我很自然地联想到了$2^n$这一类数。下面是这一类数的分拆表
其中预测数是$\frac{2^n}{ln^2(2^n)}$。当n比较大的时候,$\frac{2^n}{ln^2(2^n)}$的预测效果稳定下来了,基本保持在分拆数的$\frac{2}{3}$左右,当然后边的我还没有验算,因为当n增大时,超出了我编写的程序的计算范围了,主要是我刚刚开始学习编程,程序效率还很低。
但是从这些数据就可以发现点端倪。对于某一类数,只要它的素因子定了下来,那么它的分拆数变化规律就比较明显了,尤其是对于$k^n$这一类数,其中k是一个偶数。也许以后简单的探究可以是这个方向。
附件:哥德巴赫分拆数表.zip
待续...
转载到请包括本文地址:https://spaces.ac.cn/archives/1727
更详细的转载事宜请参考:《科学空间FAQ》
如果您还有什么疑惑或建议,欢迎在下方评论区继续讨论。
如果您觉得本文还不错,欢迎分享/打赏本文。打赏并非要从中获得收益,而是希望知道科学空间获得了多少读者的真心关注。当然,如果你无视它,也不会影响你的阅读。再次表示欢迎和感谢!
如果您需要引用本文,请参考:
苏剑林. (Oct. 06, 2012). 《哥德巴赫猜想浅谈1 》[Blog post]. Retrieved from https://spaces.ac.cn/archives/1727
@online{kexuefm-1727,
title={哥德巴赫猜想浅谈1},
author={苏剑林},
year={2012},
month={Oct},
url={\url{https://spaces.ac.cn/archives/1727}},
}










最近评论