电偶极子浅探（1）

设想两个带有等量异号电荷的点电荷，它们之间的距离足够小，这样的一个模型被称为电偶极子（electric dipole）。我们研究电偶极子，主要是研究它在力学方面的性质。很多东西都可以用电偶极子来近似描述，比如一个小磁体周围的磁场，还有地球本身也可以近似看做一个偶极子来描述它的磁力情况，以及一些双原子分子的模型也被可以看做一个电偶极子模型，等等。在电偶极子模型中，两电荷的距离足够小，以至于我们忽略了一些关于距离的高次方项，只保留了线性部分，但对于物理探索来说，它已经足够精确，更重要的是，它足够简单，以至于我们可以容易把它清晰地描述出来。

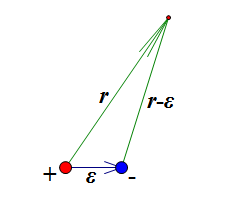
我们先来研究电偶极子产生的电势。设它们各自的电荷量为q和-q，两者距离为ε，根据库仑定律，一个点电荷产生的电势，正比于该电荷的电荷量，同时反比于到该点电荷的距离。那么，一个电偶极子产生的电势为
$U=C(\frac{q}{r}+\frac{-q}{|\vec{r}-\vec{\varepsilon}|})$————(1)

其中$r=|\vec{r}|$，C是一个比例常数。直接用(1)式来研究是比较麻烦的，为此，我们强调了ε是比较小的，因此我们用泰勒级数将它展开来。

$$\frac{1}{|\vec{r}-\vec{\varepsilon}|}=\frac{1}{\sqrt{r^2+\varepsilon^2-2\vec{r}\cdot \vec{\varepsilon}}}$$
$=\frac{1}{r\sqrt{1-2\frac{\vec{r}*\vec{\varepsilon}}{r^2}}}$（忽略了关于ε的平方以上的项）
$$\begin{aligned}=r^{-1}(1-2\frac{\vec{r}\cdot \vec{\varepsilon}}{r^2})^{-0.5} \\ =r^{-1}(1+\frac{\vec{r}\cdot \vec{\varepsilon}}{r^2})\end{aligned}$$

代入(1)式，得到
$$U=-\frac{Cq\vec{r}\cdot \vec{\varepsilon}}{r^3}\tag{2}$$
这是向量形式，我们用极坐标表示，得到一个简洁的形式：
$$U=-\frac{Cq \varepsilon \cos\theta}{r^2}=-\frac{k \cos\theta}{r^2}\tag{3}$$
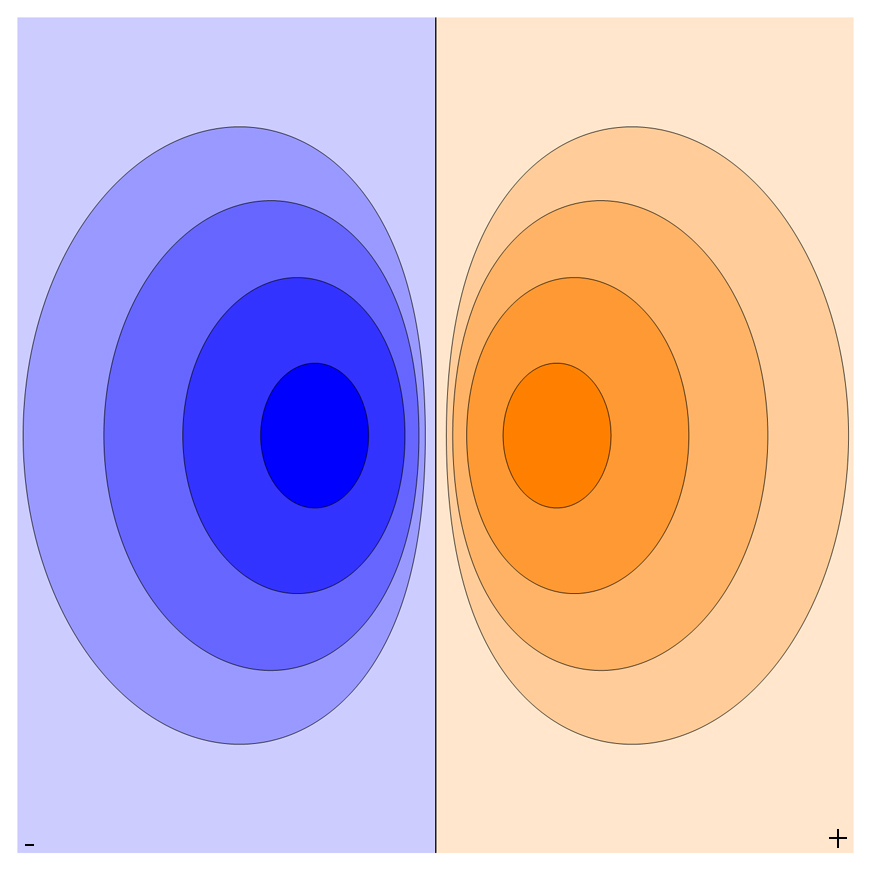
这也就是说，电偶极子的等势面（线）由$-\frac{k cos\theta}{r^2}=const$给出。曲线的形状大概如下：

知道了它的势场，就可以得到它的力场了。从高中的物理就知道，电场线总是与等势面垂直。从数学的角度来讲，那就是
$$E_x=\frac{\partial U}{\partial x},E_y=\frac{\partial U}{\partial y}$$

我们希望求出电场线的轨迹方程，但是我们已知的是势能的极坐标形式。一个有效但是比较麻烦的方法是把U的表达式换回直角坐标形式，然后利用$\frac{dy}{dx}=\frac{E_y}{E_x}=\frac{\partial U/\partial y}{\partial U / \partial x}$来求出电场线的轨迹。下面我们从极坐标角度直接求电场线轨迹。

在极坐标中，对于任意一条曲线$U(r,\theta)=c$，当点从$(r,\theta)$移动到$(r+dr,\theta+d\theta)$时，U的增量为
$$dU=\frac{\partial U}{\partial r}dr+\frac{\partial U}{\partial \theta}d\theta$$

由于U恒等于c，所以上述微分必然会等于0。即
$$\frac{dr}{d\theta}=-\frac{\partial U}{\partial \theta} / \frac{\partial U}{\partial r}\tag{4}$$
我们可以改写成
$$\frac{dr}{rd\theta}=-\frac{\partial U}{\partial \theta} / (r\frac{\partial U}{\partial r})\tag{5}$$
这样改写是因为在我们的印象里，$dr$和$rd\theta$是两个相互垂直的量（微分的基本单元），其作用就是直角坐标系的$dx$和$dy$一样，那么(5)式左端就具有（等势面的）斜率的意义了，而右边就应该是电场力的两个垂直分量之比了。

电场线要求与等势面垂直，那么它的斜率就应该是$-\frac{rd\theta}{dr}$，即电场线的微分方程为
$$-\frac{rd\theta}{dr}=-\frac{\partial U}{\partial \theta} / (r\frac{\partial U}{\partial r})\tag{6}$$
$$\frac{d\theta}{dr}=\frac{\partial U}{\partial \theta} / (r^2\frac{\partial U}{\partial r})\tag{7}$$
将$U=-\frac{k \cos\theta}{r^2}$代入(7)式，就得到
$$\frac{2\cos\theta d\theta}{\sin \theta}d\theta=\frac{1}{r}dr\tag{8}$$
对(8)式两端积分就得到
$$2ln(\sin\theta)+Const=ln r$$

也可以写成$$\frac{\sin^2 \theta}{r}=Const\tag{9}$$
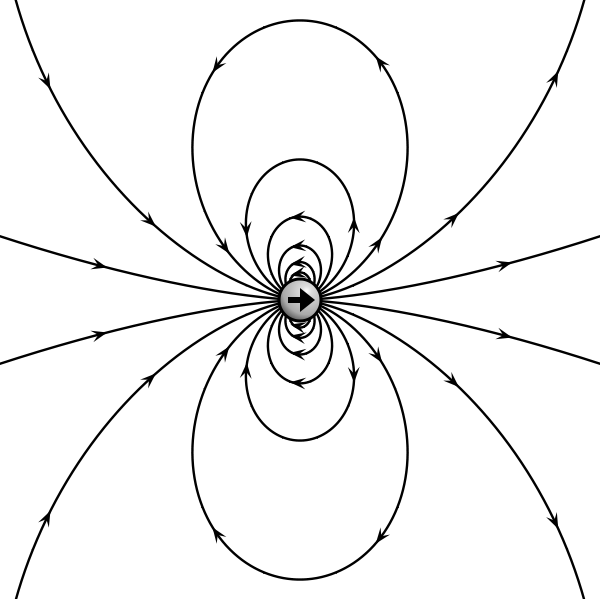
这就是偶极子的电场线方程。其形状大概如图

至此，BoJone对电偶极子的研究已经完成一半了。本文是在《数学桥:对高等数学的一次观赏之旅》的启示之下完成的，但是《数学桥》与本文相关的内容中却有一点叙述不严谨的地方。在《数学桥》中文版278页说到：

在一个偶极子（磁体模型）周围，任何一个带电粒子将沿着下式所代表的曲线运动
$\frac{sin^2 \theta}{r}=k$

但是经过我的验算，带电粒子在电偶极子场中的运动轨迹一般只能够用椭圆积分来描述（这将在下一篇文章说到）；而上式只不过是偶极子的电场线方程而已，一般来说电荷是不会沿着电场线运动的（除非是直线）。这也是一开始让BoJone百思不得其解的地方，现在BoJone在此想“妄下定论”，这是书本的叙述错误，请阅读《数学桥》的朋友们注意一下。当然我没有阅读过英文原著，不能确定是翻译问题还是原著问题。

后一篇文章，我们将会探讨在这样的一个电偶极子场中带电粒子的运动情况。

转载到请包括本文地址：https://spaces.ac.cn/archives/1693

更详细的转载事宜请参考：《科学空间FAQ》